異步電機磁鏈觀測技術的研究

張禮運，張亞東，康樂

(1. 中海油田服務股份有限公司，北京101149；2. 武漢船用電力推進裝置研究所，武漢430064)

0 引言

異步電機運行時電機實際磁場很難通過直接的手段觀測出來，通常采用間接手段觀測異步電機在各種工況下的磁場。但實際電機為非線性系統，存在磁場飽和、磁場交叉影響、參數攝動等因數的影響，這導致基于理想電機的磁鏈觀測模型觀測的磁鏈與電機實際磁鏈在幅值和相位上存在偏差，直接影響異步電機鐵磁材料的利用率（在磁飽和拐點充分利用鐵磁材料），降低了異步電機矢量控制的解耦特性，降低了異步電機的動態性能，嚴重時導致電機無法正常工作。因此，必須采取措施提高異步電機的磁場觀測精度和魯棒性，保證異步電機在任何工況下，觀測磁鏈與實際磁鏈在幅值和旋轉角度上基本保持一致。

目前控制系統中磁鏈觀測模型采取在理想電機數學模型基礎上建模，通過可測量來校正、補償觀測的磁鏈，提高磁鏈觀測的魯棒性、精度[1]。

本文基于異步電機矢量控制系統的磁鏈觀測進行研究與探索。

1 基于異步電機模型下的磁鏈觀測

1.1 電流模型

磁鏈觀測的方法很多，最基本的是從電機理想模型出發得到的電流模型、電壓模型、以及兩者結合的觀測方法。

根據異步電機數學模型得到：

電機存在磁飽和特性和磁場交叉耦合，同時轉子電阻也隨轉子溫度的上升而變化，這限制了電流模型僅能用于低速工況下，且觀測轉子磁鏈幅值和旋轉角度與電機實際轉子磁鏈幅值和旋轉角度有一定的差別。同時定子電流的采樣誤差、控制用的電機參數的誤差也會造成觀測轉子磁鏈幅值與電機實際轉子磁鏈幅值有一定的差別，這些嚴重影響了控制系統性能。

1.2 電壓模型及改進方法

省去繁瑣推導，得到電機電壓模型為：

由于電壓模型中用到了積分環節，帶來積分漂移和積分累積誤差影響實際系統性能。因此需要對電壓模型積分環節作一定處理。

在實際應用中為了減小積分器的直流漂移，抑制低頻噪聲，對積分器進行了改進，常用的解決方案有低通濾波器、磁鏈補償等幾類。

盡管采用串聯低通濾波器能減小漂移，但低通濾波器的時間常數，實際中n一般不會很大，這導致低通濾波帶來的幅值和相位誤差仍然很大。如果濾波器的時間常數是固定值，電機頻率比濾波器頻率低時會產生磁鏈估算誤差，可編程的濾波器方法使濾波器時間常數隨同步旋轉頻率的升高而變小，濾波器的極點在非常低的速度范圍內接近原點，在高速范圍內遠離原點，從而減小低速時磁鏈觀測誤差，但是過大的時間常數會導致直流偏置[2]，所以低通濾波方法存在幅值和相位誤差，故一般采取低通濾波器和一階高階濾波器的結合，對低通濾波器帶來的幅值和相位誤差進行補償。這種積分器磁鏈估計的精度主要依靠限幅的取值。當限幅取值與磁鏈值相等時，效果是最好的。若電機在磁鏈幅值變化（如弱磁模式）情況下運行時，積分器限幅取值也要作相應的調整，這會給實際操作帶來不便。另外由于本方法只是對磁鏈幅值做了補償處理，在磁鏈計算的相位誤差上沒有能很好的改善，導致在帶載接近滿載的時候由于磁場觀測不準而出現過流跳閘。

1.3 電壓、電流混合模型方法

為了解決電壓模型、電流模型在全速范圍內的估計精度問題，可以綜合兩種模型的特點，結合起來使用，在高速時，采用低通濾波器濾除電流模型估計值，在低速時，采用高通濾波器濾除電壓模型估計值，為了實現二者平滑切換，可令高通、低通濾波器二者轉折頻率相等[3]。

原理如下：

電壓模型計算結果輸出轉子磁鏈分量

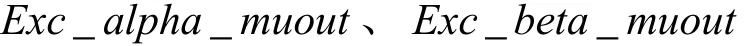
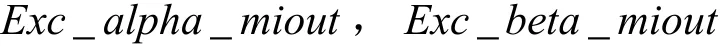
電流模型計算結果輸出轉子磁鏈分量

則輸出轉子磁鏈計算

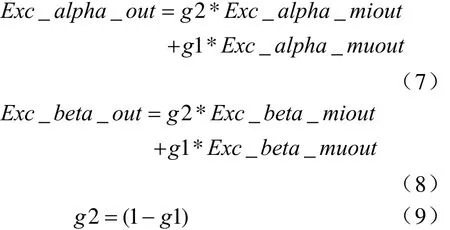
其中g1的確定如圖1所示：

圖1 切換因子g1

計算得到轉子磁鏈分量后，由Exc_alpha_out，Exc_beta_ out計算轉子磁鏈角度的正弦余弦值Sin_fys_mu與Cos_fys_mu，其中混合模型共同作用段為100～500 rpm，切換過程比較平穩，如果混合模型段太短（例如100～150 rpm）容易導致切換時候電流變大，嚴重時導致過流保護。

2 磁鏈閉環觀測

為了增強磁鏈觀測對干擾的抑制能力需要引入各種閉環反饋措施，以增強觀測器的穩定性，并提高狀態估計精度；常見的兩種反饋結構是輸出反饋和狀態反饋，為了實現轉子磁鏈閉環觀測模型，必須以實際電機模型為參考模型，以磁鏈觀測模型為可調模型，當觀測模型與實際某些量發生偏差時（這些量必須是狀態誤差存在時，該誤差就不為0），通過將誤差引入反饋中，最終使二者狀態誤差為0。如圖2所示[5]。

常用的閉環反饋措施有：龍貝格磁鏈觀測器、基于Kalman濾波的磁鏈觀測器。異步電機龍貝格磁鏈觀測器可在不同坐標系下實現磁鏈觀測；根據異步電機數學模型和龍貝格觀測理論，通過引入狀態誤差反饋，可設計轉子磁鏈觀測器，一般采取定子電流和轉子磁鏈作為狀態變量（狀態反饋），也有采取定、轉子磁鏈作為狀態變量的（輸出狀態反饋）。Kalman濾波采用白噪聲為隨機干擾信號和測量噪聲信號建模，必須事先知道誤差和測量噪聲的統計特性，實際系統中只能反復仿真和試驗來選擇合適的參數,比較難以在工程實踐中推廣運用。現對采取定子電流和轉子磁鏈作為狀態變量的龍貝格磁鏈觀測器進行分析。

三相異步電機在旋轉坐標系下的磁鏈和電壓方程分別為[4]：

省去中間過程推導，在進行狀態反饋時由于實際中轉子磁鏈很難觀測到，所以僅采用實際電機定子電流與估算的定子電流差作為狀態反饋量，同時觀測定子電流、轉子磁鏈的全階磁鏈狀態觀測器（輸出反饋），可以用下面公式描述[5]：

通過極點配置的方法得到增益矩陣：

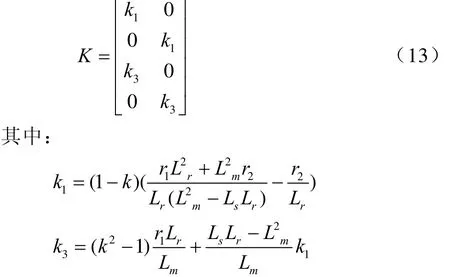
應用中可根據控制精度適當選擇離散算法，離散算法越精確，控制效果越好，但過于復雜的離散算發對硬件資源要求極高。

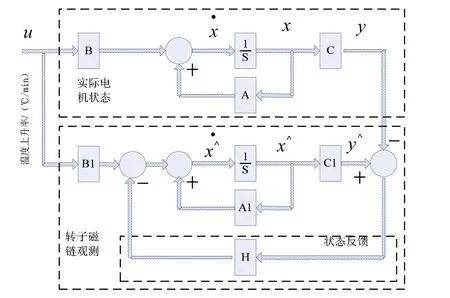
圖2 狀態觀測器及其實現狀態反饋圖

在龍貝格轉子磁鏈觀測模型中，采樣誤差和干擾模型通過電流誤差校正環節輸入到系統中去，這很大程度上提高了系統的抗干擾能力；為保證觀測器的穩定性，其反饋矩陣參數一般通過極點配置方法選取，如果極點離虛軸太近，則觀測器的收斂速度太慢，若極點離虛軸太遠，觀測器對測量噪聲的抑制作用減弱，因此，需要憑經驗不斷調整反饋增益矩陣，以保證觀測器在任何頻率下都穩定，同時收斂速度也滿足要求。

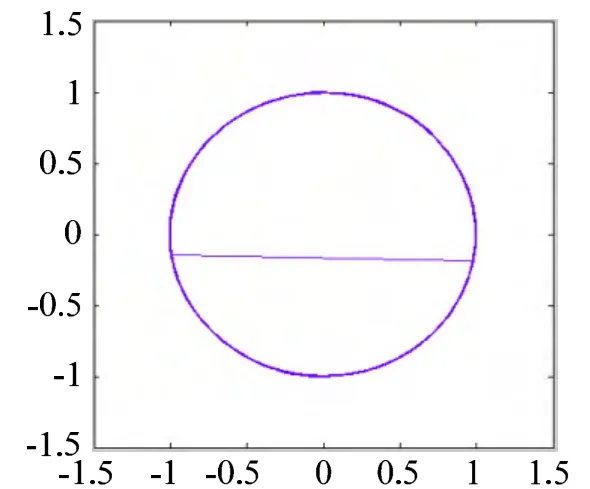
圖3 磁鏈軌跡

3 實驗結果及結論

采用數字離散法，對200 kW異步電機進行實驗驗證：當電機轉速達到800 rpm/m，電機輸出功率為83 kW時觀測到的相關波形如圖4。

本文對異步電機的磁鏈觀測技術進行了論述，首先對磁環開環電流、電壓及混合觀測的數學模型進行分析，然后對閉環磁鏈進行較全面論述，重點對龍貝格轉子磁鏈觀測模型進行理論分析，并通過實驗驗證了該方法的工程使用價值。

圖4 轉子磁鏈α軸與β軸分量

[4]C. G. Hodge, D. J. Mattick. The electric warship[J].Transaction on International Marine Engineering, 108,part2, 1996: 109-125.

[5]劉忠舉, 劉梁寶明等. 基于改進型積分器的矢量控制系統研究. 電力電子技術, 2010, 2: 12-17.

[6]翁海清, 李發海, 劉叢偉. 異步電機降階磁鏈觀測器的研究. 清華大學學報, 2001, 41: 9.

[7]辜承林, 陳喬夫. 電機學. 武漢: 華中科技大學出版社, 2001.

[8]陳堅. 交流電機數學模型及調速系統. 北京: 國防工業出版社, 1989.