T-S模糊系統非脆弱跟蹤控制器設計

程權成，常曉恒

（渤海大學 工學院,遼寧 錦州 121013）

T-S模糊系統非脆弱跟蹤控制器設計

程權成，常曉恒

（渤海大學 工學院,遼寧 錦州 121013）

針對T-S模糊系統，研究了非脆弱H∞跟蹤控制器的設計問題。目的是通過設計跟蹤控制器使得被控閉環系統滿足給定的H∞跟蹤控制性能指標。本文采用線性矩陣不等式（LMI）方法，求解過程不必通過二次迭代的兩步算法，所設計的控制器在一定的加性參數變化情況下,仍能保證系統的漸進穩定性。最后，通過單關節剛性機械臂系統的仿真實驗表明了該方法的有效性。

T-S模糊系統；非脆弱；H∞跟蹤控制；LMI

跟蹤控制作為控制理論活躍的研究領域之一，被廣泛應用于機器人軌跡跟蹤、飛行器軌跡跟蹤、高精度機械加工等領域。實現系統的穩定和跟蹤是控制理論的兩類典型問題，然而對于非線性系統而言，其跟蹤控制問題比穩定性問題更加復雜。早在1997年，Kung就曾針對離散系統通過反饋線性化方法設計了模糊跟蹤控制器[1]，然而得到的模糊控制器并不能保證非最小相位系統的穩定性。Lam研究了連續模糊系統的模型跟蹤控制問題，在假定狀態變量可測的前提下，分析了模糊控制器設計的魯棒性問題[2]。為解決[1]中可能存在的不穩定性和[2]中狀態變量不可測時的局限性，Tseng針對T-S模糊模型提出了對于所有輸入有界參考信號的跟蹤控制性能指標，不必通過反饋線性化和復雜的自適應算法便可達到系統性能要求[3]，但其研究的T-S模糊模型中并沒有考慮實際系統中可能存在的不確定性，于是Mansouri在Tseng的研究基礎上用含有不確定性的T-S模糊模型來描述非線性系統[4]，增強了系統的魯棒性。在控制方法和控制性能指標上也有很多改進[5-7]，這些方法均為跟蹤控制問題提供了更加寬泛的理論分析方法。綜上所述，目前針對復雜模糊系統模型設計的跟蹤控制器，需要通過二次迭代的兩步算法或其他復雜算法進行變換求解，不僅增加了系統的保守性，而且降低了系統的時效性。同時，以上關于跟蹤控制器及觀測器的研究中均未考慮非脆弱控制問題[8]。因此，本文通過設計非脆弱跟蹤控制器使得被控閉環系統滿足給定的H∞跟蹤控制性能指標，所設計的控制器考慮存在一定的加性參數變化，控制器的存在條件以線性矩陣不等式（LMI）的形式表示，避免了二次迭代的兩步算法，可行性更高。

1 問題描述

考慮如下的連續T-S模糊系統：

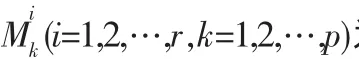
為指定預定軌跡，考慮參考模型如下：

其中，xr(t)∈Rn為參考狀態變量，r(t)為有界參考輸入變量，Ar為穩定矩陣。

選取模糊非脆弱觀測器和控制器的整體模型為：

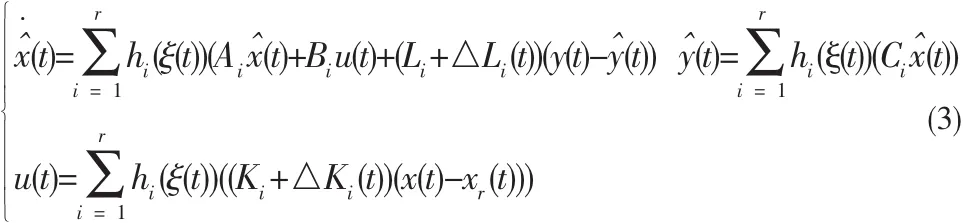
如果不考慮初始狀態，采用與跟蹤誤差y(t)-yr(t)相關的H∞跟蹤控制性能指標如下[7]：

其中，Q為正定的加權矩陣，γ為給定的性能衰減指標。

為推導本文的結果，將用到如下引理：

引理 1[9]：對于任意的矩陣 Xi，i=1,2,…,r和矩陣 S＞0，可

引理2[10]：如果下述兩個矩陣不等式條件成立

引理 4[12]：對于給定適當維數的實矩陣 W=WT，H，E和△T(t)△(t)≤I，那么對于任意常數 σ＞0有：W+H△(t)E+(H△(t)E)T≤W+σ-1HHT+σETE

2 H∞跟蹤控制器設計

本節基于線性矩陣不等式方法，給出了非脆弱 H∞跟蹤控制器及觀測器的存在條件。定理1考慮閉環系統（4），對于給定的 γ＞0，如果存在矩陣 X＞0，Y＞0，P1＞0，P2＞0，P3＞0，，和正常數 σKij，σLij，i，j=1,2…，r使得下述矩陣不等式成立:γii＜0，Γii＜0，i=1，2，…，r γij+γji＜0 Γij+Γji＜0 i，j=1,2，…，r，i＜j

證明：定義 Lyapunov 函數,V(ψ(t))=ψT(t)Pψ(t),P＞0 (6)

代入系統（4），由引理1可知下式成立

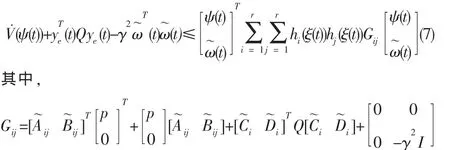
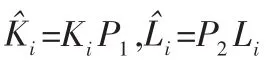
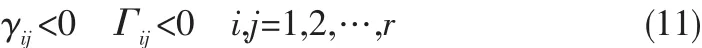
其中，γij，Γij的形式同定理 1。

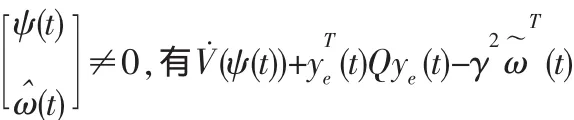
3 仿真實例

為證明提出方法的有效性，考慮如下的單關節剛性機械臂系統[13]：

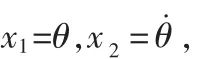
選取參考模型如下：

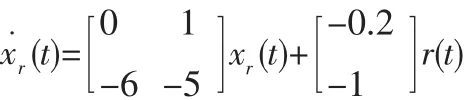
假定跟蹤控制器和觀測器中的不確定參數形如：HK1=-0.1,HK2=0.1,EK1=[-0.1-0.1],EK2=[0.3-0.2],HL1=[-0.3-0.4]T,HL2=[-0.1 0.5]T,EL1=0.1,EL2=-0.6。考慮Q=I時，通過Matlab LMI工具箱求解定理1中的矩陣不等式條件，解得g=7.764時，控制器參數為：K1=[3.134 6-0.871 2]， K2=[-3.268 2-0.834 9]，L1=[-29.573 8 10.027 3]T，L2=[-23.348 7 8.070 4]T。當觀測器和控制器的內部擾動為△Ki(t)=△Li(t)=cos(t)，系統的測量噪聲為v(t)=[exp(-0.1*t)0]T，得到圖1的仿真結果。

圖1 輸出變量y(t)與參考信號輸出變量yr(t)響應曲線Fig.1 The responses of output variable y(t)and reference output variable yr(t)

4 結論

文中針對T-S模糊系統，研究了H∞跟蹤控制器的設計問題，所設計的控制器考慮了加性參數變化的存在。本文的結果以線性矩陣不等式（LMI）的形式給出，求解過程不需要二次迭代，通過該方法求得的跟蹤控制器能夠滿足給定的性能指標。最后，利用對單關節剛性機械臂系統的仿真實驗證明了提出方法的有效性。

[1]Kung C C,Li H H.Tracking control of nonlinear systems by fuzzy model-based controller[C]//Proceedings of the 6th IEEE International Conference on Fuzzy Systems,Barcelona:[s.n.].1997:623-628.

[2]Lam H K,Leung F H F,Tam P K S.Fuzzy control of a class of multivariable nonlinear systems subject to parameter uncertainties:model reference approach[J].International Journal of Approximate Reasoning,2001,26(2):129-144.

[3]Tseng C S,Chen B S,Uang H J.Fuzzy tracking control design for nonlinear dynamic systems via T–S fuzzy model[J].IEEE Transactions on Fuzzy Systems,2001,9(3):381-392.

[4]Mansouri B,Manamanni N,Guelton K,et al.Output feedback LMI tracking control conditions withcriterion for uncertain and disturbed T–S models[J].Information Sciences,2009,179(4):446-457.

[5]Lin T C,Wang C H,Liu H L.Observer-based indirect adaptive fuzzy-neural tracking control for nonlinear SISO systems using VSS andapproaches [J].Fuzzy Sets and Systems,2004,143(2):211-232.

[6]Guo X G,Yang H.output tracking control for delta operator systems with insensitivity to controller coefficient variations[J].International Journal of Systems Science,2011,44(4):652-662.

[7]Lin C,WangQ G,LeeT H.outputtrackingcontrolfor nonlinear systems via T–S fuzzy model approach[J].IEEE Transactions on Systems,Man,and Cybernetics—Part B:Cybernetics,2006,36(2):450-457.

[8]Keel L H,Bhattacharyya S P.Robust,fragile,or optimal[J].IEEE Transactions on Automatic Control,1997,42(8):1098-1105.

[9]Chen C,Feng G,Guan X.Delay-dependent stability analysis and controller synthesis for discrete-time T-S fuzzy systems with time delays[J].IEEE Transactions on Fuzzy Systems,2005,13(5):630-643.

[10]Tseng C S,Hwang C K.Fuzzy observer-based fuzzy control design for nonlinear systems with persistent bounded disturbances[J].Fuzzy Sets and Systems,2007,158(2):164–179.

[11]Boyd S,Ghaoui L E,Feron E,et al.Linear Matrix Inequalities in System and Control Theory[M].Philadelphia:Society for Industrial and Applied Mathematics,1994.

[12]Petersen I R.A stabilization algorithm for a class of uncertain linear system[J].Systems and Control Letters,1987,8(4):351-357.

[13]Pan Y J,Marquez H J,Chen T.Sampled-data iterative learning control for a class of nonlinear networked control systems[C]//Proceedings of the American Control Conference 2006,Minneapolis MN:[s.n.],2006:3494-3499.

Design of non-fragile tracking controller for T-S fuzzy system

CHENG Quan-cheng,CHANG Xiao-heng
（College of Engineering,Bohai University,Jinzhou 121013,China）

According to the T-S fuzzy systems,a non-fragile H∞tracking controller is designed in this thesis.The closed-loop control system can meet H∞tracking performance via the tracking controller that to be designed.The sufficient conditions of controller are obtained via linear matrix inequality (LMI)method.The process of solve without use a two-step iterative algorithm.The designed tracking controller can still ensure the systems are asymptotic stability with some controller parameter perturbations.Finally,the simulation experiment of single-link rigid robot shows the validity of the proposed method.

T-S fuzzy systems;non-fragile;H∞tracking control;LMI

TN964

A

1674-6236（2014）17-001-04

2013-11-12 稿件編號：201311116

國家自然科學基金（61104071）;遼寧省高等學校杰出青年學者成長計劃(LJQ2012095);遼寧省裝備制造綜合自動化重點實驗室開放項目（1120211415）

程權成（1989—），男，遼寧遼陽人，碩士研究生。研究方向：模糊控制、非脆弱控制、跟蹤控制。