非線性電容RLC串聯電路的1/2次亞諧共振分析*

李高峰

(唐山學院唐山市結構與振動工程重點實驗室，河北唐山063000)

非線性電容RLC串聯電路的1/2次亞諧共振分析*

李高峰*

(唐山學院唐山市結構與振動工程重點實驗室，河北唐山063000)

以非線性電容RLC串聯電路為研究對象，運用拉格朗日方法建立了系統的微分方程，應用多尺度法求得1/2次亞諧共振的一次近似解并進行數值計算。分析電阻、電感、電容和電動勢對幅頻響應曲線的影響。結果表明，電阻可以抑制振幅值，電動勢可以增大振幅值。電阻增加后電流減弱，非線性也就變弱。運用MATLAB的Simulink工具，對RLC串聯電路系統進行仿真。

RLC電路;非線性電容;多尺度法;1/2次亞諧

非線性電抗，如變容二極管，在許多領域的電氣工程已經使用范圍廣泛。在設計參數放大器、上頻器、混音器、低功率微波振蕩器、電子調諧裝置等電路時，非線性電容可作為其中的一部分。非線性元件電路是指由非線性元件構成的電路，如線圈、電容等構成的 LR，CR，LC，RLC(Resistance Inductance Capacitance)電路等。詹士昌用普通鎢絲燈泡、變壓器線圈和電容組成的非線性RLC串聯鐵磁諧振電路［1］。王小艷用數值方法對非線性RLC串并聯電路的暫態過程進行了分析研究，得到了非線性RLC電路的一些普遍特征［2］。楊志安研究電阻和電感非線性RLC電路耦合系統的非線性振動，建立受簡諧激勵的具有電阻和電感非線性RLC電路耦合系統的數學模型，根據非線性振動的多尺度法，得到系統滿足共振條件的一次近似解以及對應的定常解［3-6］。崔一輝分別用龍格庫塔法和級數法計算了在無外激勵的情況下，有阻尼和無阻尼時系統分別對應的時間響應［7］。常秀芳從分析實際問題入手，依據閉合電路定律，從中建立RLC振蕩電路的數學模型［8］。Homsup N和Homsup W利用Newton-Raphson迭代法證明直流非線性電路在穩態模擬狀態下是慢收斂的［9］。Blankenstein G通過混合勢函數描述考慮不受約束的控制電壓或電流源非線性RLC電路動力學問題［10］。Chakravarthy S K研究了具有spurious energisation特征的電路非線性振動［11］。AliOksasoglu和 Dimitry Vavriv研究了RLC電路在弱非線性激勵下，適當的系統參數也能使系統產生混沌現象［12］。

電工中常利用某些元器件的非線性。例如避雷器的非線性特性表現在高電壓下電阻值變小，這性質被用來保護雷電下的電工設備;鐵心線圈的非線性由磁場的磁飽和引起，這性質被用來制造直流電流互感器。音頻信號發生器的自激振蕩電路中因有放大器這一非線性元件而成為非線性電路。

本文的非線性電容是電荷控制型，以非線性電容RLC串聯電路振動方程為基礎，研究電路的1/2次亞諧共振［13］問題。

1 RLC串聯電路的振動方程

圖1給出RLC串聯電路，電阻R、電感L、電容C和電動勢u(t)=Emcos(ωt)串接，具有阻尼力和電場力作用。電路中的電容是非線性電容，庫伏特性為u(q)=…。由此可知，RLC串聯電路是非線性系統。

圖1 非線性RLC串聯電路

拉格朗日方法是用廣義坐標，從能量的觀點研究系統的動力學問題。圖1電路取電荷q為廣義坐標，則電流i=q˙，系統的磁能為。庫伏特性僅取3次方，由此可得電容器的電能，系統的拉格朗日函數La=Wm-We。

根據拉格朗日-麥克斯韋方程，可得到該系統的運動微分方程為

進一步得

對式(1)進行處理，可得著名的達芬(Duffing)方程為

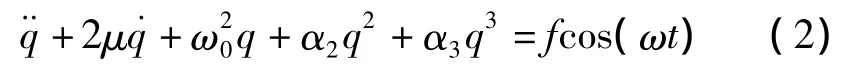
2 1/2次亞諧共振理論分析［13］

系統的阻尼力、非線性力與慣性力和線性力相比是小量，所以在它們前面冠以小參數ε，利用多尺度法求解式(2)，首先引入時間尺度T0=t，T1=εt，ε是小參數，則有微分算子

設1/2次亞諧共振的一次近似解為

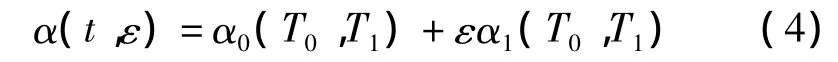
將式(4)代入式(2)，比較ε同次冪的系數得

方程(5)的通解為

將式(7)代入式(6)得

符號NNT為共軛復數項。

研究系統的1/2次亞諧共振［13］，引入調諧參數σ，由下式確定:

消除共軛復數條件為

由式(4)得相應的一次近似解為

式中a和φ由式(11)給出。

令D1a=0，D1φ=0，兩式平方相加得到:

產生上述1/2亞諧共振的原因是Duffing系統具有平方非線性。這種高頻激勵誘發低頻共振的現象在工程中屢見不鮮。例如，1956年，Lefschetz報道一架飛機的螺旋槳激發出機翼的1/2次共振，機翼共振又激發了尾翼的1/4次共振，以致飛機被破壞。避免上述危險是研究非線性振動的目的之一。

3 1/2次亞諧共振數值分析

在下面的數值計算中取以下參數:R=400 Ω，Em=10 V，L=30 H，C0=0.000 1 F，由式(13)可以計算系統1/2次亞諧共振的響應曲線，分析不同參數對響應曲線的影響。

圖2是1/2次亞諧共振的幅頻響應曲線，實線的振幅大，漸近穩定，虛線的振幅小且不穩定;隨著調諧幅值的增加，幅值增加最后趨于穩定。圖2(a)為3種不同電動勢的幅頻響應曲線，隨著電動勢的增加，系統的共振區間增大，但共振幅值減小。圖2(b)為2種不同電阻的幅頻響應曲線，隨著電阻的增加，系統的共振區域減小，共振幅值的上邊曲線下移，下邊曲線上移，向里邊瘦了一圈。這是由于電阻增加后電流減弱，非線性也就變弱的緣故。由圖2(c)知隨著電感增加，系統幅值增加的越來越快，共振區域減小并向右偏移。由圖2(d)知隨著電容增加，系統的共振區間增大且向左偏移，共振幅值減小了但幅度不大，最終會趨于同一范圍值。圖2(e)和圖2(f)電荷系數是幅頻響應曲線。電荷系數k3不僅影響振動幅值的變化趨勢，還影響共振區域的偏移，這與圖2(c)類似。電荷系數k2只影響共振區域，振動幅值的增長趨勢并無變化，這與圖2(b)類似。由此可知，電動勢、電容、電感的數值的變化對系統共振區間和振幅均可影響系統。

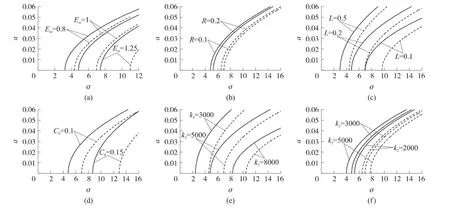
圖2 幅頻響應曲線

圖3 振幅-電動勢響應曲線

圖3為在2種調諧值作用下，隨電動勢變化的振動響應曲線。在有共振響應的范圍內，隨著電動勢的增大，振幅減小，只有在共振區域內才有解。圖4為3種調諧值σ作用下，系統隨電荷系數k2改變的振動響應曲線。在共振響應的范圍內，隨著電荷系數k2的增大，振幅增大;當調諧值σ＞0時，幅頻響應曲線具有跳躍現象和滯后現象;在調諧值σ≤0時，系統振動幅值逐漸增加，趨于穩定，跳躍現象和滯后現象消失。

圖5為2種調諧值σ作用下，系統隨電荷系數k3改變的振動響應曲線。在有共振響應的范圍內，隨著電荷系數k3的增大，振幅減小。圖6為3種調諧值σ作用下，隨電容變化的振動響應曲線。在3組固定參數下均存在最大幅值。在共振響應的范圍內，隨著電容的增大，振幅先增大再減小。

圖4 振幅-電荷系數k2應曲線

圖5 振幅-電荷系數k3應曲線

圖6 振幅-電容響應曲線

圖7為3種調諧值作用下隨系統電感改變的振動響應曲線。當調諧值增加，系統的振動幅值增加，當調諧值σ＞0時，隨著電感的增加系統的振動幅值增大，并趨于穩定。系調諧值σ=20時，圖線由原來的兩只合并成一條圖線。

圖7 振幅-電感響應曲線

圖8為振幅-電阻響應曲線，3組給定調諧參數的響應曲線均存在跳躍現象。調諧值越大系統的振動幅值滯后性越強，逐漸出現了跳躍現象。

由圖3～圖8分析可知，在滿足一定的條件σ≥ 0時，振幅與各個參數之間的響應曲線，也具有跳躍現象和滯后現象，這在非線性系統是很少見的。

圖8 振幅-電阻響應曲線

4 Simulink仿真分析

Simulink是一個用來對動態系統進行建模、仿真和分析的軟件包。它支持線性和非線性系統，連續和離散時間模型，或者是兩者的混合。基于非線性電容的RLC串聯電路的振動微分方程式(2)建立框圖，如圖9。在Simulink的仿真參數選項菜單中選龍格庫塔算法進行數值模擬，通過Scope模塊和XY Graph模塊可以得到位移的時間曲線以及位移和速度的相圖。

圖9 Simulink模型

圖10是模擬時間為2 s和5 s的1/2次亞諧共振時間響應曲線，由圖可知隨著時間的增加電流減小增大交替出現，總體呈減小趨勢，最后趨于穩定，這說明在開始時電容的放電振動比較大，最后趨于穩定。圖11為模擬時間為2 s和5 s的1/2次亞諧共振時的電流與電荷相圖曲線，由圖11可知隨著時間的增加相圖從外向內逐漸收斂，隨著時間的增加系統電流減小，這與數值計算結果是吻合的。

圖10 1/2亞諧共振時間響應曲線

圖11 1/2亞諧共振相位響應相圖

5 結論

建立了基于非線性電容的RLC串聯電路的微分方程，得到1/2次亞諧共振系統的常微分方程。分析了電源、電感、電容等參數變化的影響，得到幅頻響應曲線。電阻對1/2次亞諧共振區有抑制作用;1/2次亞諧共振系統的振幅隨著電動勢的增加不斷增大，并且共振區增大。結合實際情況對曲線進行分析，得到一些結論對此類機構的動態設計具有指導意義。振幅與各個參數之間的響應曲線，在滿足一定的條件時，有跳躍現象和滯后現象出現，在非線性系統是很少見的。非線性電容RLC串聯電路有豐富的非線性動力行為。

［1］ 詹士昌，梁方束.RLC電路非線性現象產生機制的研究［J］.杭州師范學院學報(自然科學版)，2002(4):31-33，38.

［2］ 王小艷.非線性RLC電路特性的數字仿真研究［J］.高壓電器，2001(6):52-54.

［3］ 楊志安，崔一輝.非線性電阻電感型RLC串聯電路主共振分析［J］.天津大學學報，2007，40(5):579-583.

［4］ 楊志安，崔一輝.電感非線性RLC電路彈簧耦合系統3次亞諧共振研究［J］.電子器件，2008，(3):988-991.

［5］ 楊志安，賈尚帥.RLC串聯電路與微梁耦合系統1∶2內共振分析［J］.應用力學學報，2010，27(1):80-85，225.

［6］ 楊志安，賈尚帥.RLC串聯電路與微梁耦合系統的吸合電壓與電振蕩［J］.應用力學學報，2010，27(4):721-726，850.

［7］ 崔一輝，楊志安.RLC電路彈簧耦合系統的級數解［J］.振動與沖擊，2006，25(4):76-77，108，177.

［8］ 常秀芳，李高.RLC-振蕩電路中的數學模型［J］.山西大同大學學報(自然科學版)，2009，25(1):71-73.

［9］ Homsup N，Homsup W.Unconstrained Optimization Method for Finding DC Operating points of RLC Nonlinear Circuits［C］// Modelling and Simulation(MS’99).1999:606-607.

［10］ Blankenstein G.Geometric Modeling of Nonlinear RLC Circuits［J］.IEEE Transactions on Circuits and Systems.Ⅰ.Regular Papers，2005，52(2):396-404.

［11］Chakravarthy S K.Nonlinear Oscillations Due to Spurious Energisation of Transformers［J］.EE Proc-Electr Power Appl，1998，145 (6):585-592.

［12］Ali Oksasoglu.Dimitry Vavriv Interaction of Low and High Frequency Oscillation in a Nonlinear RLC Circuit［J］.IEEE Transaction on Circuit and Systems-Ⅰ:Fundamental Theory and Application，1994，41 (10):669-672.

［13］Nayfeh A H，Mook D T.Nonlinear Oscillation［M］.New York:Wiley-Interscience，1979:96-99.

李高峰(1977- )，女，講師，碩士，主要從事非線性動力學研究，ligaofeng0315@163.com。

1/2 Subharmonic Resonance Analysis of RLC Series Circuit with Nonlinear Capacitance*

LI Gaofeng*

(Tangshan College and Tangshan Key Laboratory of Structure and Vibration Engineering，Tangshan Hebei 063000，China)

Aiming at the research object for RLC series circuit with nonlinear capacitance，using Lagrange method to establish the differential equations of the system，the first approximate solution of 1/2 subharmonic resonance of the nonlinear vibration system is obtained by means of the method of multiple scales for nonlinear oscillations.Numerical analyses on the influence of the parameters of inductance，capacitance and electromotive force(emf)on the amplitude frequency response curve are，as follows，that is，with the increasing of resistance，the amplitude and resonant region of the primary resonance decrease and with the increasing of electromotive force(emf)，the amplitude and resonant region of the primary resonance increase.With the increasing resistance，the current is abate，and than the nonlinearity will weaken.The system of RLC series circuit is simulated by using MATLAB Simulink tool.

RLC circuit;nonlinear capacitance;multiple scales;1/2 subharmonic resonance

10.3969/j.issn.1005－9490.2014.02.017

O321;TM503.2

A

1005－9490(2014)02－0249－05

項目來源:河北省自然基金項目(A2009000997);唐山市科技計劃項目(1313021106)

2013-05-28修改日期:2013-06-16

EEACC:1230B