非線性四階多點邊值問題的正解存在性
孔令彬,辛 彤
(東北石油大學 數學與統計學院,黑龍江 大慶 163318)
非線性四階多點邊值問題的正解存在性
孔令彬,辛 彤
(東北石油大學 數學與統計學院,黑龍江 大慶 163318)
研究一類含參數的非線性四階多點邊值問題,當參數屬于一定范圍時,利用常數變易法求得與邊值問題等價的函數,并對它進行上下界估計,同時利用錐不動點定理,證明該四階邊值問題正解的存在性.
四階邊值問題;常數變易法;錐定理;正解
0 引言
近年來,非線性四階邊值問題受到人們的關注,主要應用在物理學的流體力學、彈性力學等領域問題中,其正解具有深刻意義[1-3].人們研究此類問題,并且得到一些結論[4-9].筆者討論包含參數的非線性四階多點邊值問題,當參數屬于給定范圍時,得出該問題的正解.
1 問題與主要定理
考慮非線性四階多點邊值問題
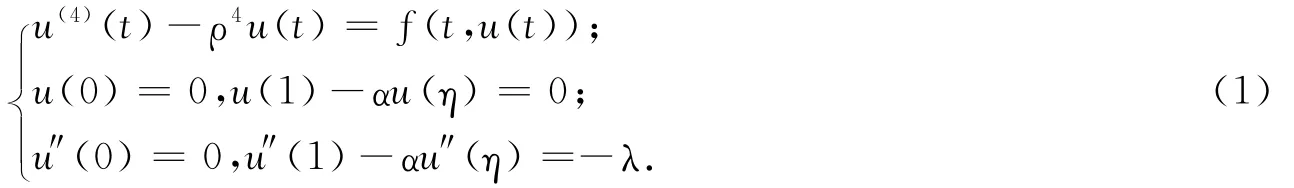
式中:α為正數,0<η<1,滿足αη<1,λ>0;ρ為參數
假設條件成立:
(H1)f(t,u)在[0,1]×[0,+∞)非負連續,且
定義 稱函數u(t)為邊值問題式(1)的正解,如果它滿足u∈C3[0,1]∩C4[0,1],在(0,1)內u(t)>0,并且u(t)滿足式(1).
定理1 假設條件(H1)、(H2)成立,或者條件(H1)、(H3)成立,則所求非線性四階多點邊值問題式(1)有正解.
2 所求問題式(1)的Green函數
引理1 設m、n、q為實常數,φ1(t)、φ2(t)為非奇次方程mv″(t)+nv′(t)+qv(t)=h(t)的2個無關解,φ0(t)是邊值問題,即的一個解,由非齊次方程通解的結構可以得到,φ(t)=c1φ1(t)+c2φ2(t)+φ0(t)是方程av″(t)+bv′(t)+cv(t)=h(t)的通解,其中c1、c2為任意常數.
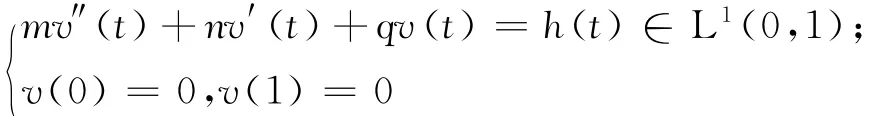
證明 由非齊次方程通解結構直接驗證即可.
先考慮非線性三點邊值問題,即

容易求得非線性邊值問題,即
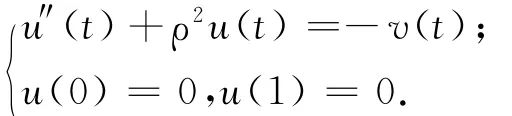
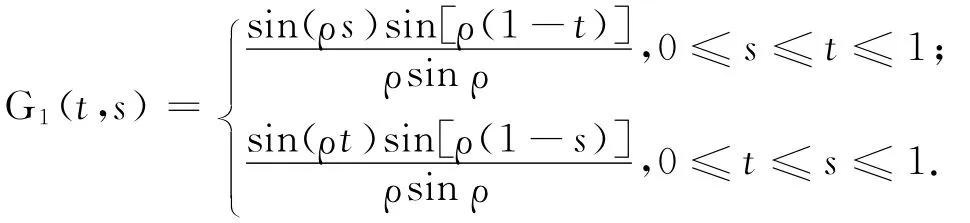
又由于u″(t)+ρ2u(t)=0的2個無關解是φ1(t)=cos(ρt),φ2(t)=sin(ρt),根據引理1知,邊值問題式(2)的通解可以表示為,并滿足初值條件u(0)=0,u(1)=αu(η),利用初值條件可以計算常數c1、c2,經計算整理得邊值問題式(2)的解,用積分方程表達式表示為
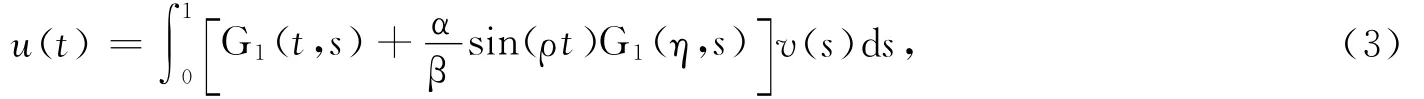
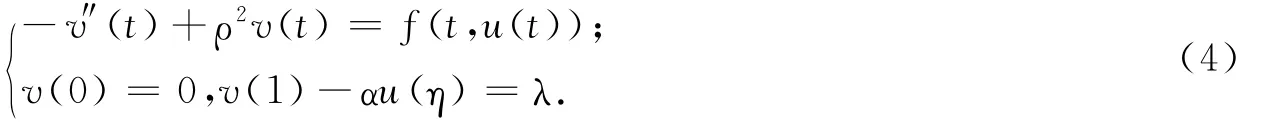
知道非線性邊值問題,即
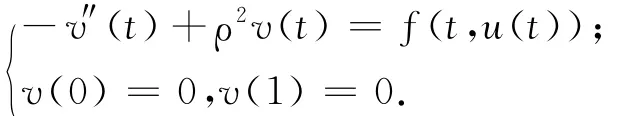
等價于積分方程
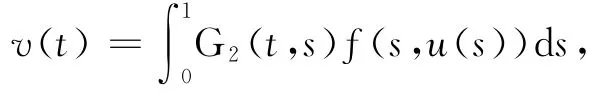
其中
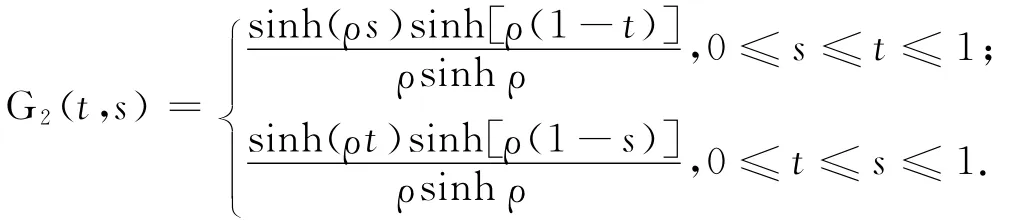
又因為-v″(t)+ρ2v(t)=0的2個無關解是φ1(t)=eρt,φ2(t)=e-ρt.同理,再由引理1知非線性三點邊值問題式(4)的通解可以表示為
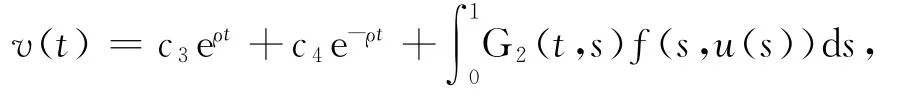
并滿足條件v(0)=0,v(1)-αu(η)=λ,由此確定常數c3、c4,得到邊值問題式(4)的通解等價于積分方程,即
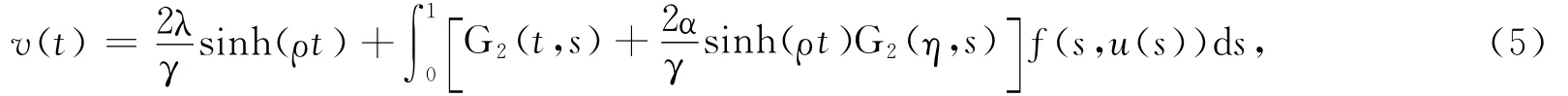
式中:γ=sinhρ-αsinh(ρη)>0.將式(5)代入式(3)并整理可知,非線性邊值問題式(1)的通解為
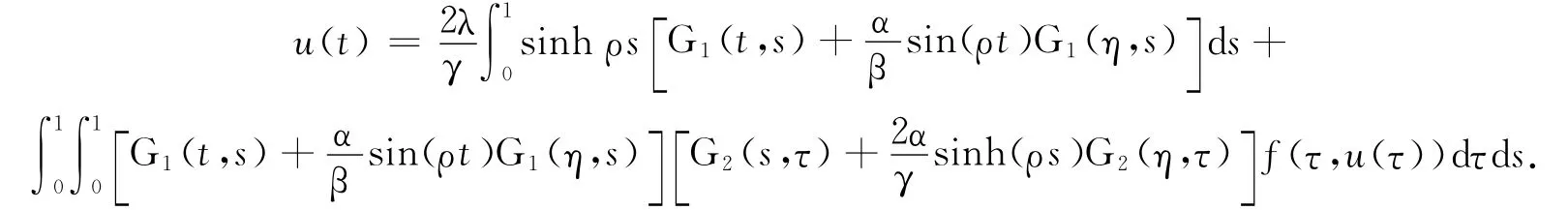
引理2 對于 Green函數G1(t,s)、G2(t,s)滿足:?s,t∈[0,1],成立不等式,即
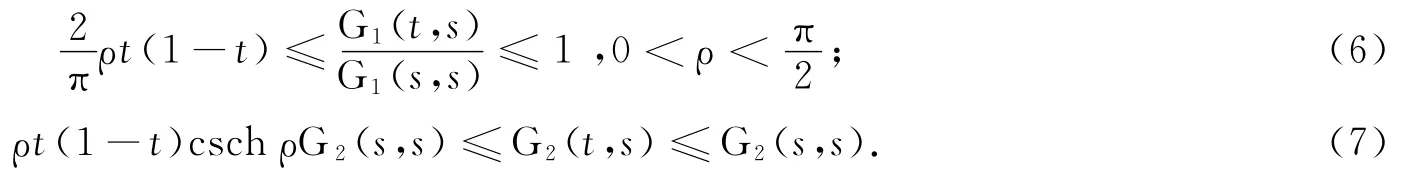
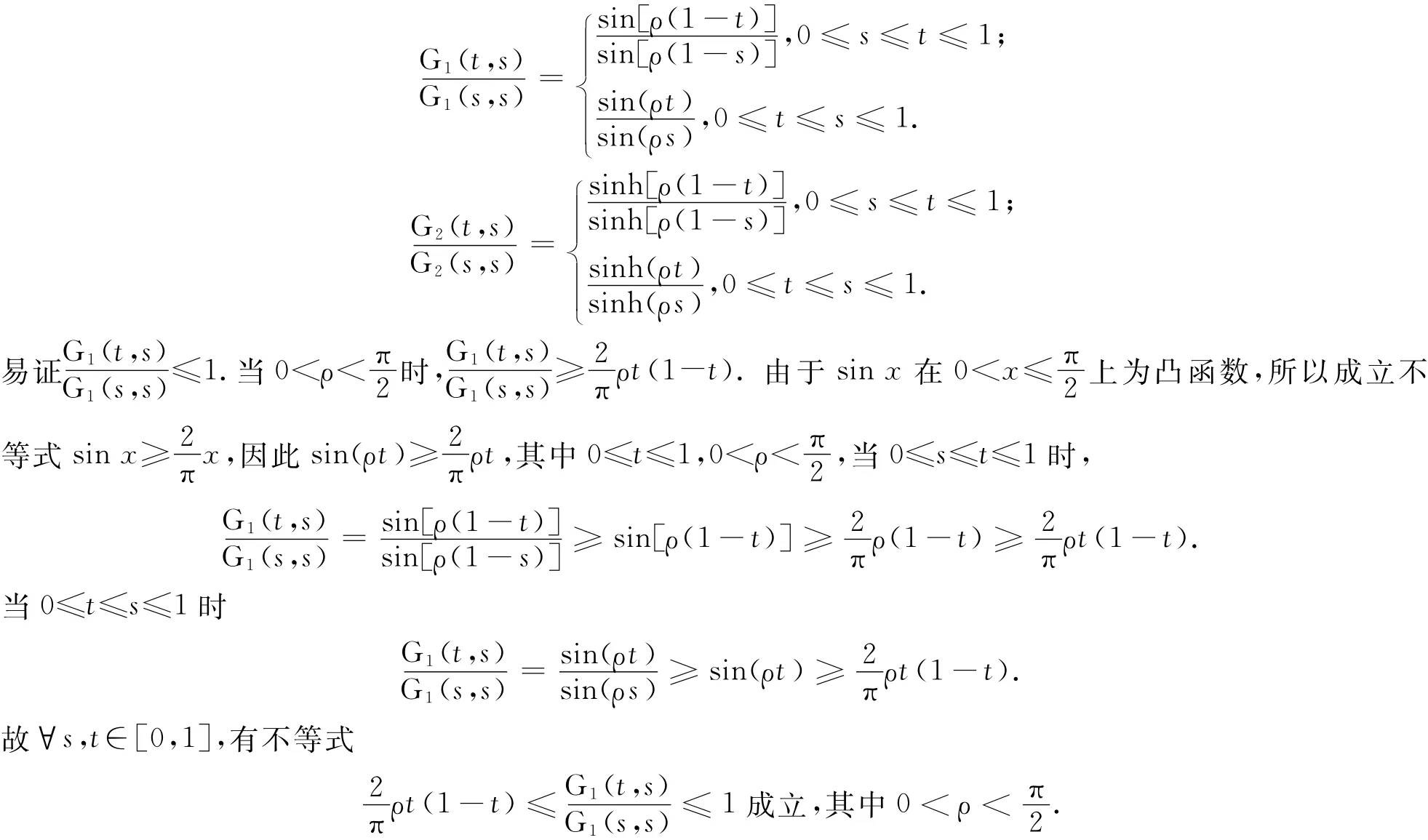
證明 容易得到下列關系利用Taylor公式,并注意到sinh(ρs)的單調性,可知
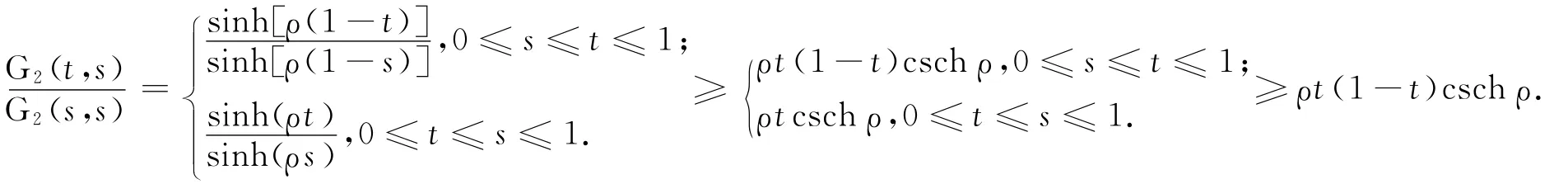
再由sinh(ρs)及sinh[ρ(1-s)]關于s單調性知,因此式(7)成立.
設C[0,1]是[0,1]上全體連續函數構成的Banach空間,C+[0,1]={u∈C[0,1];u≥0},定義映射F:C+[0,1]→C+[0,1],則
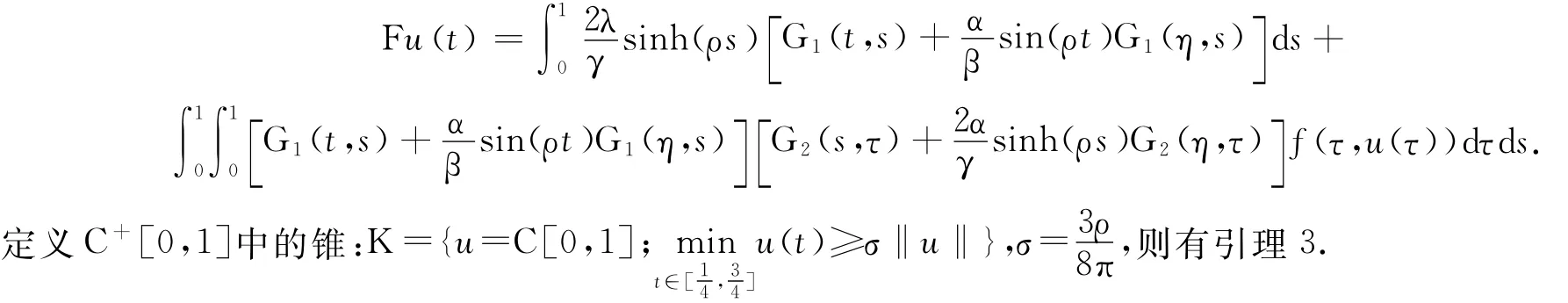
引理3 F:K→K全連續
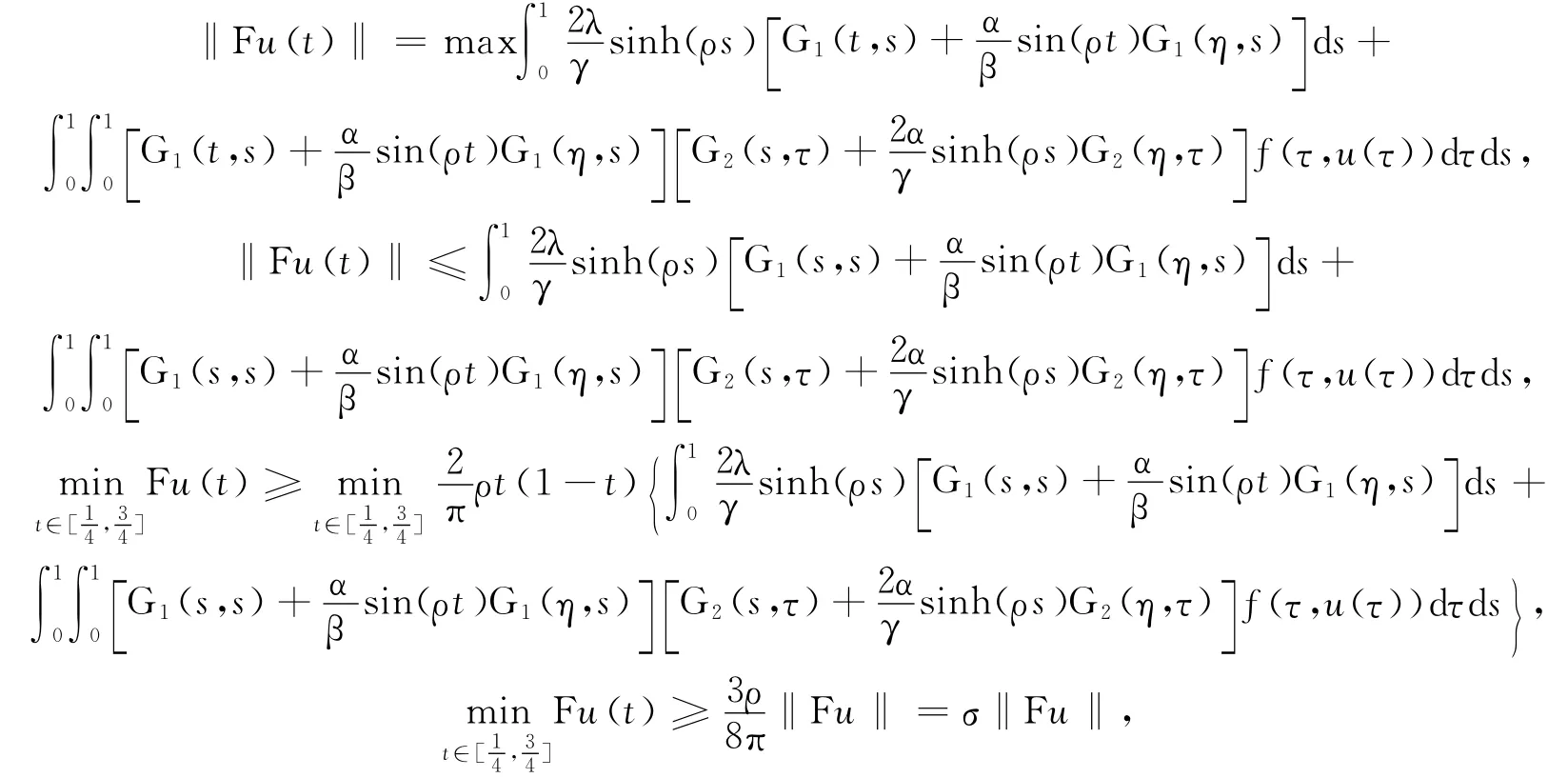
證明 ?u∈K,由引理2知因此Fu∈K,即F(k)?K.另外,容易知道F:K→K全連續映射.
為了證明主要結論,用到錐不動點引理[10].
引理4 設E是Banach空間,K?E是E中的錐,W1、W2是E中的開子集,0∈W1?W2,又設F:K∩W1)→K全連續.如果
(1)‖Fu‖≤‖u‖,u∈K∩?W1,并且‖Fu‖≥‖u‖,u∈K∩?W2;
(2)‖Fu‖≥‖u‖,u∈K∩?W1,并且‖Fu‖≤‖u‖,u∈K∩?W2,則F在K∩(2W1)中至少存在一個不動點.
3 定理1的證明
假設條件(H1)、(H2)成立,則存在λ0∈(0,∞),使當λ∈(0,λ0]時,邊值問題式(1)有正解.記
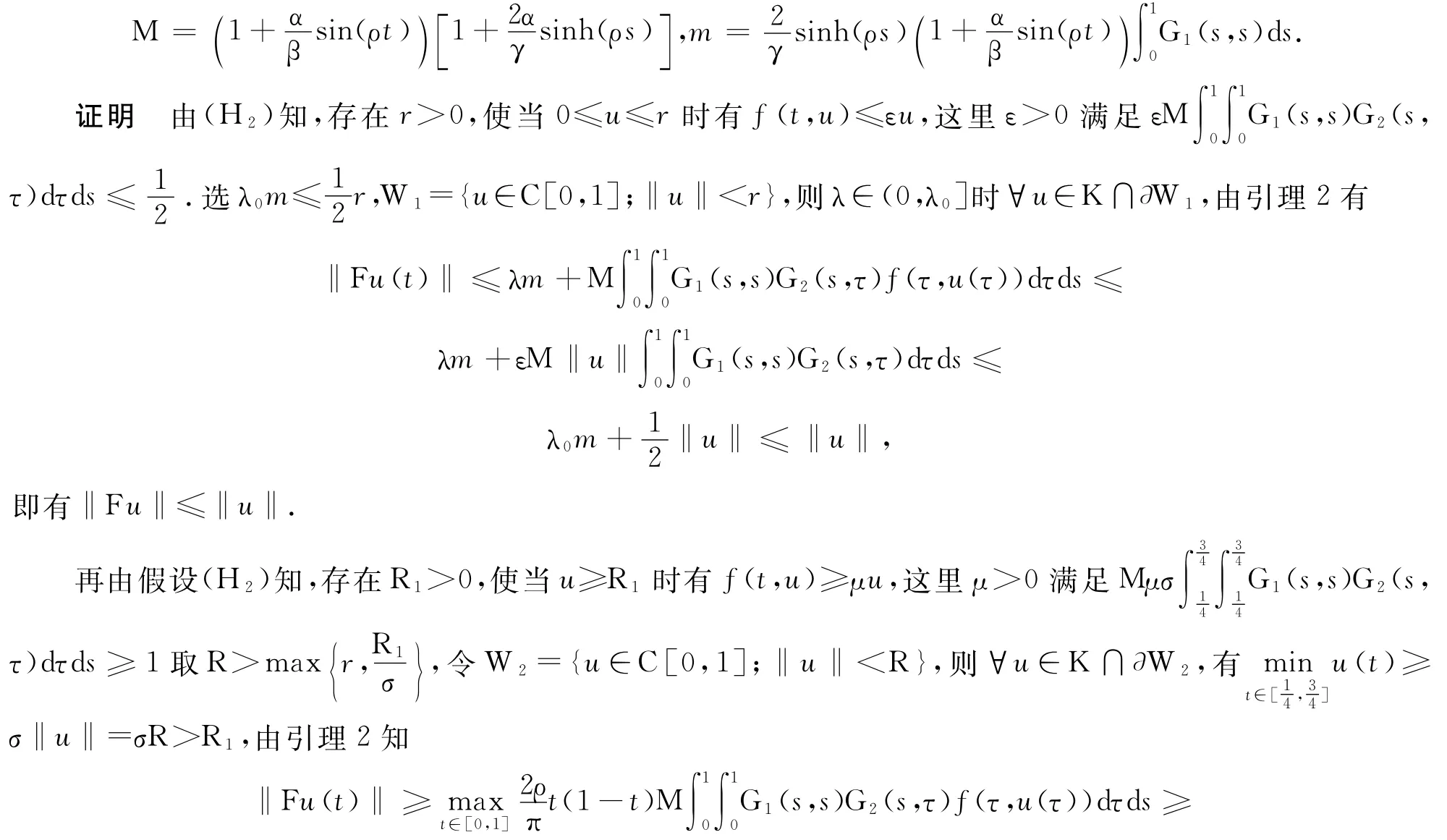
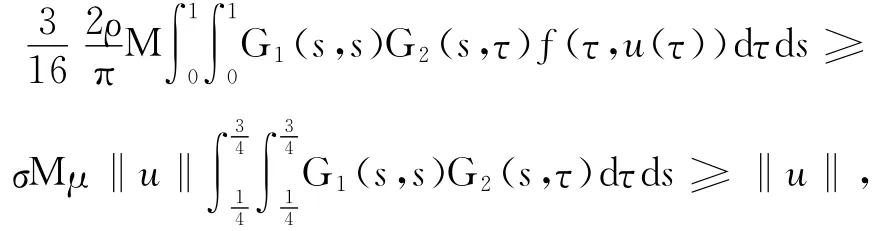
即有‖Fu‖≥‖u‖.
由引理4知,不動點u(t)存在于K∩(ˉW2W1)中,并且滿足Fu=u,因此u(t)是式(1)的一個正解.
假設條件(H1)、(H3)成立.由(H3)知,存在r>0,使當0≤u≤r時,有f(t,u)≥μu,這里μ>0,滿足
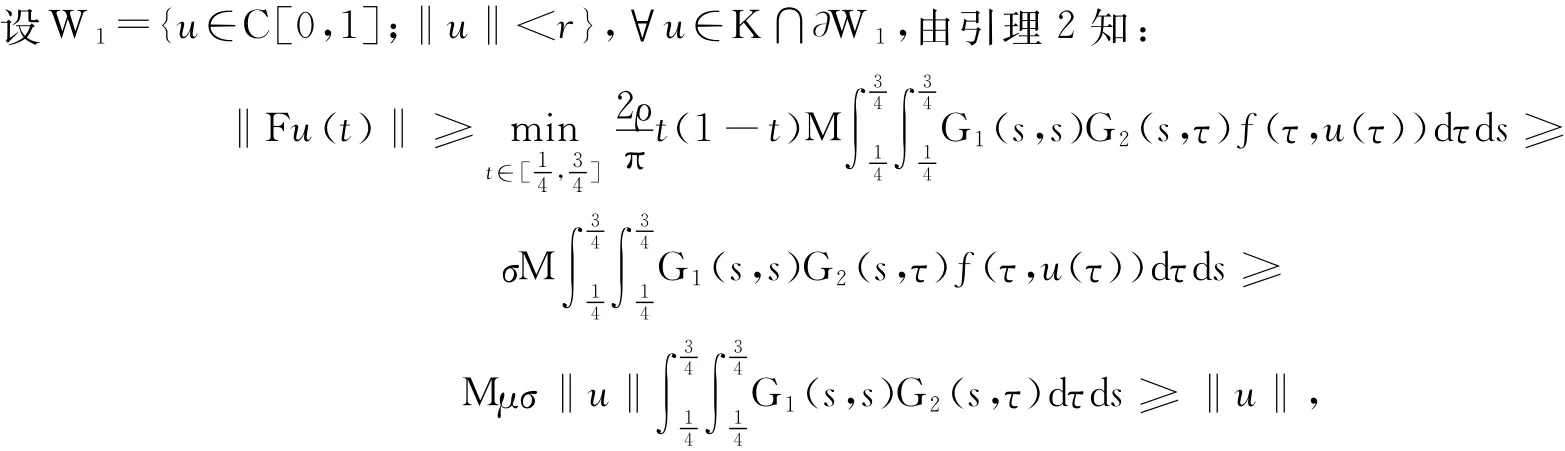
即有‖Fu‖≥‖u‖.
再由條件(H3)知,存在 H>0,使當u≥H 時有f(t,u)≤εu,這里ε>0使,則當λ∈ (0,λ0]時 ?u∈K∩?W1,由引理2知:
(1)若f(t,u)無界,取R>max{r,H}則有?0<u≤R,f(u)≤f(R),令W2={u∈C[0,1];‖u‖<R},則?u∈K∩?W2,有
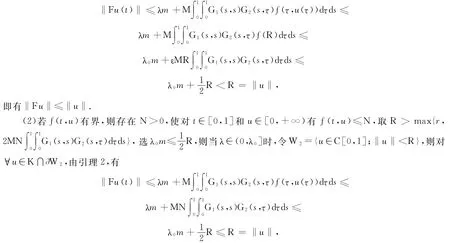
即有‖Fu‖≤‖u‖.
由引理4知,不動點u(t)存在于K∩(ˉW2W1)中,并且滿足Fu=u,因此u(t)是式(1)的一個正解[11-15].
4 結束語
研究一類含參數的非線性四階多點邊值問題,通過適當的變換應用常數變易法,以及結合非線性方程通解的結構,給出該問題的Green函數,因此求出與此問題等價的積分方程形式,并對其建立上下界估計,同時在錐中定義映射和應用錐不動點定理,最終證明該問題的正解存在性.
[1] Gupta C P.Existence and uniqueness theorem for a bending of an elastic beam equation[J].Anal.Appl,1988(26):289-304.
[2] Agarwal R P.On fourth-order boundary value problems arising in beam analysis[J].Differential Integral Equations,1989(26):91-110.
[3] Gupta C P.Existence and uniqueness results for a bending of an elastic beam equation at resonance[J].Math.Anal.Appl,1998(135):208-225.
[4] Gupta C P.Existence and uniqueness results for some fourth order fully quasilinear boundary value problems[J].Anal.Appl,1990(36):169-175.
[5] 孔令彬,張仲毅.奇異非線性四階邊值問題的正解[J].吉林大學學報,2002,40(1):40-43.
Kong Lingbin,Zhang Zhongyi.Positive solutions of singular nonlinear fourth-order boundary value problem[J].Journal of Jilin Unvirsity,2002,40(1):40-43.
[6] 李興昌,趙增勤.一類非共振奇異半正邊值問題正解的存在性[J].高校應用數學學報,2008,23(1):55-60.
Li Xingchang,Zhao Zengqin.Existence of positive solutions of a class of non-resonant singular boundary value problems[J].Applied Mathematics A Journal of Chinese Unvirsity,2008,23(1):55-60.
[7] Ma R Y,Wang H.On the existence of positive solutions of fourth-order ordinary differential equations[J].Anal.Appl,1995(59):225-231.
[8] 郭大鈞.非線性分析中的半序方法[M].濟南:山東科學技術出版社,2000.
Guo Dajun.Nonlinear analysis method of partially ordered[M].Ji'nan:Shandong Science and Technology Publishing Company,2000.
[9] Coster C D,Fabry C,Munyamarere F.Nonresonance conditions for fourth order nonlinear boundary value problems[J].Internat.J.Math.Sci,1994(17):725-740.
[10] 郭大均,孫經先,劉兆理.非線性常微分方程泛函方法[M].2版.濟南:山東科學技術出版社,2005.
Guo Dajun,Sun JIngxian,Liu Zhaoli.Nonlinear functional differential equation method[M].2nd edition.Ji'nan:Shandong Science and Technology Publishing Company,2005.
[11] Jackson L K,Schrader K.Subfunction and third order differential inequalities[J].Differential Equations,1970(8):180-194.
[12] Hartman P.Ordinary differntial equations[M].New York:Wiley,1964:14.
[13] 李永祥.四階非線性邊值問題的正解存在性和多解性[J].應用數學學報,2003,26(1):109-116.
Li Yongxiang.Positive solutions and multiple solutions of nonlinear boundary value problems for fourth-order[J].Journal of Applied Mathematics,2003,26(1):109-116.
[14] Klasen G A.Differential inequalities and existence theorems for second and third order boundary value problem[J].Differential E-quations,1991(10):529-537.
[15] 劉玉玲.一類半正二階三點邊值問題的正解存在性[J].紡織高校基礎科學學報,2006,19(3):256-258.
Liu Yuling.Existence of positive solutions of a class of second-order three-point boundary value problems[J].Basic Science Journal Textile Colleges and Universities,2006,19(3):256-258.
O175.08
A
2095-4107(2014)04-0097-06
DOI 10.3969/j.issn.2095-4107.2014.03.015
2014-04-09;
關開澄
黑龍江省教育廳科學技術研究項目(12541076)
孔令彬(1956-)男,碩士,教授,主要從事非線性微分方程邊值問題的研究.

