一種基于混合誤差梯度下降算法的過程神經(jīng)網(wǎng)絡(luò)訓(xùn)練

許少華，宋美玲，許 辰，朱新寧

（東北石油大學(xué) 計(jì)算機(jī)與信息技術(shù)學(xué)院，黑龍江 大慶 163318）

一種基于混合誤差梯度下降算法的過程神經(jīng)網(wǎng)絡(luò)訓(xùn)練

許少華，宋美玲，許 辰，朱新寧

（東北石油大學(xué) 計(jì)算機(jī)與信息技術(shù)學(xué)院，黑龍江 大慶 163318）

針對過程神經(jīng)網(wǎng)絡(luò)（PNN）單一訓(xùn)練算法自適應(yīng)調(diào)整能力差、缺乏對學(xué)習(xí)性質(zhì)有效控制的問題，提出一種梯度下降與牛頓迭代相結(jié)合的求解算法——混合誤差梯度下降算法.在訓(xùn)練初始階段，基于網(wǎng)絡(luò)訓(xùn)練目標(biāo)函數(shù)，采用梯度下降法進(jìn)行迭代尋優(yōu)，只需計(jì)算目標(biāo)函數(shù)一階導(dǎo)數(shù)數(shù)值公式，復(fù)雜度低且誤差下降快；當(dāng)梯度下降法學(xué)習(xí)效率降低時，引入牛頓迭代法，并將梯度下降法的訓(xùn)練結(jié)果作為初始參數(shù)代入目標(biāo)函數(shù)，使問題轉(zhuǎn)化為求解非線性方程組，不需要一維搜索而提高網(wǎng)絡(luò)訓(xùn)練效率.通過學(xué)習(xí)效率分析自適應(yīng)調(diào)節(jié)兩種算法的切換，直至滿足停機(jī)條件.將其應(yīng)用于時變信號模式分類，實(shí)驗(yàn)結(jié)果表明，該算法較大地提高PNN訓(xùn)練效率.

過程神經(jīng)元網(wǎng)絡(luò)；算法效率；牛頓迭代法；梯度下降法；混合誤差梯度下降算法

0 引言

針對時空維信息系統(tǒng)的建模和動態(tài)信號處理問題，何新貴院士提出和建立過程神經(jīng)元網(wǎng)絡(luò)（Process Neural Networks，簡稱PNN）理論和模型，證明PNN對L2非線性時變函數(shù)的可逼近性、模型的連續(xù)性，以及對連續(xù)時空維系統(tǒng)建模的可計(jì)算性等性質(zhì)[1-2]，為PNN的應(yīng)用提供理論基礎(chǔ).與傳統(tǒng)神經(jīng)網(wǎng)絡(luò)比較，PNN的結(jié)構(gòu)和信息處理機(jī)制有很大不同，網(wǎng)絡(luò)輸入和連接權(quán)等可以為時變函數(shù)，其函數(shù)形式和所含參數(shù)的位置也具有任意性[3-4]，計(jì)算復(fù)雜度高，因此，恰當(dāng)?shù)膶W(xué)習(xí)算法設(shè)計(jì)對于提高PNN建模效率和應(yīng)用泛化能力具有重要影響.

目前，PNN訓(xùn)練采用的方法主要是基于函數(shù)基展開結(jié)合最小均方誤差準(zhǔn)則的學(xué)習(xí)方法[5-6]，以及與進(jìn)化算法相結(jié)合的優(yōu)化算法[7-8].Zhong S S等提出基于小波變換的PNN學(xué)習(xí)算法[9]；Li Ge建立基于混合遺傳算法的訓(xùn)練方法[10]；丁剛分別開發(fā)PNN基于Legendre正交多項(xiàng)式函數(shù)展開和Levenberg-Marquardt訓(xùn)練算法[11]；劉坤等建立一種基于PSO優(yōu)化的PNN建模方法[12]；李欣等提出PNN量子免疫學(xué)習(xí)算法[13-15]等.這些研究結(jié)果豐富PNN的訓(xùn)練方法，提高網(wǎng)絡(luò)模型的應(yīng)用能力，但是單一算法的計(jì)算復(fù)雜度與輸入信號的復(fù)雜性、網(wǎng)絡(luò)規(guī)模呈倍數(shù)增加，待定參數(shù)冗余且自由度大；同時，在訓(xùn)練過程中算法的自適應(yīng)調(diào)整能力差，缺乏對學(xué)習(xí)性質(zhì)的有效控制，在應(yīng)用中對訓(xùn)練樣本集的構(gòu)建也有較高的要求，系統(tǒng)的建模效率也較低.

筆者提出一種基于梯度下降—牛頓迭代相結(jié)合的過程神經(jīng)網(wǎng)絡(luò)混合誤差梯度下降學(xué)習(xí)方法.梯度下降法只需計(jì)算目標(biāo)函數(shù)一階導(dǎo)數(shù)，利用等價(jià)的數(shù)值迭代公式求解時計(jì)算復(fù)雜性小、誤差下降速度快，針對訓(xùn)練目標(biāo)函數(shù)，在網(wǎng)絡(luò)學(xué)習(xí)的初始階段使用梯度下降法[16].當(dāng)梯度下降法學(xué)習(xí)效率降低時，基于網(wǎng)絡(luò)訓(xùn)練目標(biāo)函數(shù)引入牛頓迭代法[17]，并將梯度下降法當(dāng)前的訓(xùn)練結(jié)果作為初始參數(shù)代入目標(biāo)函數(shù)，使問題轉(zhuǎn)化為求解非線性方程組.設(shè)置基于學(xué)習(xí)效率分析的切換條件，兩種算法自適應(yīng)交替使用，在機(jī)制上可有效提高PNN的訓(xùn)練效率.

1 權(quán)函數(shù)基展開PNN模型

考慮一種網(wǎng)絡(luò)權(quán)函數(shù)被一組已知函數(shù)基展開的過程神經(jīng)網(wǎng)絡(luò)模型，它與PNN基本模型[13]具有等價(jià)的信息處理機(jī)制，是在滿足擬合精度要求的前提下，將權(quán)函數(shù)表示為基函數(shù)的有限項(xiàng)展開形式.在應(yīng)用中，只需要根據(jù)非線性時變系統(tǒng)的概率統(tǒng)計(jì)性質(zhì)選擇適當(dāng)?shù)暮瘮?shù)基，即可采用傳統(tǒng)神經(jīng)網(wǎng)絡(luò)已有的成熟學(xué)習(xí)算法進(jìn)行系統(tǒng)建模和網(wǎng)絡(luò)訓(xùn)練.

設(shè)x（t）∈U?Rn，其中，t∈[0，T]，U∈C[0，T]n.為不失一般性，只討論多輸入/單輸出PNN模型，將其結(jié)果容易推廣到多輸出的情況.假設(shè)PNN的權(quán)函數(shù)可被U中的一組有限函數(shù)基B（t）=（b1（t），b2（t），…bL（t））展開，其中L為滿足U中函數(shù)基展開擬合精度的最小項(xiàng)數(shù)，則權(quán)函數(shù)基展開PNN的結(jié)構(gòu)見圖1.

其中，xi（t）為系統(tǒng)輸入函數(shù)，“∫”和“Σ”分別為過程神經(jīng)元的時、空聚合算子，f為作用函數(shù).權(quán)函數(shù)wij（t）用基函數(shù)展開的形式表示，中間各子層的運(yùn)算公式為

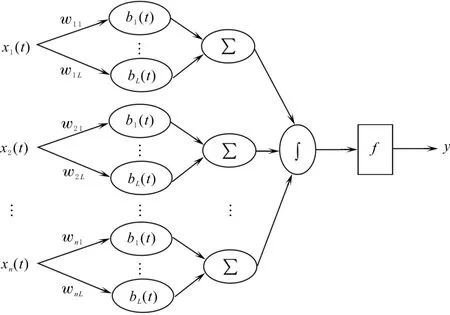
圖1 權(quán)函數(shù)基展開PNN模型Fig.1 Process neural network based on weight function basis expansion

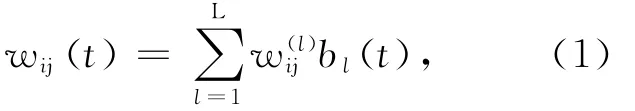
寫成一般映射函數(shù)形式為

若取K（·）為恒等變換函數(shù)，則PNN輸入與輸出之間的映射關(guān)系（見圖1）為

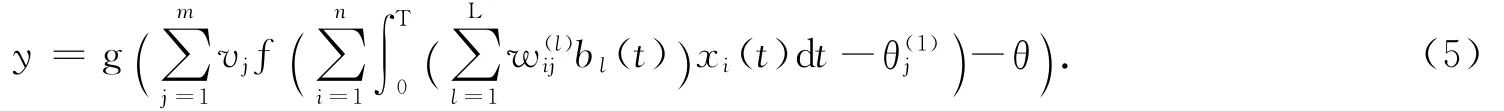
根據(jù)最小誤差準(zhǔn)則，網(wǎng)絡(luò)訓(xùn)練目標(biāo)函數(shù)定義為

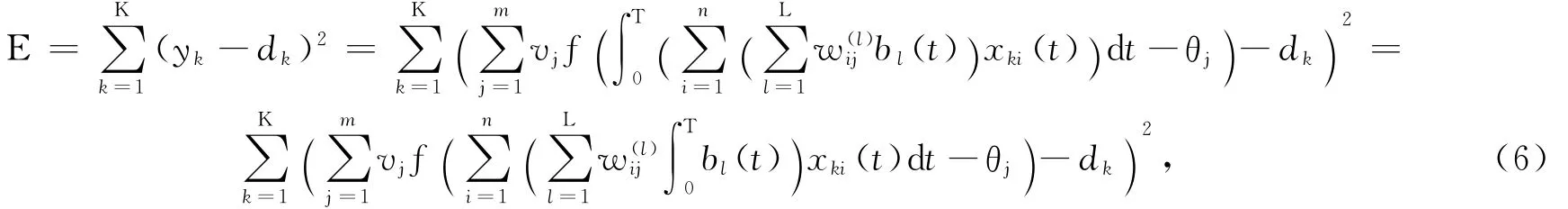
式中：yk為對應(yīng)第k個輸入函數(shù)樣本的網(wǎng)絡(luò)實(shí)際輸出.

2 基于梯度下降—牛頓迭代法結(jié)合的PNN訓(xùn)練算法

2.1 PNN梯度下降算法

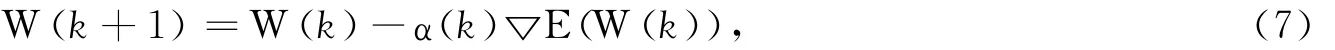
式中：▽E（W（k））為E（W）的一階梯度；α（k）為迭代效率因子

2.2 PNN牛頓迭代算法

在式（6）中，記

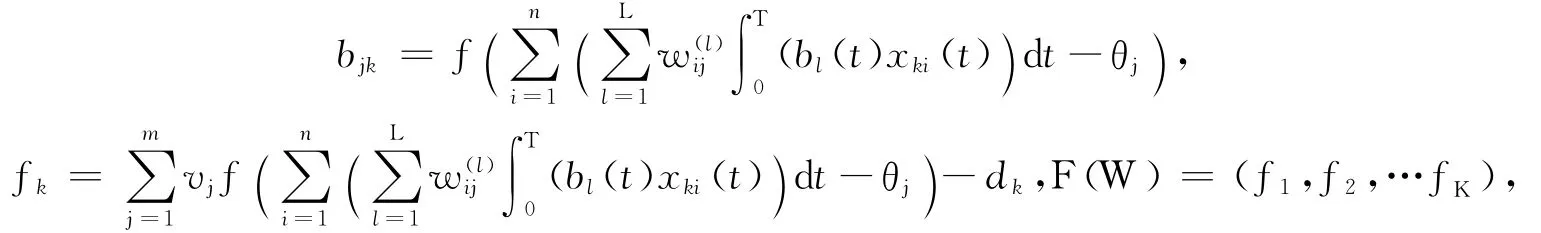
則PNN的求解問題等價(jià)于

式（8）為一個非線性方程組，包含K個方程和n Lm+2m個未知參數(shù).當(dāng)K≤n Lm+2m，且系數(shù)矩陣滿足嚴(yán)格對角占優(yōu)條件時，式（8）存在解.采用牛頓迭代法進(jìn)行求解：

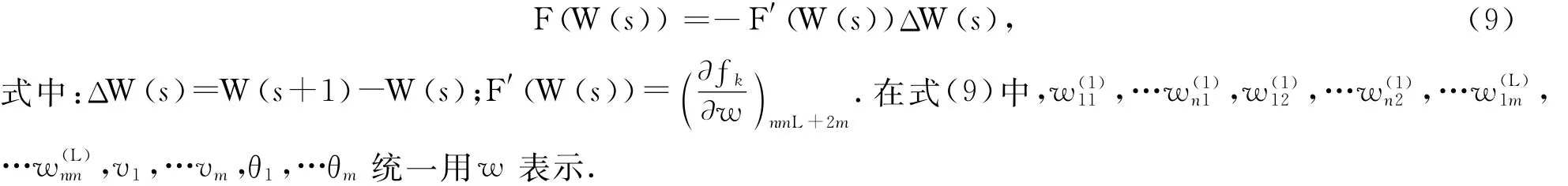
2.3 PNN梯度下降—牛頓迭代訓(xùn)練算法

考慮PNN訓(xùn)練算法的效率，建立梯度下降和牛頓迭代算法的切換準(zhǔn)則：設(shè)θ為效率閾值，ΔL為設(shè)置算法運(yùn)行的迭代間隔，ΔE為經(jīng)ΔL次迭代后E的變化量.若，則進(jìn)行不同算法切換.PNN基于梯度下降—牛頓迭代結(jié)合的混合誤差梯度下降訓(xùn)練算法描述為

Step 1：設(shè)置訓(xùn)練誤差精度ε＞0，最大學(xué)習(xí)步數(shù)M、效率閾值θ和迭代間隔次數(shù)ΔL.

Step 2：執(zhí)行梯度下降法，在[0，1]區(qū)間初始化網(wǎng)絡(luò)連接權(quán)值W（0）.

Step 3：按式（7）進(jìn)行ΔL次循環(huán)迭代，計(jì)算ΔE.

Step 5：若滿足終止條件，則保存目前解停機(jī)；否則，執(zhí)行Step 6，切換到牛頓迭代法.

Step 6：執(zhí)行牛頓法，W 設(shè)置為上一階段算法計(jì)算的結(jié)果；按式（9）進(jìn)行ΔL次循環(huán)迭代，計(jì)算ΔE.

Step 8：若滿足終止條件，保存目前解并停機(jī).

3 實(shí)驗(yàn)分析

采用具有不規(guī)則函數(shù)信號發(fā)生器加噪聲產(chǎn)生3類、60個分段指數(shù)型時變波形信號，函數(shù)的冪指數(shù)和分段區(qū)間在一定范圍內(nèi)隨機(jī)設(shè)定.其中，第1類信號冪指數(shù)取值區(qū)間為[1.0，1.5]，分段區(qū)間長度在[0.9，1.0]內(nèi)隨機(jī)設(shè)定；第2類信號冪指數(shù)取值區(qū)間為[1.9，2.2]，分段區(qū)間長度在[0.8，1.1]內(nèi)隨機(jī)設(shè)定；第3類信號參數(shù)取值區(qū)間分別為[2.9，3.3]和[0.7，1.2].經(jīng)歸一化處理后，構(gòu)成統(tǒng)一的過程信號采樣區(qū)間[0，1].

利用PNN（見圖1）對時變信號進(jìn)行模式分類.對60個信號樣本在誤差精度0.05下進(jìn)行基于Walsh函數(shù)基的展開，當(dāng)基函數(shù)項(xiàng)數(shù)為32時，達(dá)到擬合精度要求.PNN的結(jié)構(gòu)確定為：1-32-1，即1個連續(xù)信號輸入節(jié)點(diǎn)、32個Walsh函數(shù)基節(jié)點(diǎn)、1個時空聚合過程神經(jīng)元輸出節(jié)點(diǎn).隨機(jī)用40個信號函數(shù)構(gòu)成學(xué)習(xí)樣本集，20個信號樣本組成測試集，訓(xùn)練誤差精度設(shè)為0.05.分別用基于正交基展開算法[3]、Fourier函數(shù)變換算法[15]和基于梯度下降—牛頓迭代結(jié)合算法（ΔL=30，θ=0.05）對網(wǎng)絡(luò)進(jìn)行訓(xùn)練，總的迭代次數(shù)均設(shè)定為3 000，每種算法運(yùn)行10次，訓(xùn)練結(jié)果見表1.

表1 3種算法PNN訓(xùn)練結(jié)果Table 1 The results of three train algorithms for PNN

由表1可見，在梯度下降—牛頓迭代結(jié)合算法中，梯度下降法和牛頓迭代法的平均切換次數(shù)為4.6次.梯度下降—牛頓迭代結(jié)合算法，與PNN函數(shù)正交基展開算法訓(xùn)練算法和Fourier函數(shù)變換算法相比，正確識別率基本相同，但學(xué)習(xí)效率有較大提高.這是由于在整個訓(xùn)練過程中實(shí)現(xiàn)兩種算法的自適應(yīng)切換，當(dāng)一種算法略顯停滯時立即切換到另一算法，因而有效實(shí)現(xiàn)兩種算法的優(yōu)勢互補(bǔ).

4 結(jié)束語

提出一種基于梯度下降與牛頓迭代相結(jié)合的過程神經(jīng)網(wǎng)絡(luò)訓(xùn)練算法.該算法將PNN訓(xùn)練的泛函尋優(yōu)轉(zhuǎn)換為對多元函數(shù)求極值的優(yōu)化問題，綜合利用兩種方法不同的求解特性，通過基于效率分析的自適應(yīng)切換策略，實(shí)現(xiàn)網(wǎng)絡(luò)參數(shù)在可行解空間的全局求解.該算法具有明顯優(yōu)于單一算法的收斂速度和逼近能力，對于其他機(jī)器模型的學(xué)習(xí)和復(fù)雜函數(shù)的優(yōu)化等問題的解決具有一定的參考和借鑒價(jià)值.

[1] 何新貴，梁久禎.過程神經(jīng)元網(wǎng)絡(luò)的若干理論問題[J].中國工程科學(xué)，2000，2（12）：40-44.

He Xingui，Liang Jiuzhen.Some theoretical issues on process neural networks[J].Engineering Science，2000，2（12）：40-44.

[2] 許少華，何新貴.關(guān)于連續(xù)過程神經(jīng)元網(wǎng)絡(luò)的一些理論問題[J].電子學(xué)報(bào)，2006，34（10）：1838-1842.

Xu Shaohua，He Xingui.Some theoretical issues on continuous process neural networks[J].Acta Electronica Sinica，2006，34（10）：1838-1841.

[3] 劉顯德，劉立偉，許少華.一種過程神經(jīng)元網(wǎng)絡(luò)模型及其在動態(tài)預(yù)測中的應(yīng)用[J].大慶石油學(xué)院學(xué)報(bào)，2008，32（4）：107-110.

Liu Xiande，Liu Liwei，Xu Shaohua.A process neural networks model and its application to dynamic forecasting[J].Journal of Daqing Petroleum Institute，2008，32（4）：107-110.

[4] 許少華，王皓，王穎.基于過程神經(jīng)網(wǎng)絡(luò)的多維動態(tài)信息處理技術(shù)[J].大慶石油學(xué)院學(xué)報(bào)，2010，34（5）：145-164.

Xu Shaohua，Wang Hao，Wang Ying.Multidimensional dynamic information processing based on process neural networks[J].Journal of Daqing Petroleum Institute，2010，34（5）：145-164.

[5] 許少華，何新貴.基于函數(shù)正交基展開的過程神經(jīng)元網(wǎng)絡(luò)學(xué)習(xí)算法[J].計(jì)算機(jī)學(xué)報(bào)，2004，7（5）：645～650.

Xu Shaohua，He Xingui.Learning algorithms of process neural networks based on orthogonal function basis expansion[J].Chinese J of Computers，2004，27（5）：645-649.

[6] 許少華，肖紅.基于離散Walsh變換的過程神經(jīng)元網(wǎng)絡(luò)學(xué)習(xí)算法[J].大慶石油學(xué)院學(xué)報(bào)，2003，27（4）：58-61.

Xu Shaohua，Xiao Hong.Learning algorithm of process neural networks based on discrete Walsh conversion[J].Journal of Daqing Petroleum Institute，2003，27（4）：58-61.

[7] Kaveh A，Talatahari S.Particle swarm optimizer，ant colony strategy and harmony search scheme hybridized for optimization of truss structures[J].Computers&Structures，2009，87（5）：267-283.

[8] Ababu Teklemariam Tiruneh.Higher order aitken extrapolation with application to converging and diverging Gauss-Seidel iterations[J].Journal of Applied Mathematics and Physics，2013，1（5）：128-143.

[9] Zhong S S，Li Y，Ding G.Continuous wavelet process neural network and its application[J].Neural Network World，2007，17（5）：483-495.

[10] Li Ge，Yin Guisheng.Application of double hidden layer process neural network on wood drying modeling[C]∥Proceedings of 2011 IEEE the 18th International Conference on Industrial Engineering and Engineering Management（Volume 3）.Bejing：Electronic Industry Press，2011.

[11] 丁剛.過程神經(jīng)網(wǎng)絡(luò)泛化能力的理論與應(yīng)用研究[D].哈爾濱：哈爾濱工業(yè)大學(xué)，2008.

Ding Gang.Generalization capability of process neural network and its applications[D].Harbin：Harbin Institute of Technology，2008.

[12] 劉坤，譚營，何新貴.基于粒子群優(yōu)化的過程神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)算法[J].北京大學(xué)學(xué)報(bào)，2011，47（2）：238-244.

Liu Kun，Tan Ying，He Xingui.Particle swarm optimization based learning algorithm for process neural networks[J].Acta Scientiarum Naturalium Universitatis Pekinensis，2011，47（2）：238-244.

[13] 荊獻(xiàn)勇，肖明清，余文波.改進(jìn)免疫算法在預(yù)測過程神經(jīng)網(wǎng)絡(luò)中的應(yīng)用[J].系統(tǒng)工程與電子技術(shù)，2010，32（10）：2136-2140.

Jing Xianyong，Xiao Mingqing，Yu Wenbo.Application of improved immune algorithm in forecast procedure neural network[J].Systems Engineering and Electronics，2010，32（10）：2136-2140.

[14] 葛利.一種基于混合遺傳算法學(xué)習(xí)的過程神經(jīng)網(wǎng)絡(luò)[J].哈爾濱工業(yè)大學(xué)學(xué)報(bào)，2005，37（7）：986-988.

Ge Li.Procedure neural networks based on being learned by hybrid genetic algorithm[J].Journal of Harbin Institute of Technology，2005，37（7）：986-988.

[15] 李欣，程春田.基于過程神經(jīng)網(wǎng)絡(luò)和量子免疫算法的油氣評價(jià)[J].計(jì)算機(jī)工程與應(yīng)用，2008，45（25）：9-13.

Li Xin，Cheng Chuntian.Evaluation method of oil and gas resource based on process neural network and quantum immune algorithm[J].Computer Engineering and Applications，2008，45（25）：9-13.

[16] 關(guān)治，陸金普.數(shù)值分析基礎(chǔ)[M].北京：高等教育出版社，1998.

Guan Zhi，Lu Jinpu.Numerical analysis[M].Beijing：China Higher Education Press，1998.

[17] 王能超.同步并行算法設(shè)計(jì)[M].北京：科學(xué)出版社，1996.

Wang Nengchao.Design of synchronous parallel algorithm[M].Beijing：Science Press，1996.

TP183

A

2095-4107（2014）04-0092-05

DOI 10.3969/j.issn.2095-4107.2014.04.014

2014-03-31；

任志平

國家自然科學(xué)基金項(xiàng)目（61170132）

許少華（1962-），博士后，教授，博士生導(dǎo)師，主要從事人工神經(jīng)網(wǎng)絡(luò)、優(yōu)化算法和可視化數(shù)據(jù)建模方面的研究.