輸電線路的地線不平衡張力計算研究

楊曉梅 張瑞永 吳鎖平

（1.江蘇省電力公司，江蘇 南京210024；2.江蘇省電力設計院，江蘇 南京211102）

0 引言

導地線架線時一般保持耐張段內各檔縱向水平應力相同，受氣溫變化、不均勻覆冰和斷線的作用，各檔的應力將產生不同步變化，直線塔上會出現縱向不平衡張力，嚴重時會造成直線塔倒塔事故，極端條件下的氣象、檔距和高差組合將加劇這種不利影響。

根據文獻［1—3］的研究結論，懸垂串串長越短、檔距越大時，直線塔的覆冰不平衡張力越大，故對于特高壓輸電線路，地線的不平衡張力系數和發生事故概率要大于同條件的導線。對于中、重冰區，文獻［4］給出了地線最大不平衡張力百分數的限值，但工程中桿塔是否超不平衡張力條件，還需通過驗算確定。

由于覆冰不平衡張力的數學模型為高維非線性方程組，隨著地線串長的減小，常規試湊法的計算精度急劇下降，10檔以上計算精度幾乎耗盡；文獻［5］采用信賴域法求解不平衡張力問題，具有較強的魯棒性，但該方法需求解高維Hessian矩陣，工程實現較困難。本文采用逐檔提高迭代精度的方法求解地線覆冰不平衡張力問題，簡單、收斂性好、計算精度高且便于軟件實現。

1 覆冰不平衡張力及斷線張力的計算模型

1.1 應力與檔距增量的關系

假定耐張段內有n個連續檔，考慮補償初伸長而拉緊電線的水平應力為σ0、自重比載為γ0、架線氣溫為t0，采用斜拋物線表達的地線應力σi與檔距增量Δli的關系式為［6］：

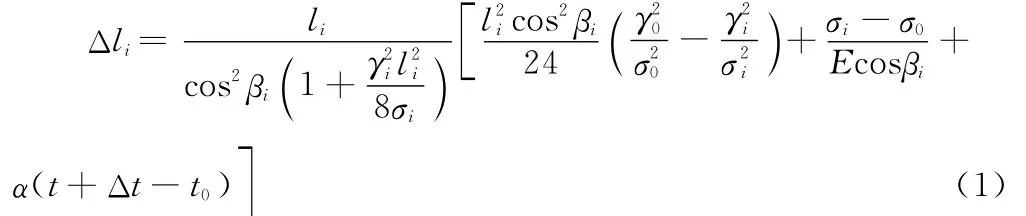
式中，li為第i檔安裝時的檔距（m）；βi為高差角（°）；γi為張力不平衡時第i檔比載［N／（mm2·m）］；E為彈性系數（N／mm2）；α為溫度膨脹系數（1／℃）；t為張力不平衡時氣溫（℃）；Δt為考慮補償初伸長降低的等效溫度（℃）。

1.2 應力的顯式方程

若不考慮懸垂串偏移引起地線懸掛點高差的變化，則根據第基直線塔上懸垂串順線路的水平偏移可求出第i＋1檔應力的顯式方程［6］：

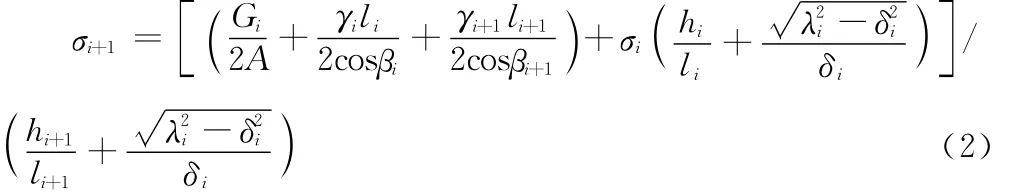
式中，A為地線的計算截面積（mm2）；Gi為懸垂串串重（N）；hi為第i基塔對第i－1基塔地線懸掛點的高差（m）；λi為懸垂串串長（m）。

1.3 不均勻覆冰及斷線的求解條件

在整個耐張段內，不均勻覆冰時檔距增量之和為0，即第n基塔上導線懸掛點的偏距為0：

而當第k＋1檔地線斷線后，地線分為2段：1～k檔和k＋2～n檔。如以1～k檔的斷線不平衡張力進行分析，第k基塔懸垂串承受k檔的垂直荷載和縱向斷線張力，此時有：

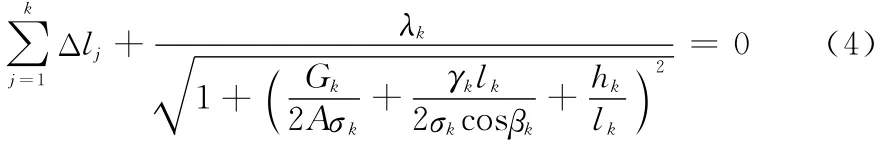
對于地線不均勻覆冰工況，分別以式（1）、（2）和（3）整理出2n個獨立方程求解未知數σi和Δli；對于地線斷線工況，可以式（1）、（2）和（4）整理出個2k獨立方程求解1～k檔的未知數σi和Δli。而對于k＋2～n檔，可采用上述方法逆向求解。

2 逐檔提高迭代精度的實現方法

2.1 計算方法

由于雙精度浮點數僅可表示十進制的15或16位有效數字，而以式（2）采用試湊法求解地線不平衡張力時每次精度損失高達4～50倍，以致難以求出檔數較多、串長較短的地線不平衡張力。采用逐檔提高迭代精度的方法求解地線覆冰和斷線不平衡張力的步驟如下：

（1）令試湊檔l＝1，構造初值σ1、應力下限a、應力上限b：

（2）利用式（2）逐次由i檔計算i＋1檔應力，當｜δi＋1｜≥λi＋1時，利用二分法調整試湊檔的初值σl、應力下限a、應力上限b，重新求解：

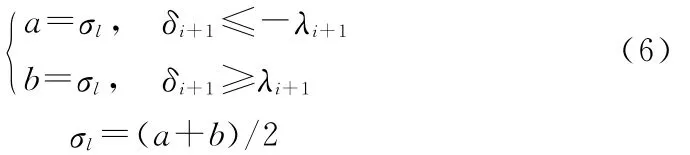
（3）當b≤a＋10eps時，表明試湊檔已接近精度極限，需重新定義下一檔為試湊檔，設置誤差閥值范圍e，構造新試湊檔的應力下限a、應力上限b，重復求解：

通過合理調整e值，可加快收斂速度、提高計算精度，一般可取e＝eps×105，此時應力的計算精度即為e。以上步驟循環求解，直至滿足式（3）或式（4）。

2.2 穩定性驗證

設耐張段含24檔，地線采用LBGJ－170－20 AC鋁包鋼絞線，設計冰厚15 mm，檔距取400 m，前12檔覆冰率20%、后12檔覆冰率100%，高差15%，串重取32.4 kg，張力誤差閥值e取10－12，檔距增量之和的誤差閥值取10－7，地線采用不同串長時，普通試湊法與逐檔提高精度法的收斂性對比如表1所示。

表1 算法收斂性對比

由表1可看出，普通試湊法受迭代精度損失的影響，隨地線串長的減少，檔距增量誤差不斷增大，可計算的檔數也不斷減少，僅通過在第一檔試湊，在極端的檔距、高差和覆冰組合時難以求出地線的不平衡張力；而對于逐檔提高精度的試湊法，當檔距增量之和的誤差大于閥值時，在前一檔試湊求解的基礎上提高下一檔的精度，可輕松完成任意串長的不平衡張力計算。

3 地線不平衡張力計算

3.1 工程條件

浙北—福州1 000 k V輸電線路工程全長2×603 k m，途經浙江和福建歷史上發生過多次較嚴重覆冰斷線、倒塔事故的地區，其中15 mm及以上中、重冰區占70%以上，導地線覆冰不平衡張力較大。全線冰區分布如表2所示。

表2 全線冰區分布

該工程15 mm中冰區單回路導地線分別采用8×JL／G1 A－500／45鋼芯鋁絞線和LBGJ－170－20 AC鋁包鋼絞線。現以該工程某15 mm中冰區耐張段為例，采用逐檔提高精度法進行導地線覆冰不平衡張力及斷線張力的驗算，耐張段斷面如圖1所示。

3.2 驗算結果

按文獻［4］規定，經排列組合驗算，導線不均勻覆冰最大不平衡張力出現在前三檔覆冰率20%、后三檔覆冰率100%時，T4直線塔的不平衡張力最大，驗算結果如表3所示；最大斷線張力出現在第1檔時，T2直線塔的斷線張力最大，驗算結果如表4所示。

由表3和表4可以看出，地線覆冰不平衡張力和斷線張力系數一般大于導線；由于地線斷線張力系數通常不會超過規程的規定值100%，故一般不需再進行直線塔地線斷線的張力驗算；對于覆冰不平衡張力系數，由表3還可以看出，當導線在規程的規定值15%范圍內時，地線卻超出規程的規定值25%，故

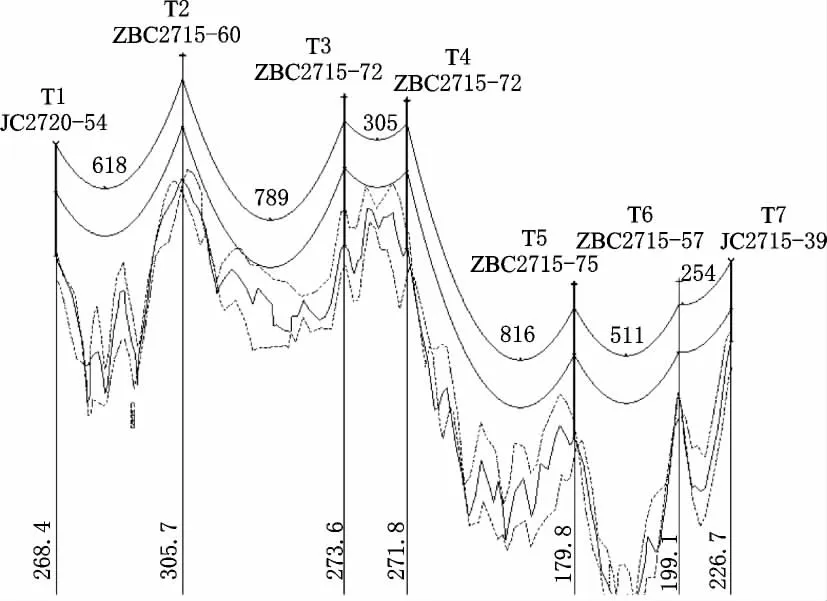
圖1 連續檔斷面圖

表3 導地線覆冰不平衡張力

表4 導地線斷線張力

對特高壓線路覆冰不平衡張力問題，僅進行導線驗算而忽視對地線的驗算是不科學的。

4 結論

（1）逐檔提高精度的不平衡張力計算法具有良好的收斂性，可計算檔距多、串長短的地線不平衡張力，應力計算精度可達，并便于軟件實現；（2）由于地線斷線張力系數通常不會超過規程的規定值100%，故一般不需再進行地線斷線張力驗算；（3）當導線覆冰不平衡張力系數在規程規定值范圍內時，地線也可能超出規程規定值，故有必要加強地線覆冰不平衡張力的驗算。

［1］程思勇，薛志方.覆冰不平衡張力計算分析［J］.電網與清潔能源，2011，27（2）：10～13

［2］呂健雙，李健.特高壓輸電線路覆冰斷線張力計算與分析［J］.電力科學與工程，2013，29（8）：10～15

［3］廖宗高，陳海波，肖立群，等.特高壓輸電線路直線塔縱向不平衡張力取值的探討［J］.電力建設，2006，27（2）：1～3，17

［4］DL／T5440—2009 重覆冰架空輸電線路設計技術規程［S］

［5］薛志方，程思勇.置信域算法在輸電線路覆冰不平衡張力計算中的應用及不平衡張力的影響因素［J］.電網技術，2012，36（4）：225～228

［6］邵天曉.架空送電線路的電線力學計算［M］.第2版.北京：中國電力出版社，2003