燃氣輪機故障診斷中的基準參數計算

林滿山 郭永輝

（北方工業大學信息工程學院，北京100043）

0 引言

在燃氣輪機的故障診斷中，熱力參數的變化量往往可以用來計算燃氣輪機發生故障時的性能變化、判斷故障產生的原因。為了計算熱力參數的變化量，首先需要準確獲得足夠的燃氣輪機無故障狀態下的熱力參數。為了建立燃氣輪機基準模型，目前主要通過大量實驗數據建立燃機仿真模型［1－2］，或者由廠家提供的部件特性曲線和測試數據獲得基準模型的性能參數［3］，也可通過推導氣動熱力學方程獲得數學計算模型［4－5］。然而在實驗成本高昂、發表數據可靠性不強、熱力學方程的推導結果精度往往不夠的情況下，如何綜合使用各種方法，以最小的成本獲得盡可能準確和足夠的性能參數在燃氣輪機故障診斷中有著重要的意義。

本文提出了應用機器學習中的支持向量機理論［6－8］，利用其處理小樣本數據時學習能力強的優勢對有限的燃氣輪機基準運行數據進行學習，從而建立起基準參數計算模型。以某三軸燃氣輪機為例，對文獻［9］中的實際數據進行了建模，結果表明該方法具有很好的適用性。

1 回歸型支持向量機

支持向量機（SV M）是建立在統計學習理論基礎上的一種新的通用學習方法。統計學習理論采用結構風險最小化準則，在最小化樣本點誤差的同時，最小化結構風險以提高泛化能力，且突破了維數的限制。利用支持向量尋求最優分類面，其主要思想是建立一個分類超平面作為決策曲面，使得正例和反例之間的隔離邊緣最大化。

根據相關理論，當SV M用于回歸預測時就是尋找一個最優分類面使得所有訓練樣本離該分類面的誤差最小。設訓練集含有N個訓練樣本｛（x→i，yi），i＝1，2，…N｝，其中，x→i是第i個輸入向量，yi為對應的輸出值。

設要建立的線性回歸函數為：

定義ε線性不敏感損失函數：

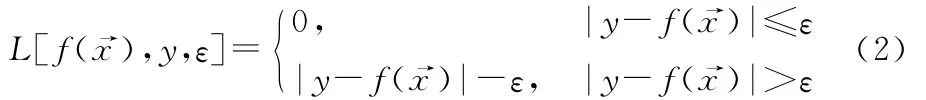
燃氣輪機氣動部分的故障診斷主要是通過壓氣機和透平的性能參數（如流量、效率）變化來判斷故障類型、位置，而實際運行中往往不能直接監測到這些性能參數。這種情況下，就需要建立起可測參數與性能參數之間的關系，通過可測參數得到所需的性能參數。然而燃氣輪機作為一種復雜的先進熱力設備，其熱力參數之間的關系也是高度非線性的，通常的做法是用半經驗公式或非線性多項式進行擬合，通過這些關系式可以得到不同工況下機組的性能參數。雖然這些方法在分析燃氣輪機部件性能、擬合特性曲線方面有一定的適用性，但對特定機組的性能參數進行計算時，其往往需要大量數據才能達到一定的計算精度，因而在燃氣輪機實驗代價及精度要求高的條件下，這些方法略顯局限性。

支持向量機是針對小樣本數據處理提出來的一種新型智能學習算法，對于較少樣本的情況學習能力比較強。本文提出在燃氣輪機基準參數的計算中可利用支持向量機計算所需的性能參數。其基本思路是將影響性能參數的可測參數作為SVM模型的輸入向量，將要求的性能參數作為輸出向量，利用數據樣本對SV M模型進行訓練，得到可用的模型用于燃氣輪機基準參數計算。

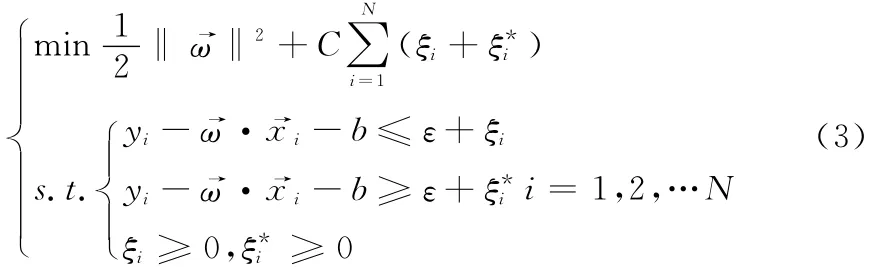
其中，ε規定了回歸函數的精度要求；C為懲罰因子，C越大對訓練誤差大于ε的樣本的懲罰就越大；ξi為松弛變量的上下限，受懲罰因子C的壓制。

實踐中問題往往是非線性的，簡單的分類面無法達到要求，這時需通過非線性映射φ）將原來輸入空間的樣本映射到高維特征空間中，然后在此空間中構造最優分類超平面。定義核函數K（）＝φ（）φ（），以代替原最優分類面中的點積。按照優化理論中的Kuhn－Tucker定理，通過KKT互補條件很容易求解上述拉格朗日函數的對偶問題。支持向量機在建模上表現出很多優勢：針對小樣本，在樣本有限的情況下能獲得最優解；算法最終轉化為二次規劃，理論上可以避免陷入局部最優；良好的泛化能力；能解決“維數災”問題。由于其優異的性能，SV M在各領域得到了廣泛的應用。

2 燃氣輪機基準參數計算

以壓氣機流量計算為例，具體方法如下：（1）構建數據樣本。采集一定量的壓氣機熱力參數樣本從中得到所需的壓比、折合轉速、折合流量等數據。以壓比、折合轉速為樣本集輸入變量，折合流量為輸出變量。（2）數據歸一化處理。即將數據輸入基準化到統一的量綱范圍里，這樣可以避免過大的絕對值輸出誤差的影響，使訓練模擬的范圍相對集中，提高模型計算性能。（3）訓練支持向量機回歸擬合模型。根據支持向量機的基本理論，構建回歸擬合模型需選擇合適的核函數以及參數組合。支持向量機的核函數有很多，本文采取徑向基（RBF）核函數此核函數預測精度比較好。設定精度ε的值后，利用交叉驗證的方法尋找懲罰因子C和核函數中方差σ的最佳組合。用數據樣本對支持向量機進行訓練，得到可用的支持向量機模型。（4）模型計算。利用得到的SVM模型，輸入一定的壓比、折合轉速，便可得到相應模型計算所得的折合流量。同理，利用這種建模方法可建立壓氣機效率、透平流量、透平效率等性能參數的計算模型，進而得到所需的各種工況下的基準性能參數。

3 仿真模擬

以某型三軸燃氣輪機的壓氣機部分為例對上述方法進行驗證，在Matlab平臺下利用文獻［9］中的實驗數據建立支持向量機模型，計算基準狀況下壓氣機流量和效率性能參數。

首先建立壓氣機折合流量模型。對數據進行篩選，得到8組數據用來構建樣本集，其中壓比和折合轉速為輸入樣本集，折合流量為輸出樣本集。設定精度ε＝10－4，利用交叉驗證的方法得到最優參數組合為C＝724.08，σ＝32。訓練SV M回歸擬合模型，將樣本中的8組數據中輸入變量回代到訓練所得SV M模型中，可輸出相應的折合流量值。模型計算值與實驗值比較如圖1所示，最大相對誤差0.711%，平均相對誤差0.401%，與文獻中最大相對誤差1.06%和平均相對誤差0.323%的結果相當。

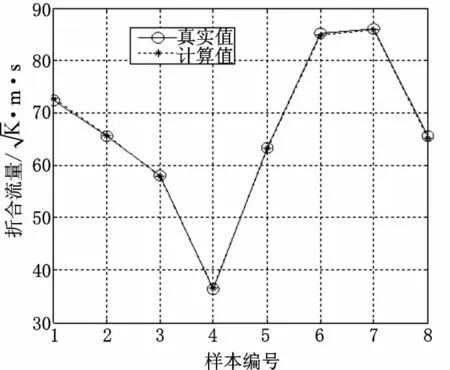
圖1 壓氣機折合流量計算結果

同理，按照前述方法對壓氣機效率進行建模，設定精度ε＝10－4，優化得到參數組合為C＝512，σ＝32，得到的壓氣機效率模型計算結果與實驗結果對比如圖2所示，最大相對誤差0.221%，平均相對誤差0.061%，低于文獻中最大相對誤差1.17%和平均相對誤差0.412%的精度。

從計算結果可以看出，此方法精度較高，利用該模型能很好地對燃氣輪機基準參數進行計算。

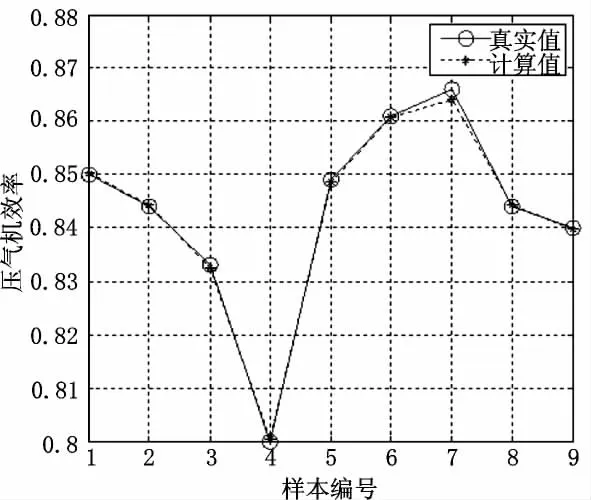
圖2 壓氣機效率計算結果

4 結語

針對燃氣輪機故障診斷中基準參數的計算問題，本文提出了利用支持向量機理論建立無故障狀態下基準參數計算模型的方法。結合故障診斷中通過可測參數獲得性能參數的研究思路，提出了建立基于支持向量機的基準參數一般計算模型的步驟，通過Matlab實現了模型的軟件計算，表明該方法可實現動態計算。利用支持向量機處理小樣本時學習能力強的特點，該支持向量機模型能利用有限的實驗數據進行建模，有利于減少實驗成本。在利用已有文獻實驗數據的仿真模擬中，該支持向量機模型的計算誤差均在1%以內，這表明模型具有很高的計算精度，能有效地計算燃氣輪機基準性能參數，對進一步研究燃氣輪機性能、進行故障診斷有著重要的價值和意義。

［1］楊欣毅，劉海峰，董可海.依據試驗數據求取航空發動機部件特性的新方法［J］.航空計算技術，2009（3）：48～55

［2］黃曉光，王永泓，翁史烈.燃氣輪機混合智能故障診斷專家系統［J］.船舶工程，2000（6）：37～39

［3］于美玲，劉永文.基于非線性模型的燃氣輪機熱參數故障診斷及仿真［J］.熱能能動力工程，2011（6）：651～654

［4］楊欣毅，劉劍鋒，張強，等.粒子群優化算法求解航空發動機模型的應用［J］.航空計算技術，2007（6）：39～44

［5］呂澤華，黃志明.三軸燃氣輪機變工況小偏差范圍內的解析解［J］.燃氣輪機技術，1995（2）：31～38

［6］徐玉兵.支持向量機在道路交通事故預測中的應用［J］.交通標準化，2010（1）：160～162

［7］Keerthi S，Lin C J.Asy mptotic behaviors of support vector machines with Gaussian ker nel［J］.Neural Computation，2003（7）：1 667～1 689

［8］王春林，周昊，李國能，等.基于支持向量機與遺傳算法的灰熔點預測［J］.2007（8）：11～15

［9］蔣磊，楊朔.基于Matlab的燃氣輪機熱參數故障診斷的標準數學模型建立［J］.科學技術與工程，2009（5）：1 254～1 257