超額吉布斯自由能-狀態方程模型的研究進展

蘭雪，夏力，項曙光

（青島科技大學煉油化工高新技術研究所，山東 青島 266042）

相平衡的計算有兩種方法，即狀態方程法和活度系數法。狀態方程法可以適用于壓力范圍較大的相平衡計算。針對混合物的相平衡進行計算中，必須使用相應的混合規則。對于強極性體系和強不對稱體系，狀態方程法使用傳統的混合規則會產生較大的誤差。活度系數法通常對低壓下的簡單和復雜化合物都有較好的應用，而且可以預測相平衡。但是由于交互作用參數的缺少，活度系數法不適用于高壓的情況。超額吉布斯自由能-狀態方程（GE-EoS）模型使用活度系數 GE模型計算得到混合規則，把狀態方程法和活度系數法結合起來，擴大了狀態方程的使用范圍。

1 GE-EoS模型的主體思想

GE-EoS模型的主體思想是：狀態方程計算出的超額吉布斯自由能等于活度系數模型計算出的超額吉布斯自由能，如式（1）所示。

以SRK方程為例，由狀態方程導出的超額吉布斯自由能如式（2）所示。

以式（3）計算得到b，將b帶入式（2），可以得到a關于GE的表達式，如式（4）。

式（4）中的GE以活度系數模型計算，這樣就將狀態方程和活度系數模型結合了起來。式（4）和式（2）即為得到的GE-EoS模型。

2 GE-EoS模型

自從HV混合規則提出后，GE-EoS模型發展迅速。目前已經有很多優秀的 GE-EoS模型應用于工業中的汽液相平衡計算和化工過程模擬軟件[1]。

為了得到簡單的GE混合規則，GE-EoS模型的參考壓力大多選擇無窮壓力或者是零壓力。

2.1 以無窮壓力為參考態的GE-EoS模型

以無窮壓力為參考態的 GE-EoS模型，最著名的是HV混合規則和WS混合規則。

2.1.1 HV混合規則

Huron和Vidal[2]提出了HV混合規則。HV混合規則作了兩點假設。

（2）在無窮壓力下，超額體積為零。

這一點假設就限定了 b必須使用線性混合規則，即式（3）。

根據以上兩點假設和式（1），可以得到HV混合規則的一般形式如式（5）。

式（5）中的C為與狀態方程有關的參數，EPG→∞為無窮壓力下的超額吉布斯自由能。

HV混合規則是第一個提出的GE-EoS模型，它與傳統的范德華混合規則相比，大大地擴大了狀態方程的使用范圍。Vidal等[2-3]曾使用HV混合規則結合SRK狀態方程和NRTL模型對丙酮/水、丙酮/環己烷、甲醇/CO2、乙烷/丙酮、丙烷/乙醇和一些其他的復雜混合物體系進行汽液相平衡關聯，得到了非常好的結果。

已知GE可以寫成如式（6）的形式。

由 HV混合規則的第一個假設可以得到 SE為零，HV的第二個假設是 VE為零。式（6）變成把 UNIFAC等活度系數模型分為組合項和剩余項，所以在無窮壓力下 GE本質上反映的是超額吉布斯自由能剩余項的貢獻。

Lermite等[3]使用 SRK/HV和 PR/HV結合UNIFAC的剩余項，對170對二元體系，其中包括含甲烷或乙烷的烴類混合物體系、含復雜石蠟烴體系、含芳香烴體系、含CO2體系，進行了泡點壓力和氣相組成進行了計算，絕大部分偏差都在 5%以內。

Feroiu等[4]提出了HVID模型。使用SRK方程和HV混合規則結合無限稀釋的UNIQUAC模型的剩余項，在較大的溫度范圍和壓力范圍內對異丙醇/水、甲醇/水、乙醇/水、丙酮/水、甲醇/苯、丙酮/甲醇六對二元體系的相平衡進行預測，得到了令人滿意的結果。壓力偏差和氣相組成偏差基本都在5%以內。Feroiu等[5]改進了HVID模型，用UNIFAC’93代替 UNIQUAC模型的剩余項，得到 HVIDUNIFAC’93模型，并對溫度范圍和壓力范圍都較大的4種情況進行了汽液平衡預測，都得到了很好的結果：①在低壓和高壓、低溫和高溫下的對稱極性體系；②含烷醇和烴類的體系；③含丙酮和烴類的體系；④烴類混合物。 HVID-UNIFAC’93混合規則還能應用于三元體系，得到令人滿意的結果。

HV混合規則主要有以下缺點：①要求超額體積為零，就決定b只能使用線性混合規則；②不符合第二維里系數的邊界條件；③活度系數模型都是由低壓下的數據回歸得到，所以HV模型不能直接使用現有的活度系數模型參數表。

2.1.2 WS混合規則

Wong和Sandler[6]提出了WS混合規則。該混合規則沿用了HV混合規則的無窮壓力參考態和第一個假設，所以混合規則中的a的形式依然采用HV的形式。

但是WS混合規則比HV混合規則在兩個方面有了改進。首先是考慮了AE對壓力的依賴要比GE小得多，有式（7）所示的近似關系。所以采用 AE代替GE，如式（7），這樣使得活度系數模型現有的參數表可用。

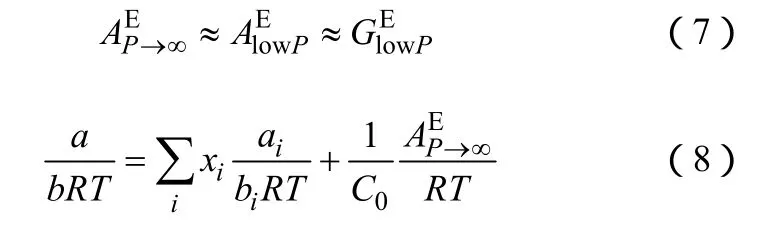
其次，b引入第二維里系數的形式，如式（9），這樣就符合了第二維里系數的邊界條件，使得 WS混合規則比HV混合規則更有理論基礎。

對WS混合規則的改進主要存在于3個方面。

（1）Bij計算方法的改變 Orbey和 Sandler[7]提出ijB的新的計算形式，如式（10）。

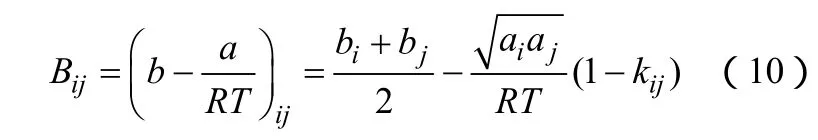
這種新的WS混合規則可以在一定的條件下轉化為范德華混合規則，但是并不會降低它的汽液平衡預測和關聯的能力，而且可以使用范德華混合規則長期以來積累的二元相互作用參數數據。此模型可以精確地預測復雜的二元和多元體系相平衡。

（2）kij計算方法的改進 Wong和Sandler使用在某個確定溫度、中間濃度的條件下得到的汽液平衡實驗數據，根據 GE模型回歸得到 kij。Huang和Sandler[8]用等摩爾組成時的GE模型的值求取kij。Orbey和 Sandler[7，9]使用無限稀釋活度系數下的UNIFAC模型求取 kij，這樣有更全面的預測性。Eubank等[10]用第二維里系數求取kij。

（3）WS混合規則形式的改進 Ali Haghtalab和 Reza Espanani[11]將WS混合規則結合PRSV狀態方程和修正的NRTL-NRF模型結合，在不同溫度下，將WS混合規則的應用拓展到不同分子量的聚合物溶液的汽液平衡預測并且得到與實驗數據相符合的結果。韓曉紅等[12]將WS混合規則中的kij簡化為只與組分和活度系數模型有關的函數。簡化的WS混合規則在較寬的溫度和壓力范圍內，與原始WS混合規則相比，精度基本相當。韓曉紅等[13]考慮了 WS混合規則忽略的分子體積大小差異的影響，提出了一個改進的WS混合規則。該混合規則對16組極性-極性、非極性-極性和非極性-非極性體系的汽液平衡進行關聯，比原始的WS混合規則精度有了一定的提高。吳選軍等[14]以常壓為參考態，提出了改進的 WS（MWS）混合規則，使用 SRK方程與MWS混合規則預測10個極性二元體系汽液平衡，結果略優于WS混合規則。Ye等[15]使用PR方程結合WS混合規則和PSRK中使用的UNIFAC模型（PRWS–UNIFAC–PSRK）、PR方程結合WS混合規則和UNIFAC-LBY模型（PRWS–UNIFAC–Lby），分別對H2O + MeOH + DME + CO2四元體系及其子體系的相平衡進行了預測。二元體系的參數能成功的拓展到三元和四元體系的汽液平衡和汽液液平衡，只是對于H2O + MeOH + DME的液液平衡結果不理想。

2.2 以零壓力為參考態的GE-EoS模型

Mollerup[16]和 Heidemann、Kokal[17]等最先提出以零壓力為參考態建立 GE-EoS模型的思想。但是在最初提出的模型中能量參數a隱含于V，所以要以迭代的方法得到a的值。直到1990年Michelsen等[18-20]改進了a的函數，提出了MHV1和MHV2混合規則，以零壓力為參考態的 GE-EoS模型才開始廣泛地應用于相平衡的計算中。MHV1和MHV2混合規則依然沿用了HV混合規則中對b使用的線性加和的方式。但是與 HV不同的是，MHV1和MHV2并不限制b必須采用線性加和的求取方式，也可以選擇滿足第二維里系數的混合規則。MHV1的一般形式如式（11）。

式（11）中，q0是與狀態方程有關的參數。對于SRK方程，q0=?0.593。

MHV2的一般形式如式（12）。

q的值可以通過q-a方程擬合得到，這樣其值依賴于所選擬合數據的適用范圍。q的值也可以通過堆積率得到[21]。

Holderbaum和Gmehling[22]使用SRK方程結合UNIFAC和MHV1混合規則，但是令q0=?0.64663，得到PSRK模型。

Li等[23]改進了PSRK中結合的UNIFAC模型的一些基團參數，改進后的PSRK對非對稱體系的相平衡預測結果表現良好。

零壓力為參考態的 GE-EoS模型無需重新擬合活度系數模型參數，在較寬的溫度和壓力范圍內，對極性化合物的相平衡有較好的預測結果。但是他們的預測結果和選擇的活度系數模型緊密相關。

汪萍[24]分別使用PSRK、MHV2和WS混合規則計算了相同的極性物系、高壓復雜體系和多元系的汽液平衡，并且對其結果作了詳細的比較。結果證明，PSRK混合規則在上述所有體系中結果均能給出較小偏差，是較好的混合規則。MHV2和WS對比于PSRK混合規則均顯示出了計算的局限性。MHV2和WS混合規則計算高壓體系的相平衡，結果都有較大偏差。WS混合規則不適合含有惰性氣體的復雜體系。

2.3 其他類型的GE-EoS模型

上述的以無窮壓力和以零壓力為參考態的GE-EoS模型有一個共同的缺陷，那就是都對于非對稱體系的相平衡計算和預測不能得到讓人滿意的結果。Boukouvalas等[25]提出了LCVM混合規則，形式如式（13）。LCVM是將無窮壓力下和零壓力下的GE-EoS模型線性組合得到的，不滿足式（1），所以它的得來基本沒有理論基礎，但是它在預測非對稱體系相平衡方面表現得極好。

式（13）中，AV、AM和λ為LCVM混合規則的模型參數。

Boukouvalas等分別使用 MHV2、PSRK和LCVM 混合規則計算了乙烷+n-正構烷烴、二氧化碳+n-正構烷烴和甲烷+n-正構烷烴等體系的相平衡。結果表明，隨著正構烷烴鏈長的增加，體系內物質的體積差別變大，MHV2和PSRK混合規則對相平衡的計算結果偏差快速變大。計算到n-C24時，MHV2和PSRK混合規則的偏差已經達到30%，而LCVM的偏差均在10%以內。LCVM在計算非對稱性體系時展現出了非常好的結果。

LCVM 對非對稱體系的相平衡有較好的結果并不是偶然的，其根本原因在于LCVM消除了狀態方程組合項和活度系數模型組合項的差異[26]。

韓曉紅等[27]借鑒LCVM混合規則的提出思路，將HVOS混合規則和MHV1線性組合，應用到多參數方程中。

Coniglio等[28]提出GCVM混合規則，即普遍化的LCVM型混合規則，如式（14）。

類似于LCVM的還有Orbey和Sandler[29]提出的CHV混合規則，如式（15）。

CHV混合規則使用了一個參數δ來減小對數項的貢獻。CHV混合規則與LCVM有兩點不同：①CHV混合規則有明確的參考壓力，即無窮壓力；②不像LCVM混合規則，參數λ影響超額自由能項和對數項，CHV混合規則中，參數δ只影響F-H對數項。

Jens Ahlers和 Gmehling[30]提出一個類似于PSRK的新的 GE-EoS模型。此模型基于 VTPR（volume translated Peng–Robinson）狀態方程，結合UNIFAC的剩余項，對b采用非線性混合規則，對非對稱體系的預測有很好的改進。其結果比Li-PSRK模型好，甚至可以和LCVM混合規則相比較。此外，對二氧化碳+乙烷體系，超額焓和超額體積的預測有很好的結果。

Tassios等[31]提出了一個普遍化的混合規則（UMR），其中 a的表達式中 GE使用原始的UNIFAC方程里組合項中的Staverman-Guggenheim項和剩余項。b使用密度依賴二次型的形式。此模型可以直接使用原始的UNIFAC的基團交互作用參數，在較大溫度和壓力范圍內，對非對稱體系的相平衡預測都能得到很好的結果。

3 結 論

GE-EoS模型通過GE將狀態方程和活度系數模型聯系起來，為相平衡的計算提供了新途徑。從最初的HV混合規則到適用于強不對稱體系的LCVM型混合規則，GE-EoS模型在適用范圍和相平衡預測精度上都有了很大的提高。

根據 GE-EoS模型的提出原理和發展歷程可以知道，對 GE-EoS模型的改進可以著手于以下幾個方面。

（1）改進狀態方程。使用能更精確描述流體P-V-T關系的狀態方程，例如改進的立方型狀態方程、多參數狀態方程或者 SAFT型方程，會改進GE-EoS模型計算和預測相平衡的精度。

（2）改進活度系數模型的形式。例如文獻[4]中提到的GE-EoS模型，只利用UNIFAC的剩余項。

（3）擴充活度系數模型的參數表。例如UNIFAC的參數一直在進行修補和增訂，這必將擴大相應的GE-EoS模型的適用范圍。

經過多年的發展，適用于對稱體系 GE-EoS模型發展得已經較為成熟。發展針對于非對稱體系的、消除組合項差異的GE-EoS模型將是新的主流。

符 號 說 明

AE—— 超額亥姆霍茲自由能，J/mol

AM，AV—— 分別為LCVM混合規則的模型參數，量綱為1

a—— 狀態方程混合物的能量參數，kPa·m6·K0.5/mol2

ai，aj—— 分別為狀態方程純物質的能量參數，kPa·m6· K0.5/mol2

B —— 第二維里系數，m3/mol

Bij—— 二元交叉維里系數，m3/mol

b—— 狀態方程混合物的協體積參數，m3/mol

bi，bj—— 分別為狀態方程純物質的協體積參數，m3/mol

C—— HV混合規則的模型參數，量綱為1

C0—— WS混合規則的模型參數，量綱為1

C1，C2—— 分別為GCVM混合規則的模型參數，量綱為1

C*—— CHV混合規則的模型參數，量綱為1

E—— 超額性質

FH—— Flory?Huggins模型

GE——超額吉布斯自由能，J/mol

i，j—— 組分

kij——二元相互作用參數，量綱為1

lowP——低壓，kPa

M——活度系數模型

P——壓力，kPa

q0——MHV1和PSRK混合規則的模型參數，量綱為1

q1，q2——分別為MHV2混合規則的模型參數，量綱為1

R——氣體常數，8.314J/(mol·K)

SE—— 超額熵，J/(mol·K)

T——溫度，K

UE——超額內能，J/mol

V——混合物的摩爾體積，m3/mol

Vi——純物質的摩爾體積，m3/mol

VE——超額體積，m3/mol

x——液相摩爾分數，量綱為1

δ——CHV混合規則的模型參數，量綱為1

λ——LCVM混合規則的模型參數，量綱為1

φ——混合物的逸度系數，量綱為1

φi——純物質的逸度系數，量綱為1

∞——無窮壓力，kPa

0——零壓力，kPa

[1]Chen C C，Mathias P M. Applied thermodynamics for process modeling[J]. AIChE Journal，2002，48（2）：194-200.

[2]Huron M J，Vidal. New mixing rules in simple equations of state for representing vapour-liquid equilibria of strongly non-ideal mixtures[J].Fluid Phase Equilibria，1979，3（4）：255-271.

[3]Lermite C，Vidal J. High pressure polar compounds phase equilibria calculation：Mixing rules and excess properties[J]. Fluid Phase Equilibria，1988，42：1-19.

[4]Feroiu V，Gean? D. Prediction of vapor-liquid equilibria at high pressures using activity coefficients at infinite dilution[J]. Fluid Phase Equilibria，1996，120（1）：1-10.

[5]Gean? D，Feroiu V. Prediction of vapor-liquid equilibria at low and high pressures from UNIFAC activity coefficients at infinite dilution[J]. Industrial & Engineering Chemistry Research，1998，37（3）：1173-1180.

[6]Wong D S H，Sandler S I. A theoretically correct mixing rule for cubic equations of state[J]. AIChE Journal，1992，38（5）：671-680.

[7]Orbey H，Sandler S I. Reformulation of Wong-Sandler mixing rule for cubic equations of state[J]. AIChE Journal，1995，41（3）：683-690.

[8]Huang H，Sandler S I，Orbey H. Vapor-liquid equilibria of some hydrogen + hydrocarbon systems with the Wong-Sandler mixing rule[J]. Fluid Phase Equilibria，1994，96：143-153.

[9]Orbey H，Sandler S I. Modeling Vapor-Liquid Equilibria：Cubic equations of state and their mixing rules[M]. Oxford：Cambridge University Press，1998.

[10]Eubank P T，Shyu G S，Hanif N S M. New procedures for application of the Wong-Sandler mixing rules to the prediction of vapor-liquid equilibria[J]. Industrial & Engineering Chemistry Research，1995，34（1）：314-323.

[11]Haghtalab A，Espanani R. A new model and extension of Wong–Sandler mixing rule for prediction of （vapour + liquid）equilibrium of polymer solutions using EOS/GE[J]. The Journal of Chemical Thermodynamics，2004，36（10）：901-910.

[12]韓曉紅，陳光明，王勤，等. 簡化的 WS 混合規則在汽液相平衡中的應用[J]. 工程熱物理學報，2005，26（5）：721-724.

[13]韓曉紅，陳光明，王勤. 基于無窮壓力為參考態的超額自由能混合規則[J]. 工程熱物理學報，2006，27（6）：905-907.

[14]吳選軍，張光旭，劉相鵬. SRK 方程結合超額 Gibbs 自由能規則預測汽液平衡[J]. 化學工程，2010（1）：63-66.

[15]Ye K，Freund H，Sundmacher K. Modelling (vapour + liquid) and(vapour + liquid + liquid) equilibria of {water (H2O) + methanol(MeOH) + dimethyl ether (DME) + carbon dioxide (CO2)} quaternary system using the Peng–Robinson EoS with Wong–Sandler mixing rule[J]. The Journal of Chemical Thermodynamics，2011，43（12）：2002-2014.

[16]Mollerup J. A note on the derivation of mixing rules from excess Gibbs energy models[J]. Fluid Phase Equilibria，1986，25（3）：323-327.

[17]Heidemann R A，Kokal S L. Combined excess free energy models and equations of state[J]. Fluid Phase Equilibria，1990，56：17-37.

[18]Michelsen M L. A method for incorporating excess Gibbs energy models in equations of state[J]. Fluid Phase Equilibria，1990，60（1）：47-58.

[19]Michelsen M L. A modified Huron-Vidal mixing rule for cubic equations of state[J]. Fluid Phase Equilibria，1990，60（1）：213-219.

[20]Dahl S，Michelsen M L. High-pressure vapor‐liquid equilibrium with a UNIFAC‐based equation of state[J]. AIChE Journal，1990，36（12）：1829-1836.

[21]Kontogeorgis G M，Coutsikos P. Thirty years with EoS/GEmodels：What have we learned？[J]. Industrial & Engineering Chemistry Research，2012，51（11）：4119-4142.

[22]Holderbaum T，Gmehling J. PSRK：A group contribution equation of state based on UNIFAC[J]. Fluid Phase Equilibria，1991，70（2）：251-265.

[23]Li J，Fischer K，Gmehling J. Prediction of vapor-liquid equilibria for asymmetric systems at low and high pressures with the PSRK model[J]. Fluid Phase Equilibria，1998，143（1-2）：71-82.

[24]汪萍. 立方型狀態方程性能的評價研究[D]. 青島：青島科技大學，2004.

[25]Boukouvalas C，Spiliotis N，Coutsikos P，et al. Prediction of vapor-liquid equilibrium with the LCVM model：A linear combination of the Vidal and Michelsen mixing rules coupled with the original UNIF[J]. Fluid Phase Equilibria，1994，92：75-106.

[26]陳明君，傅楊武. EOS/GE模型預測非對稱體系相平衡的進展[J].中國西部科技，2009，24（8）：5-7.

[27]韓曉紅，陳光明，王勤. LCVM 型混合規則擴展用于多參數狀態方程以關聯混合物汽液相平衡[J]. 高校化學工程學報，2006（2）：159-163.

[28]Coniglio L，Knudsen K，Gani R. Prediction of supercritical fluid-liquid equilibria for carbon dioxide and fish oil related compounds through the equation of state—excess function (EOS-GE)approach[J]. Fluid Phase Equilibria，1996，116（1）：510-517.

[29]Orbey H，Sandler S I. Analysis of excess free energy based equations of state models[J]. AIChE Journal，1996，42（8）：2327-2334.

[30]Ahlers J，Gmehling J. Development of a universal group contribution equation of state. 2. Prediction of vapor-liquid equilibria for asymmetric systems[J]. Industrial & Engineering Chemistry Research，2002，41（14）：3489-3498.

[31]Voutsas E，Magoulas K，Tassios D. Universal mixing rule for cubic equations of state applicable to symmetric and asymmetric systems：Results with the Peng-Robinson equation of state[J]. Industrial &Engineering Chemistry Research，2004，43（19）：6238-6246.