R函數(shù)實(shí)現(xiàn)正態(tài)總體均值、方差的區(qū)間估計(jì)及假設(shè)檢驗(yàn)的設(shè)計(jì)
張應(yīng)應(yīng),魏 毅
(重慶大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,重慶 401331)
0 引言
正態(tài)總體均值、方差的區(qū)間估計(jì)與假設(shè)檢驗(yàn)是數(shù)理統(tǒng)計(jì)中的經(jīng)典內(nèi)容。數(shù)理統(tǒng)計(jì)的教材[1~6]一般都會(huì)講到。針對(duì)摘要中提到的R軟件[7]內(nèi)置程序t.test()、var.test()函數(shù)的缺陷,參考文獻(xiàn)[1]中為實(shí)現(xiàn)單個(gè)、兩個(gè)正態(tài)總體均值、方差的區(qū)間估計(jì)、假設(shè)檢驗(yàn)時(shí)自編了12個(gè)函數(shù)interval_estimate1()、 interval_estimate2()、 interval_estimate4()、 interval_estimate5()、interval_var1()、interval_var2()、interval_var3()、interval_var4()、mean.test1()、mean.test2()、var.test1()、var.test2(),這些函數(shù)可以實(shí)現(xiàn)R軟件的內(nèi)置函數(shù)t.test()、var.test()的全部功能,并能有效彌補(bǔ)t.test()和var.test()的缺陷。但是要記住并靈活掌握這么多函數(shù)是一件非常麻煩的事情,并且我們也常常同時(shí)需要區(qū)間估計(jì)和假設(shè)檢驗(yàn)的結(jié)果。本文在文獻(xiàn)[1]的啟發(fā)下創(chuàng)造了一個(gè)R函數(shù)Interval-Estimate_TestOfHypothesis(),它可以實(shí)現(xiàn) t.test()和 var.test()的所有功能及它們不能完成的上述功能,只用一個(gè)R函數(shù)便能實(shí)現(xiàn)單個(gè)、兩個(gè)正態(tài)總體均值、方差的所有區(qū)間估計(jì)及假設(shè)檢驗(yàn)。
1 程序設(shè)計(jì)
1.1 P值計(jì)算
在軟件計(jì)算中,通常計(jì)算隨機(jī)變量X大于或小于某個(gè)指定值的概率,稱為P值。
以正態(tài)分布為例,在給定z值后,計(jì)算原理[1]如下:
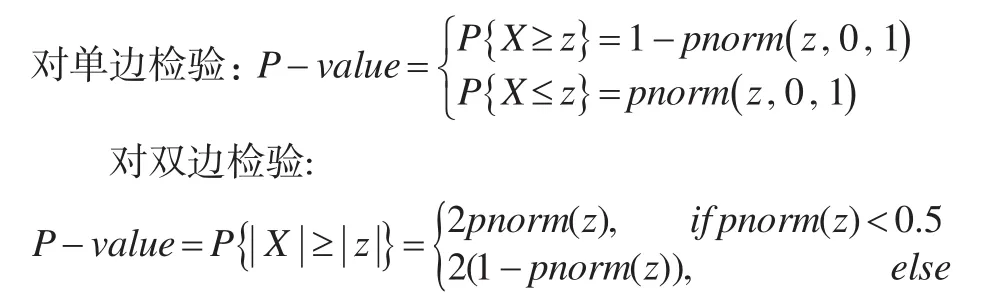
圖1 正態(tài)總體雙邊檢驗(yàn)(H1: μ≠μ0)

圖2 正態(tài)總體單邊檢驗(yàn)(H1: μ>μ0)
考慮到假設(shè)檢驗(yàn)中多處需要計(jì)算P值,編寫R函數(shù)p_value.R來實(shí)現(xiàn)不同分布P值的計(jì)算。相應(yīng)的,當(dāng)給定概率值α?xí)r,可計(jì)算出對(duì)應(yīng)的上分位數(shù)q值,編寫R函數(shù)q_value.R來實(shí)現(xiàn)不同分布分位數(shù)的計(jì)算。
1.2 值的區(qū)間估計(jì)和假設(shè)檢驗(yàn)
1.2.1 單個(gè)正態(tài)總體
正態(tài)總體 X~N(μ,σ2),X1,X2,…,Xn為來自總體 X的一個(gè)樣本,1-α為置信度,為樣本均值,S2為樣本方差。在作總體X均值的區(qū)間估計(jì)時(shí),需分別討論方差σ2已知和未知兩種情形;作假設(shè)檢驗(yàn)時(shí),在單邊、雙邊檢驗(yàn)情況同樣需要區(qū)分方差σ2已知和未知[1]。程序設(shè)計(jì)見下圖3。
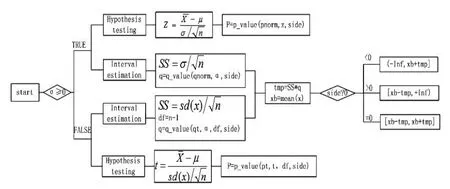
圖3
編寫R函數(shù)命名為single_mean.R
1.2.2 兩個(gè)正態(tài)總體
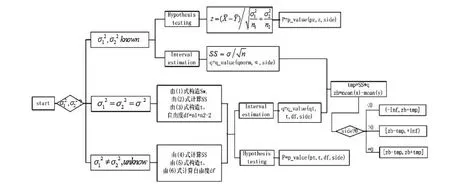
圖4
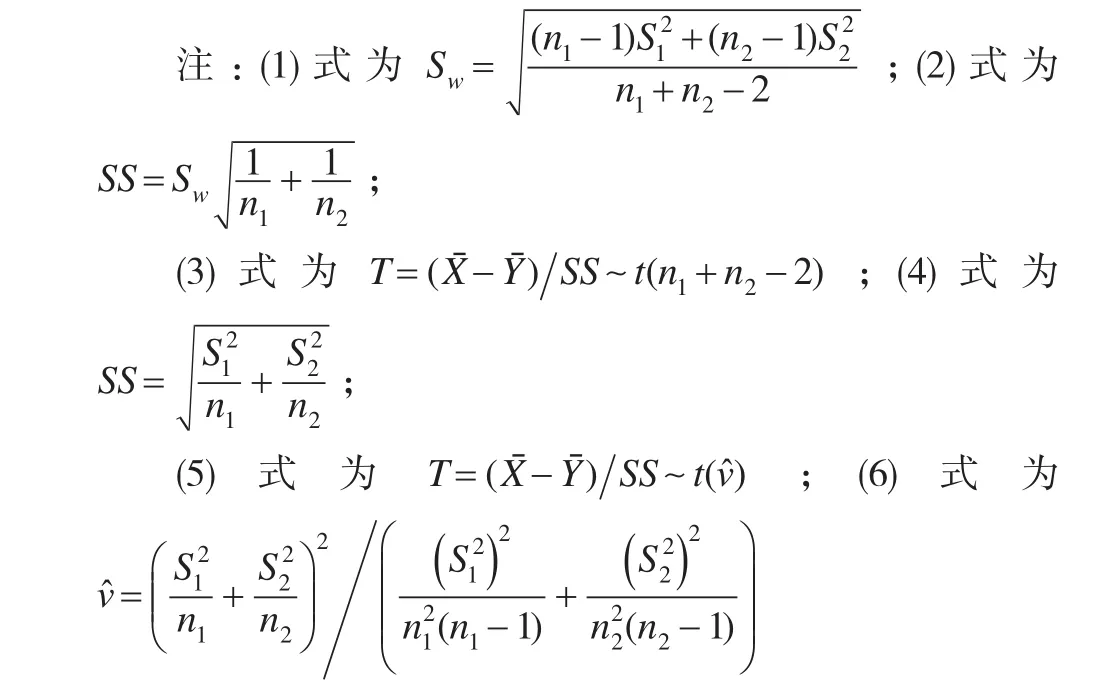
編寫R函數(shù)命名為double_mean.R
1.3 方差的區(qū)間估計(jì)和假設(shè)檢驗(yàn)
1.3.1 單個(gè)正態(tài)總體
作方差的區(qū)間估計(jì)時(shí),分總體X的均值μ已知和未知兩種情形討論,作假設(shè)檢驗(yàn)時(shí),又須在μ已知和未知的情形下分單邊、雙邊檢驗(yàn)。程序設(shè)計(jì)類似于單個(gè)正態(tài)總體均值的區(qū)間估計(jì)和假設(shè)檢驗(yàn),故省略。編寫R函數(shù)命名為single_var.R
1.3.2 兩個(gè)正態(tài)總體
2 R函數(shù)IntervalEstimate_TestOfHypothesis()
在以上程序基礎(chǔ)上,還需編寫主函數(shù)來調(diào)用子程序以實(shí)現(xiàn)不同的功能,主函數(shù)使用格式如下:
IntervalEstimate_TestOfHypothesis(x,y=NULL,test=c(“mean”,“variance”),mu=c(Inf,Inf),sigma=c(-1,-1),var.equal=FALSE,ratio=1,side=c(“two.sided”,“l(fā)ess”,“greater”),alpha=0.05)
其中x,y是由樣本數(shù)據(jù)構(gòu)成的向量;
y默認(rèn)值為NULL,即默認(rèn)為對(duì)單總體進(jìn)行操作;
test為檢驗(yàn)的類型,默認(rèn)值為“mean”,代表作均值的區(qū)間估計(jì)和假設(shè)檢驗(yàn),test=“variance”或”var”代表作方差的區(qū)間估計(jì)和假設(shè)檢驗(yàn);
mu為總體的均值向量,在方差的區(qū)間估計(jì)和假設(shè)檢驗(yàn)以及單總體均值的假設(shè)檢驗(yàn)中會(huì)用到,默認(rèn)值為Inf(即未知);
sigma為總體的標(biāo)準(zhǔn)差向量,默認(rèn)值均為-1(即未知),當(dāng)程序用于作單總體方差假設(shè)檢驗(yàn)時(shí),默認(rèn)為檢驗(yàn)σ2=1;
var.equal判斷兩總體方差是否相等,默認(rèn)為FALSE,此參數(shù)在兩總體均值檢驗(yàn)中用到;
ratio為兩總體方差比率,默認(rèn)為1,此參數(shù)在兩總體方差檢驗(yàn)中用到;
side判斷求置信區(qū)間和作假設(shè)檢驗(yàn)的類型,默認(rèn)值為”two.sided”,即作雙邊檢驗(yàn)并求雙側(cè)置信區(qū)間;side=”less”或“l(fā)”,表示求置信區(qū)間上限并作單邊檢驗(yàn)(H1: μ<μ0);side=”greater”或“g”,表示求置信區(qū)間下限并作單邊檢驗(yàn)(H1: μ>μ0);
alpha為一個(gè)取值為[0,1]的實(shí)數(shù),默認(rèn)為0.05,1-alpha為置信度。
由于本程序是對(duì)正態(tài)總體進(jìn)行操作,因此,在使用本函數(shù)前須先確認(rèn)樣本數(shù)據(jù)服從正態(tài)分布,為此,編寫R程序testNormal_plot.R來對(duì)樣本做正態(tài)性檢驗(yàn),其調(diào)用格式為:

表1 正態(tài)總體區(qū)間估計(jì)及假設(shè)檢驗(yàn)函數(shù)IntervalEstimate_TestOfHypothesis()的使用方法表
testNormal_plot(x,alpha)
其中x為待測(cè)樣本向量,alpha意義同上。
表1中,side=”two.sided”(程序默認(rèn)值,可不必輸入)表示求雙側(cè)置信區(qū)間并作雙邊檢驗(yàn),alpha=0.05(默認(rèn)值,可不必輸入)表示顯著性水平為0.05,test=”var”(效果與test=”variance”相同)表示對(duì)輸入變量作方差的區(qū)間估計(jì)和假設(shè)檢驗(yàn),ratio=2(ratio=默認(rèn)值為1),代表作兩總體方差檢驗(yàn)的原假設(shè)為
接下來,將舉例來測(cè)試函數(shù)IntervalEstimate_TestOf-Hypothesis()(以下簡(jiǎn)稱待測(cè)函數(shù)),以驗(yàn)證其正確性。
testNormal_plot()用于測(cè)試數(shù)據(jù)x是否來自正態(tài)總體。
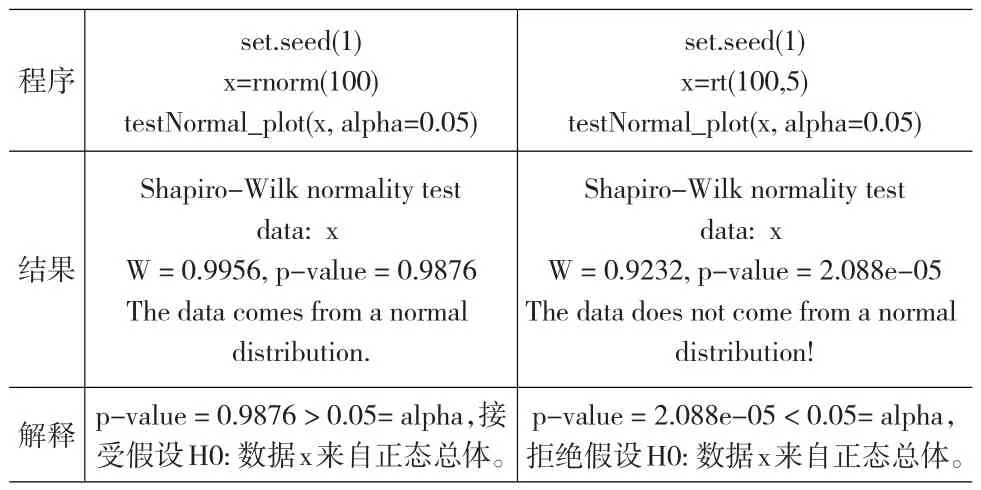
程序結(jié)果解釋set.seed(1)x=rnorm(100)testNormal_plot(x,alpha=0.05)Shapiro-Wilk normality test data:x W=0.9956,p-value=0.9876 The data comes from a normal distribution.p-value=0.9876 > 0.05=alpha,接受假設(shè)H0:數(shù)據(jù)x來自正態(tài)總體。set.seed(1)x=rt(100,5)testNormal_plot(x,alpha=0.05)Shapiro-Wilk normality test data:x W=0.9232,p-value=2.088e-05 The data does not come from a normal distribution!p-value=2.088e-05<0.05=alpha,拒絕假設(shè)H0:數(shù)據(jù)x來自正態(tài)總體。
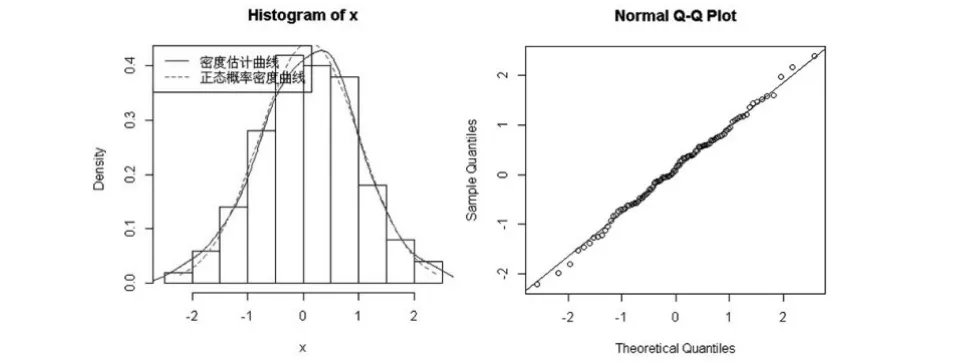
正態(tài)隨機(jī)數(shù)檢驗(yàn)圖像
產(chǎn)生樣本x,此x將用于例1~例4的測(cè)試

程序結(jié)果解釋set.seed(1)x=rnorm(10,mean=1,sd=0.2);x[1]0.8747092 1.0367287 0.8328743 1.3190562 1.0659016[6]0.8359063 1.0974858 1.1476649 1.1151563 0.9389223產(chǎn)生一個(gè)來自正態(tài)總體的均值為1,標(biāo)準(zhǔn)差為0.2的容量為10的樣本,為便于重復(fù)結(jié)果,我們使用set.seed(1)。
例1:單總,均值,sigma2(即 σ2,下同)已知

程序結(jié)果解釋testNormal_plot(x)Shapiro-Wilk normality test data:x W=0.9383,p-value=0.534 The data comes from a normal distribution.p-value=0.534>0.05=alpha,接受假設(shè)H0:數(shù)據(jù)x來自正態(tài)總體。
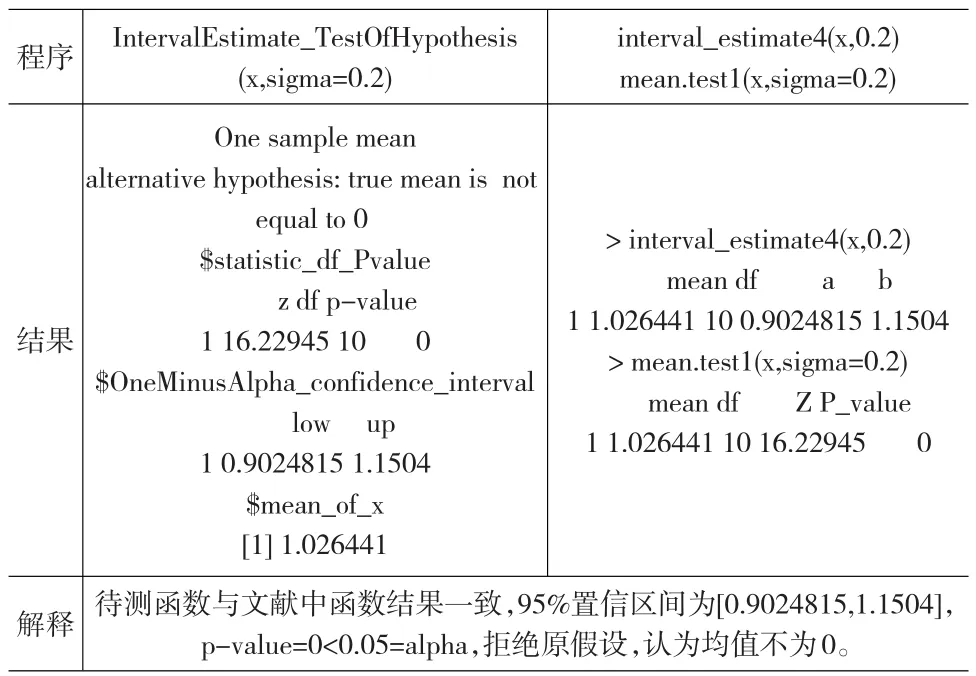
程序結(jié)果解釋IntervalEstimate_TestOfHypothesis(x,sigma=0.2)One sample mean alternative hypothesis:true mean is not equal to 0$statistic_df_Pvalue z df p-value 1 16.22945 10 0$OneMinusAlpha_confidence_interval low up 1 0.9024815 1.1504$mean_of_x[1]1.026441待測(cè)函數(shù)與文獻(xiàn)中函數(shù)結(jié)果一致,95%置信區(qū)間為[0.9024815,1.1504],p-value=0<0.05=alpha,拒絕原假設(shè),認(rèn)為均值不為0。interval_estimate4(x,0.2)mean.test1(x,sigma=0.2)>interval_estimate4(x,0.2)mean df a b 1 1.026441 10 0.9024815 1.1504>mean.test1(x,sigma=0.2)mean df Z P_value 1 1.026441 10 16.22945 0
例2:單總,均值,sigma2未知
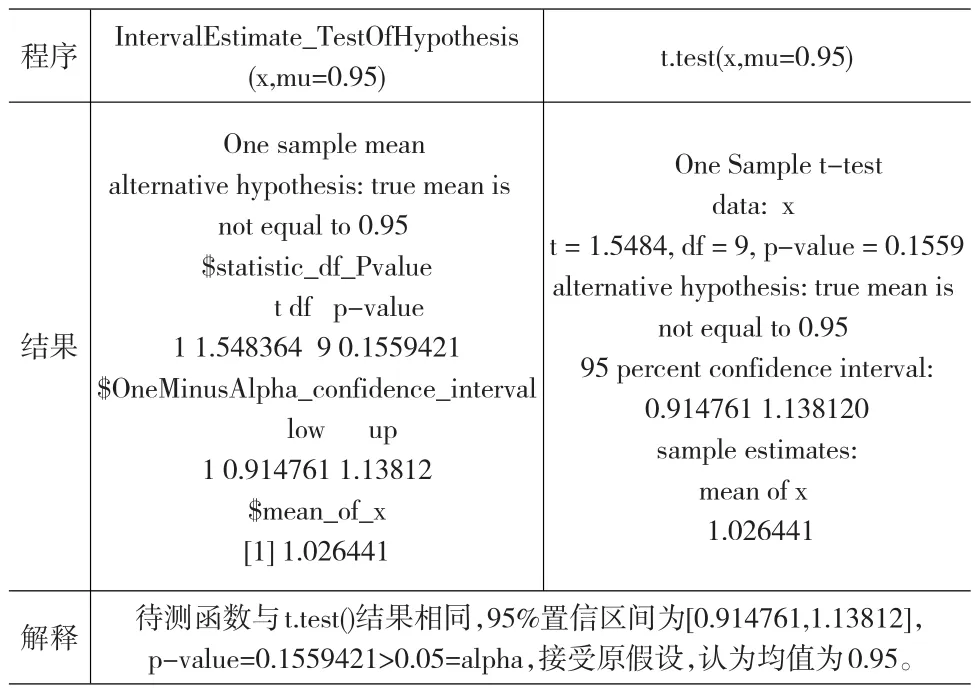
程序結(jié)果解釋IntervalEstimate_TestOfHypothesis(x,mu=0.95)One sample mean alternative hypothesis:true mean is not equal to 0.95$statistic_df_Pvalue t df p-value 1 1.548364 9 0.1559421$OneMinusAlpha_confidence_interval low up 1 0.914761 1.13812$mean_of_x[1]1.026441待測(cè)函數(shù)與t.test()結(jié)果相同,95%置信區(qū)間為[0.914761,1.13812],p-value=0.1559421>0.05=alpha,接受原假設(shè),認(rèn)為均值為0.95。t.test(x,mu=0.95)One Sample t-test data:x t=1.5484,df=9,p-value=0.1559 alternative hypothesis:true mean is not equal to 0.95 95 percent confidence interval:0.914761 1.138120 sample estimates:mean of x 1.026441
例3:單總,方差,mu已知,sigma不輸入時(shí),默認(rèn)檢測(cè)σ2=1
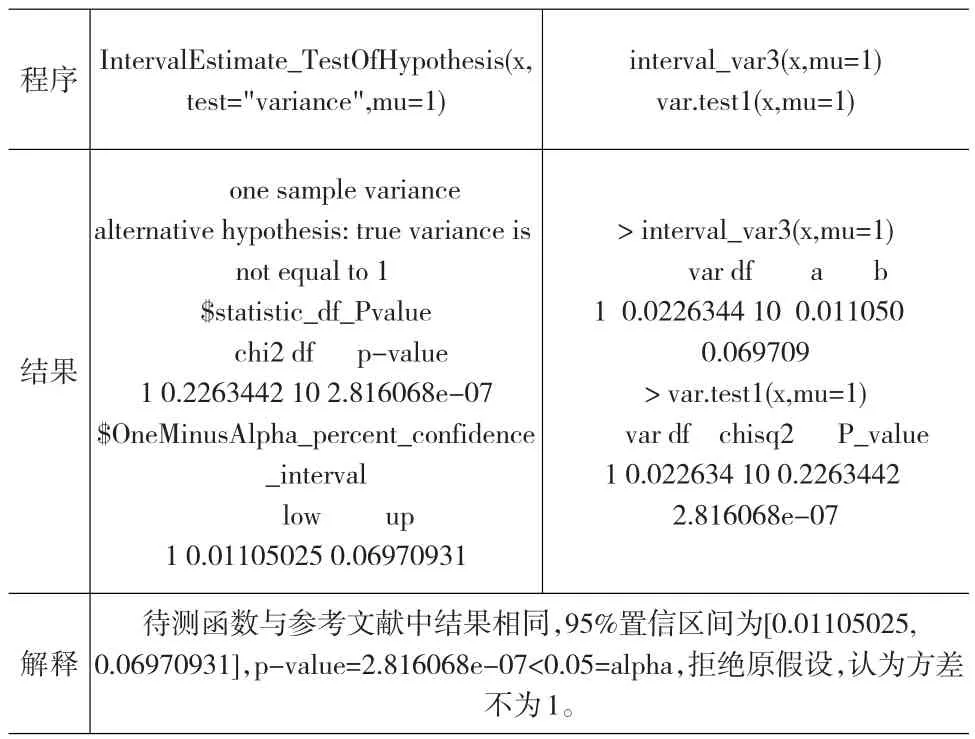
程序結(jié)果解釋IntervalEstimate_TestOfHypothesis(x,test="variance",mu=1)one sample variance alternative hypothesis:true variance is not equal to 1$statistic_df_Pvalue chi2 df p-value 1 0.2263442 10 2.816068e-07$OneMinusAlpha_percent_confidence_interval low up 1 0.01105025 0.06970931待測(cè)函數(shù)與參考文獻(xiàn)中結(jié)果相同,95%置信區(qū)間為[0.01105025,0.06970931],p-value=2.816068e-07<0.05=alpha,拒絕原假設(shè),認(rèn)為方差不為1。interval_var3(x,mu=1)var.test1(x,mu=1)>interval_var3(x,mu=1)var df a b 1 0.0226344 10 0.011050 0.069709>var.test1(x,mu=1)var df chisq2 P_value 1 0.022634 10 0.2263442 2.816068e-07
例4:單總,方差,mu未知

程序結(jié)果解釋IntervalEstimate_TestOfHypothesis(x,test="variance",sigma=0.18)one sample variance alternative hypothesis:true variance is not equal to 0.0324$statistic_df_Pvalue chi2 df p-value 1 6.77016 9 0.6779301$OneMinusAlpha_percent_confidence_interval low up 1 0.01153109 0.08123021待測(cè)函數(shù)與文獻(xiàn)中函數(shù)結(jié)果相同,95%置信區(qū)間為[0.01153109,0.08123021],p-value=0.6779301>0.05=alpha,接受原假設(shè),認(rèn)為標(biāo)準(zhǔn)差為0.18。interval_var3(x)var.test1(x,sigma2=0.18^2)>interval_var3(x)var df a b 1 0.024372 9 0.011531 0.08123021>var.test1(x,sigma2=0.18^2)var df chisq2 P_value 1 0.02437258 9 6.77016 0.6779301
產(chǎn)生正態(tài)樣本,此x,y1,y2將用于例5~例9的測(cè)試
set.seed(1);x=rnorm(10,mean=1,sd=0.2);x
set.seed(2);y1=rnorm(15,mean=2,sd=0.3);y1
set.seed(2);y2=rnorm(15,mean=2,sd=0.2);y2
testNormal_plot(y1)
testNormal_plot(y2)
以下的數(shù)據(jù)正態(tài)性檢驗(yàn)與之前相似,檢驗(yàn)結(jié)果不再列出。
例5:雙總,均值,方差已知
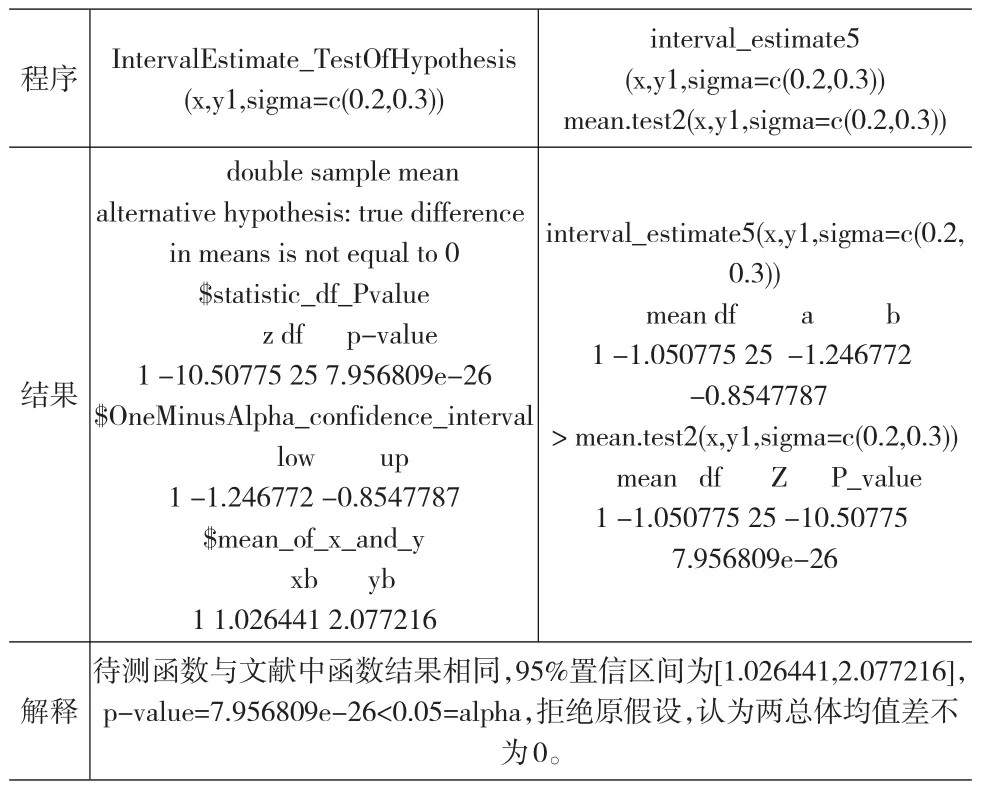
程序結(jié)果解釋IntervalEstimate_TestOfHypothesis(x,y1,sigma=c(0.2,0.3))double sample mean alternative hypothesis:true difference in means is not equal to 0$statistic_df_Pvalue z df p-value 1-10.50775 25 7.956809e-26$OneMinusAlpha_confidence_interval low up 1-1.246772-0.8547787$mean_of_x_and_y xb yb 1 1.026441 2.077216待測(cè)函數(shù)與文獻(xiàn)中函數(shù)結(jié)果相同,95%置信區(qū)間為[1.026441,2.077216],p-value=7.956809e-26<0.05=alpha,拒絕原假設(shè),認(rèn)為兩總體均值差不為0。interval_estimate5(x,y1,sigma=c(0.2,0.3))mean.test2(x,y1,sigma=c(0.2,0.3))interval_estimate5(x,y1,sigma=c(0.2,0.3))mean df a b 1-1.050775 25-1.246772-0.8547787>mean.test2(x,y1,sigma=c(0.2,0.3))mean df Z P_value 1-1.050775 25-10.50775 7.956809e-26
例6:雙總,均值,方差未知但相等

程序結(jié)果解釋IntervalEstimate_TestOfHypothesis(x,y2,var.equal=T)double sample mean alternative hypothesis:true difference in means is not equal to 0$statistic_df_Pvalue t df p-value 1-13.73411 23 1.429158e-12$OneMinusAlpha_confidence_interval low up 1-1.17943-0.8706436$mean_of_x_and_y xb yb 1 1.026441 2.051477待測(cè)函數(shù)與t.test()結(jié)果相同,95%置信區(qū)間為[-1.17943,-0.8706436],p-value=1.429158e-12<0.05=alpha,拒絕原假設(shè),認(rèn)為兩總體均值差不為0。t.test(x,y2,var.equal=T)Two Sample t-test data:x and y2 t=-13.7341,df=23,p-value=1.429e-12 alternative hypothesis:true difference in means is not equal to 0 95 percent confidence interval:-1.1794296-0.8706436 sample estimates:mean of x mean of y 1.026441 2.051477
例7:雙總,均值,方差未知且不等

程序結(jié)果解釋IntervalEstimate_TestOfHypothesis(x,y1,var.equal=F,side="less")double sample mean alternative hypothesis:true difference in means is less than 0$statistic_df_Pvalue t df p-value 1-11.51773 22.10023 4.112604e-11$OneMinusAlpha_confidence_interval low up 1-Inf-0.8941493$mean_of_x_and_y xb yb 1 1.026441 2.077216待測(cè)函數(shù)與t.test()結(jié)果相同,95%置信區(qū)間為[-Inf,-0.8941493],p-value=4.112604e-11<0.05=alpha,拒絕原假設(shè),認(rèn)為兩總體均值差小于0。t.test(x,y1,var.equal=F,al='less')Welch Two Sample t-test data:x and y1 t=-11.5177,df=22.1,p-value=4.113e-11 alternative hypothesis:true difference in means is less than 0 95 percent confidence interval:-Inf-0.8941493 sample estimates:mean of x mean of y 1.026441 2.077216
說明:例1~例9基本覆蓋了單個(gè)、兩個(gè)正態(tài)總體均值、方差的區(qū)間估計(jì)和假設(shè)檢驗(yàn)的所有情況,IntervalEstimate_TestOfHypothesis()運(yùn)行的結(jié)果與R內(nèi)置函數(shù)t.test(),var.test()所得的結(jié)果完全一致,對(duì)于t.test(),var.test()所不能解決的例子(包括例1,例3,例4,例5,例8),筆者使用參考文獻(xiàn)中的函數(shù)interval_estimate4(),interval_estimate5(),interval_var3(),interval_var4(),mean.test1(),mean.test2(),var.test1(),var.test2()進(jìn)行了檢測(cè),結(jié)果也完全吻合。
例8:雙總,方差,均值已知

程序結(jié)果解釋IntervalEstimate_TestOfHypothesis(x,y1,test="var",mu=c(1,2))double sample variance alternative hypothesis:true ratio of the variances is not equal to 1$statistic_df_Pvalue f df1 df2 p-value 1 0.2561489 10 15 0.03500855$OneMinusAlpha_percent_confidence_interval low up 1 0.0837034 0.9020726$ratio_of_variances[1]0.2561489待測(cè)函數(shù)與文獻(xiàn)中函數(shù)結(jié)果相同,95%置信區(qū)間為[0.0837034,0.9020726],p-value=0.03500855<0.05=alpha,拒絕原假設(shè),認(rèn)為方差比率不為1。interval_var4(x,y1,mu=c(1,2))var.test2(x,y1,mu=c(1,2))>interval_var4(x,y1,mu=c(1,2))rate df1 df2 a b 1 0.2561489 10 15 0.0837034 0.9020726>var.test2(x,y1,mu=c(1,2))Rate df1 df2 F P_value 1 0.2561489 10 15 0.2561489 0.03500855
例9:雙總,方差,均值未知

程序結(jié)果解釋IntervalEstimate_TestOfHypothesis(x,y1,test="var",ratio=2,side="g")double sample variance alternative hypothesis:true ratio of the variances is greater than 2$statistic_df_Pvalue f df1 df2 p-value 1 0.1380289 9 14 0.9973642$OneMinusAlpha_percent_confidence_interval low up 1 0.1043385 Inf$ratio_of_variances[1]0.2760579待測(cè)函數(shù)與var.test()結(jié)果相同,95%單側(cè)置信區(qū)間為[0.1043385,Inf],p-value=0.9973642>0.05=alpha,接受原假設(shè),認(rèn)為方差比率小于或等于2。var.test(x,y1,ratio=2,al="g")F test to compare two variances data:x and y1 F=0.138,num df=9,denom df=14,p-value=0.9974 alternative hypothesis:true ratio of variances is greater than 2 95 percent confidence interval:0.1043385 Inf sample estimates:ratio of variances 0.2760579
3 結(jié)論
本文通過簡(jiǎn)要的理論分析,編寫的函數(shù)IntervalEstimate_TestOfHypothesis()很好地解決了R軟件內(nèi)置函數(shù)t.test()、var.test()的缺陷,同時(shí)其參數(shù)設(shè)計(jì)也簡(jiǎn)單明了,將為需要作相關(guān)正態(tài)總體區(qū)間估計(jì)和假設(shè)檢驗(yàn)的使用者提供方便。
[1]薛毅,陳麗萍.統(tǒng)計(jì)建模與R軟件[M].北京:清華大學(xué)出版社,2007.
[2]陳希孺,倪國(guó)熙,陳長(zhǎng)順.數(shù)理統(tǒng)計(jì)學(xué)教程[M].安徽:中國(guó)科學(xué)技術(shù)大學(xué)出版社,2009.
[3]楊虎,劉瓊蓀,鐘波.數(shù)理統(tǒng)計(jì)[M].北京:高等教育出版社,2004.
[4]王學(xué)民.多元應(yīng)用分析[M].上海:上海財(cái)經(jīng)大學(xué)出版社,2009.
[5]David Freedman等著,魏宗舒等譯.統(tǒng)計(jì)學(xué)[M].北京:中國(guó)統(tǒng)計(jì)出版社,1997.
[6]鄭忠國(guó).高等統(tǒng)計(jì)學(xué)[M].北京:北京大學(xué)出版社,2012.
[7]R Core Team.R:A Language and Environment for Statistical Computing.R Foundation for Statistical Computing,Vienna,Austria[EB/OL].URL http://www.R-project.org/,2013.

