基于灰色理論的肥城盆地礦井涌水量預測

卜慶偉，辛宏杰，郭 磊

（山東省水利科學研究院，山東 濟南 250014）

準確預測礦井涌水量的大小是制定最優排水方案，采用最優的防治水害措施，控制礦井水災害事故發生和發展的關鍵。然而，礦井涌水量影響因素眾多，預測難度較大。

目前礦井涌水量預測大體上可分為確定性分析方法和不確定性（隨機）分析方法兩類。相比于確定性分析方法，不確定性分析方法需要的基礎資料相對較少，對礦井用水預測影響因素的處理方法相對簡單。本文把灰色理論應用于肥城盆地礦井涌水量預測，有效解決了地質條件復雜、樣本量小等問題，獲得了較為理想的預測結果。

1 研究區概況

肥城盆地位于魯中南山區，行政上大部分屬于山東省肥城市，主要包括新城、老城、潮泉、儀陽、王瓜店、湖屯、石橫、王莊、桃園等9個鄉鎮，面積約750 km2，人口約60萬。盆地內工礦企業眾多，是泰安市重要的工業基地。

近年來，隨著經濟的發展，水資源消耗量越來越大，而盆地內地表水缺乏，用水主要來自地下水，致使盆地內地下水水位大幅度下降。20世紀80年代以來，肥城盆地地下水水位每年下降1.9～2.4 m不等，這不僅給工農業生產、人民生活帶來重大影響，而且某些煤礦區由于地下水位大幅度下降，加劇了采空區地面的嚴重變形塌陷，帶來一系列環境問題。

與此同時，肥城盆地分布著106 km2的石炭——二迭系煤田，僅礦井排水多年平均就在4 000萬m3左右，這些礦井水僅有10%得到灌溉利用，大部分排入康匯河，并與其他工農業生活污水混流，嚴重污染了當地環境。

2 灰色預測模型建立

灰色系統預測模型是一種全因果模型，其信息內涵豐富，可直接對輸出序列建模，系統變量n取 1，為 GM（1，1）模型。 建立 GM（1，1）模型只需一個數列，即 X（0）為原始數列：

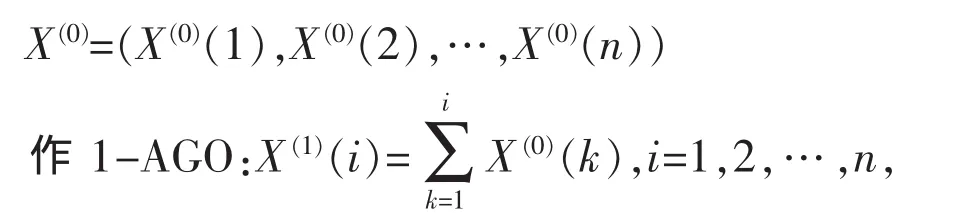
得到新數列：

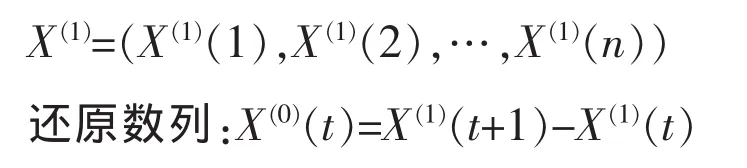
對于GM（1，1）得到的預測值是否可信，需要進行后驗差檢驗。具體檢驗指標包括殘差均值（ε）、后驗差比值（C）、小誤差概率（P）。 根據經驗，一般可按表1劃分精度等級。

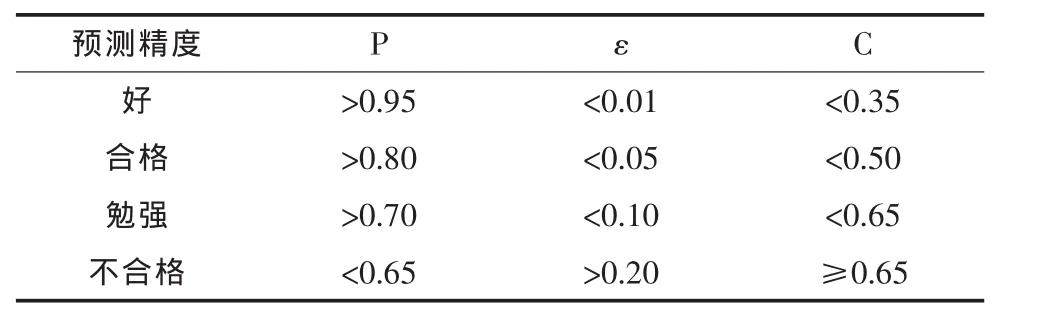
表1 精度判斷表

3 礦井涌水量預測

肥城礦區的歷年涌水量變化見圖1：

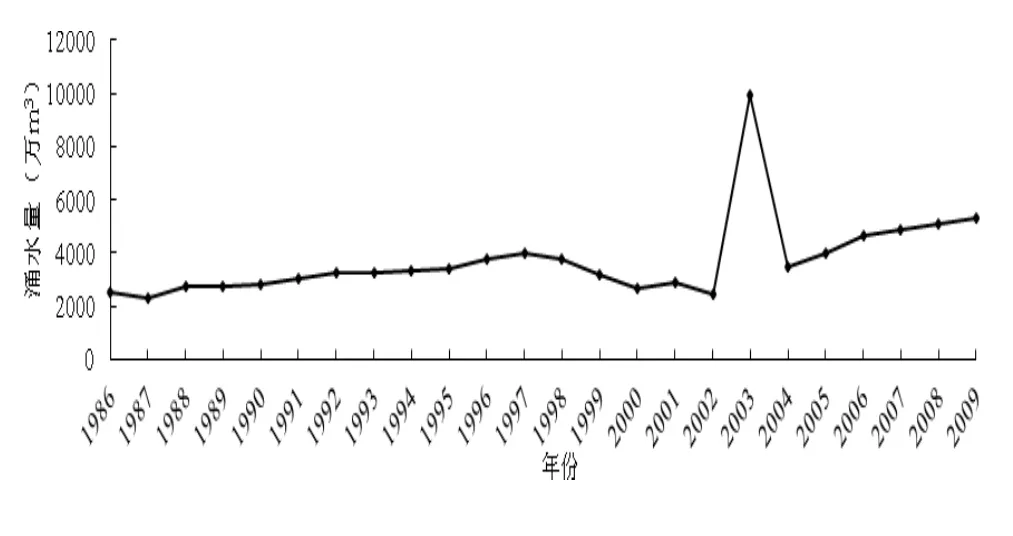
圖1 肥城盆地礦區歷年礦井涌水量變化趨勢圖

從圖1可以看出，1986年以來礦井排水基本穩定。然而，受到復雜水文、地質、氣象、開采情況因素的影響，從上述曲線中很難發現明顯的線性規律，如2003年的突變，資料顯示，為國家莊煤礦8101工作面奧灰水突出導致該年份涌水量突然變大。

根據灰色預測原理，如果對原始數據經過一次1-AGO處理，則可以得到曲線見圖2。原始數據處理后表現出很好的規律，這是因為利用灰色理論對原始數據進行處理后弱化了水文、地質、氣象、開采情況因素對礦井涌水量的影響。

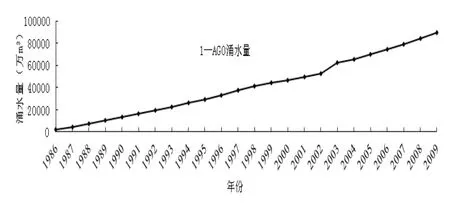
圖2 1-AGO處理后肥城盆地礦區歷年礦井涌水量變化趨勢圖

采用2004—2009年肥城礦區礦井涌水量數據，建立 GM（1，1）模型，通過計算機程序對數據進行擬合，得到的時間響應函數為：

累減得到還原函數為：

=3933.678exp0.06318k

（k=1，2……）

運用還原函數，分別模擬各年份的涌水量，對比模擬值與實際值的殘差，判斷該模型用于下一步預測的可行性，具體數據見表2：

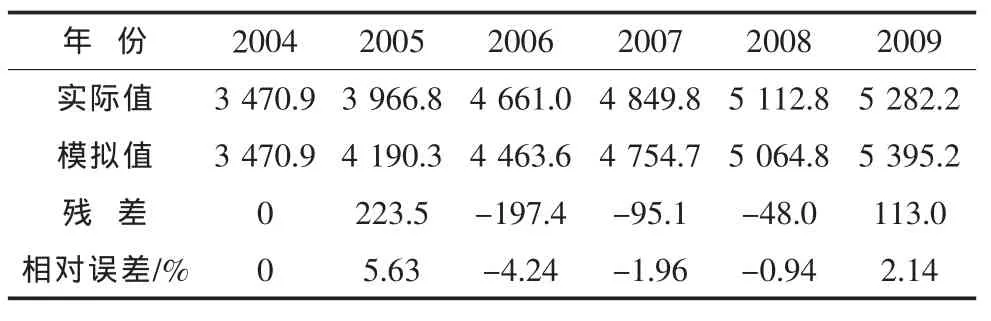
表2 GM（1,1）模型擬合肥城礦井涌水量結果表

由表2知，上述時間相應函數平均相對誤差2.98%，通過后驗差檢驗，該模型P=1，C=0.21<0.35，根據前面介紹模型精度評價指標，該模型為“好”，可以用作下一步的預測，由此函數進行的兩步預測結果分別為：5 747.1、6 121.9。可以看出，未來肥城礦區的礦井涌水還會逐年增加，這對于今后礦井水資源利用工程設計及當地水資源供需分析提供了重要的數據支持。

4 結語

灰色模型用于礦井涌水量的預測，所需數據量小，計算簡便，總體預測精度能夠滿足肥城礦井水資源化利用的要求，相對于其他方法具有明顯的優勢。

GM（1,1）模型預測期不宜過長，超前越遠，誤差越大，這是因為GM（1,1）模型階數低，建模過程計算量小，所以具有實際意義、精度較高的預測值是最近的兩個數據，更遠的數據只反映趨勢值，短期預測具有較大的參考價值。

根據灰色系統理論“新信息優先”的原則，在建立模型時，應該采用較近的數據，同時不斷把新數據添加到建模的時間序列中去，這樣才能保證動態預測的精度。

[1]趙永生.礦井涌水量的灰色-馬爾科夫預測方法[J].工程安全與防塵，1995（8）:10-16.

[2]杜敏銘，鄧英爾，許模.礦井涌水量預測方法綜述[J].地質學報，2009，29（1）：70-73.

[3]鄧聚龍.灰色系統基本方法.武漢[M]：華中理工大學出版社，1988.