基于FLUENT的循環流化床鍋爐冷態流場數值分析

辛凱 孫通 張全厚

（1.哈爾濱電站設備成套設計研究所有限公司，哈爾濱 150046；2.神華（福建）能源有限責任公司，福州 350005；3.北方重工集團有限公司，沈陽 110141）

循環流化床鍋爐是在沸騰爐的基礎上發展起來的，采用循環流化床的燃燒方式運行，簡稱CFB鍋爐，由于其具有燃料適用性廣、煙氣中的污染物排放量低、爐膛內燃燒效率高等顯著的優點，目前已被廣泛投入使用，在未來將向著幾十萬千瓦級的大型化方向發展[1]，在這方面的研究、開發和運行優化方面也日益受到相關專家學者的重視。

爐膛的流場工況在很大程度上影響著鍋爐和電廠整體運行的經濟性、安全性以及設備的壽命，由于鍋爐的燃料性質、設備狀況、工作人員的水平等因素影響鍋爐在理想工況下運行，使得其運行的經濟性、安全性受到一定程度的影響。但在當今的電廠中，由于設備龐大而復雜，運行中可調節的參數較多，試驗不能應對需要而隨時進行，加之參數對與之有關的工況影響已不能憑想象和經驗做出判斷[2]，由此冷態試驗應運而生。

近年來，已有多位學者對鍋爐冷態試驗進行了相關研究，衡麗君、段坤杰等[3]對220 t/h的循環流化床鍋爐進行過冷態試驗分析；張呂鴻、劉萌萌等[4]對二次風入口結構的改進設計進行過研究；湛志鋼、曾庭華[5]對300 MW循環流化床鍋爐進行過冷態試驗分析，并將試驗結果與135 MW等級機組冷態試驗結果進行了對比。由于現場的試驗條件有限、試驗耗費的周期較長等不利因素的影響，循環流化床鍋爐的冷態流場很難得到實時的分析，本文運用大型商用CFD軟件FLUENT，基于Simple算法，運用RNG k-ε湍流方程，結合有限體積法對控制方程進行離散，在一次風速為25 m/s不變的情況下，針對二次風速分別為40 m/s、45 m/s、50 m/s工況下的流場分布進行仿真模擬，并將三種工況下的結果進行對比分析，適時通過試驗來驗證，為循環流化床鍋爐的實際熱態運行提供參考依據。

1 模型的建立

1.1 物理模型

循環流化床鍋爐的物理模型、結構尺寸及一次風、二次風流動方向如圖1所示，采用solidworks軟件生成。

1.2 數學模型

采用FLUENT6.3研究爐膛內的空氣流動，利用gambit軟件建立三維模型和劃分網格，根據模型的特點，選擇六面體網格，數目為76萬，增加兩次網格數目進行無關性檢驗，得出的誤差在合理范圍內，最終計算結果的精確性可得到保證。爐膛內的空氣流動采用RNG k-ε湍流方程求解，壓力速度耦合采用Simple二階迎風的離散化算法，將迭代計算的殘差精度設置為10-5。

RNG k-ε模型是由Yakhot及Orzag提出的，通過大尺度運動和修正后的粘度項體現小尺度的影響，而使這些小尺度運動有系統地從控制方程中去除，所得到的k方程和ε方程，與標準k-ε模型非常相似：

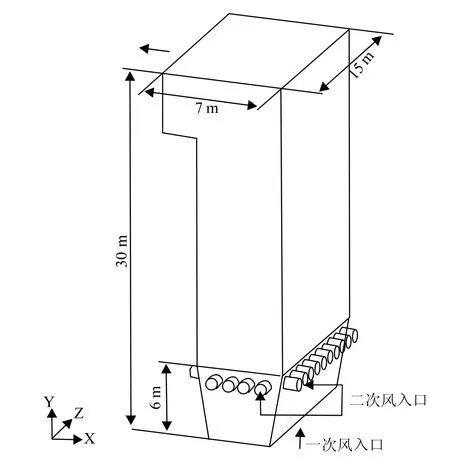
圖1 循環流化床鍋爐的物理模型

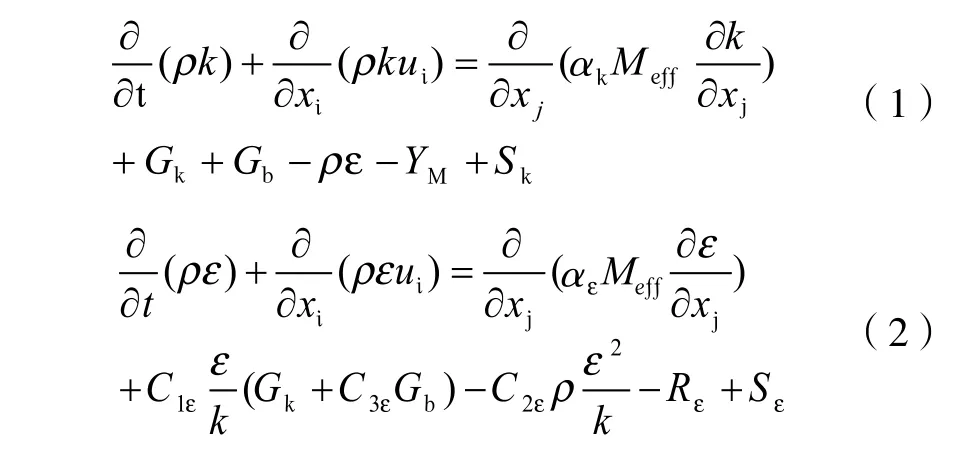
Gk是由層流速度梯度而產生的湍流動能，公式（1）介紹了計算方法；Gb是由浮力而產生的湍流動能，公式（2）介紹了計算方法；YM是由于在可壓縮湍流中，過渡的擴散產生的波動；C1ε、C2ε、C3ε是常量，αk和αε是k方程和ε方程的湍流Prandtl數；Sk和Sε是用戶定義的。

與標準k-ε模型比較發現，RNG k-ε模型的主要變化是：

（1）通過修正湍流粘度，考慮了平均流動中的旋轉及旋流流動情況；

（2）在ε方程中增加了一項，從而反映了主流的時均應變率Eff，這樣，RNG k-ε模型中產生項不僅與流動情況有關，而且在同一問題中也還是空間坐標的函數。

從而，RNG k-ε模型可以更好地處理高應變率及流線彎曲程度較大的流動[6]。

1.3 邊界條件

一次風和二次風的邊界條件均設置為速度入口，其余設置為壁面邊界條件，出口設置為自由出口[7]。

2 結果與分析

2.1 速度場分析

迭代計算收斂后，在z =7.5 m處建立切片，并進行三種工況的對比性能分析，圖2為針對二次風速分別為40 m/s、45 m/s、50 m/s情況下的爐膛流場速度矢量圖。

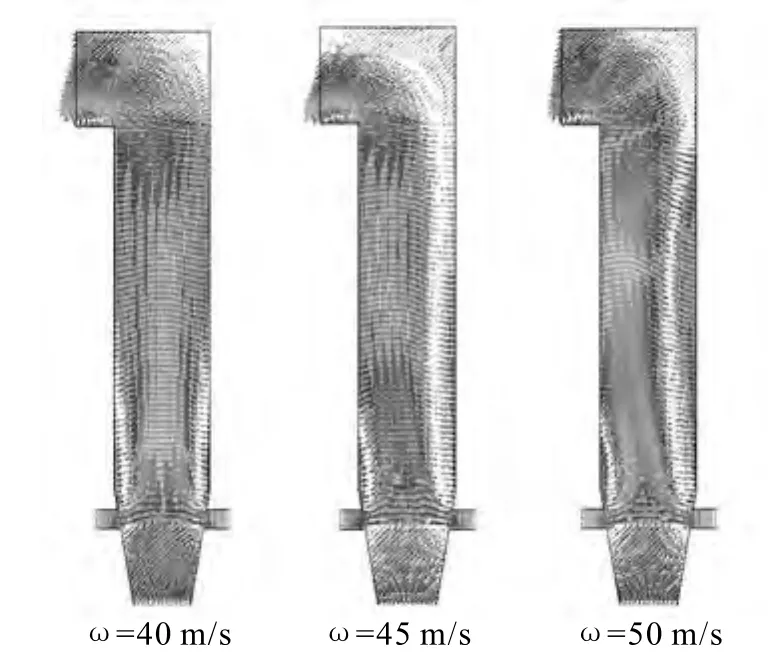
圖2 不同二次風速下的爐膛流場速度矢量圖

由圖2的模擬結果可以看出，在一次風速不變的情況下，當二次風速定為40 m/s時，爐膛內的流場分布較不均勻，邊界處易出現高速流動區域和流動死區，但隨著二次風速的增大，爐膛內的流場分布趨向平穩，分布變得逐漸均勻，這是由于在固定的結構和一次風速不變的前提下，增大二次風速，在一定程度上克服了空氣在爐膛中的流動阻力，使流動更為順暢，邊界處的流動死區減少，可有效減少結垢現象，對提高設備的使用壽命提供保障[8]。

2.2 湍流強度分析

圖3為三種不同二次風速時z =7.5 m截面處的湍流強度分布等值線圖。

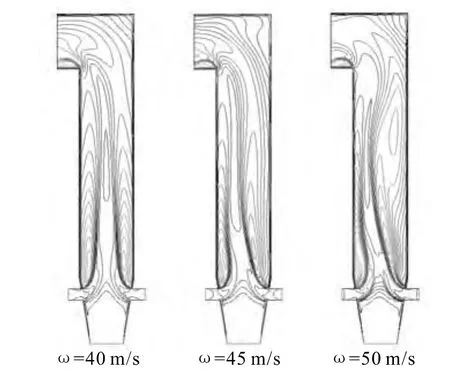
圖3 不同二次風速下的爐膛湍流強度等值線圖

圖3給出了不同二次風速下的爐膛內湍流強度等值線圖，通過對比可以看出，在二次風速為40 m/s時，整體平均湍流強度較小，隨著二次風速的增大，爐膛中的空氣流動變得劇烈，湍流強度增大，這是由于在較低的二次風速下，空氣的流動處于較弱的湍流狀態。

3 試驗分析

為驗證模擬的精確性，在現場進行冷態試驗分析[9]，在爐膛中取10個測點，同樣保持一次風速恒定不變，二次風速分別設置為40，45，50 m/s，每個測點間隔3 min后，取一組數據，接連取5組，計算平均值，與FLUENT中的計算數據進行對比，擬合出曲線圖4、圖5、圖6。

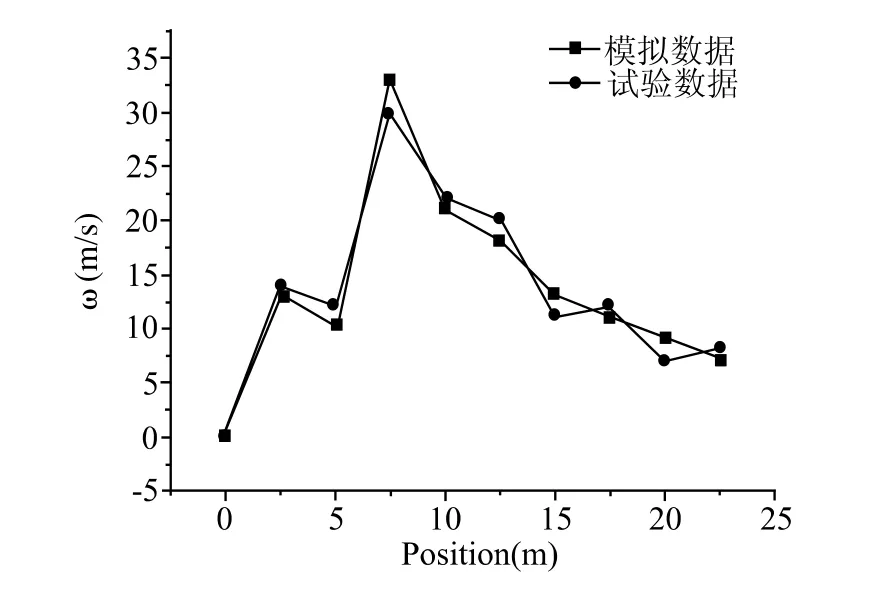
圖4 二次風速為40 m/s時的模擬與試驗結果對比

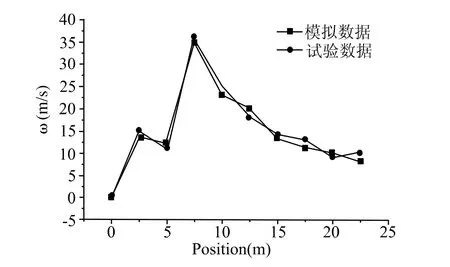
圖5 二次風速為45 m/s時的模擬與試驗結果對比

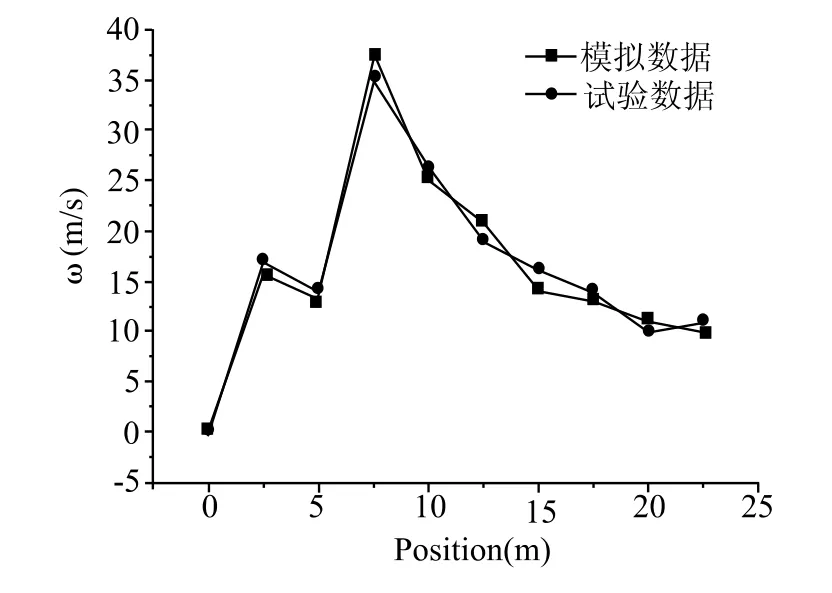
圖6 二次風速為50 m/s時的模擬與試驗結果對比

由圖4至圖6可以看出，FLUENT的模擬計算值與實測值的擬合曲線分布趨勢較為吻合，誤差在允許范圍內，尤其是臨近爐膛空氣出口處，其誤差主要是由于測量系統偏差、人為操作、模型的簡化處理等不可避免的原因引起的[10]。

4 結論

（1）本文根據現場的運行工況和循環流化床鍋爐的實際尺寸，建立出模型，采用FLUENT軟件對調整二次風速后的流場變化進行了分析，解決了試驗條件有限、不能適時進行的問題。

（2）通過后續的試驗對比分析，可見模擬結果的精確性可靠，可作為循環流化床鍋爐實際熱態運行的參考依據。

（3）一次風速恒定不變，隨著二次風速的增大，爐膛中的流場趨近平穩，但綜合考慮爐膛總風壓與燃燒充分性等因素，一、二次風的配比需合理，在實際運行中應酌情考慮。

[1] Yue G X，Yang H R，Lu J F，et al. Latest development of CFB boilers in China[C]//Proceedings of the 20th International Conference on Fluidized Bed Combustion, Springer, 2010.

[2] 廖宏楷，王力. 電站鍋爐試驗[M]. 中國電力出版社，2007.

[3] 衡麗君，段坤杰，何長征. 220t/h鍋爐冷態數值試驗研究[J]. 熱能動力工程，2006,21(6)：573-577.

[4] 張呂鴻，劉萌萌，孫永利, 等. 基于CFD的循環流化床鍋爐二次風入口結構的改進設計[J]. 化工進展，2013,32(10):2518-2522.

[5] 湛志鋼，曾庭華. 300MW循環流化床鍋爐冷態試驗[J]. 鍋爐技術，2009,40(6):37-40.

[6] 王福軍 計算流體動力學分析-CFD軟件原理與使用[M]. 清華大學出版社，2004.

[7] 肖琨，王強，劉富君. 基于Fluent的某型號鍋爐末級過熱器流動特性數值研究[J]. 能源工程，2011(3):9-13.

[8] 葉江明. 電廠鍋爐原理及設備[M]. 中國電力出版社，2007.

[9] 王鵬利，趙小兵，李連友. 循環流化床鍋爐冷態試驗方法[J]. 熱力發電，2007(10):27-29.

[10] Zeng Tinghua, Zhan Zhigang. Deep Desulphurization and DeNOx in Circulating Fluidized Bed Boiler[J]. Electricity, 2011,(5):46-49.