基于ANSYS的齒輪靜態有限元分析

熊艷紅 朱志強

(湖北職業技術學院，湖北 孝感 432000)

0 前言

齒輪傳動是機械傳動中機械原理和機械設計的精髓，它具有效率高、結構緊湊、工作可靠、壽命長等優點。但在齒輪傳動中，輪齒由于齒根彎曲疲勞載荷而發生齒根彎曲折斷，因此，對齒輪要進行齒根彎曲強度計算。傳統的手工齒根彎曲疲勞強度計算帶有很大的近似性，且計算過程比較繁瑣，所以，采用新的方法來分析齒輪彎曲強度勢在必行！隨著計算機技術的普及和發展，有限元法在齒輪設計和應力分析中已顯示出巨大的優勢。目前較典型的有限元分析軟件，ANSYS計算過程自動化，在后處理中能快速、直觀、精確地觀察到計算結果，這些都是手工和實驗方法無法比擬的，它可以有效地分析齒輪接觸應力和變形，有效地計算摩擦接觸問題[1]。人們對齒輪進行手工計算分析已經相當深入，但借助計算機對齒輪靜態分析卻很少，本文將運用ANSYS對直齒圓柱齒輪進行靜態分析，得出了齒輪的最大應力、最大應變和變形云圖。

1 創建有限元模型

1.1 模型的建立

鑒于漸開線為極坐標方程形式，為便于幾何建模，在ANSYS中,首先選擇總體坐標系為柱坐標系，利用漸開線的極坐標方程式得到漸開線上點的坐標,在ANSYS下生成相應的關鍵點。然后再利用ANSYS中的樣條曲線功能即可生成所需曲線,從而實現輪齒模型的建立。

在當前坐標系下建立關鍵點：1(5.428，76.307)、2(5.534，77.803)、3(5.595，79.303)、4(5.411，80.82)、5(5.11，82.342)、6(4.694，83.869)、7(4.208，85.396)、8 (3.623，86.92)、9 (2.928，88.45)、10 (2.214，89.972)、11(0，90)，利用樣條曲線功能依次連接關鍵點1至10形成漸開線輪齒的外輪廓線，然后鏡像生成另一邊的輪廓線，如圖1。生成圓環面，內徑15mm，外徑76.5mm，顯示線，在齒輪的軸線上建一條直線，沿該直線由延伸成體的命令得一三維實體模型。

1.2 定義單元類型和材料屬性

在對模型進行網格劃分之前，要定義所需要的單元類型。不同的單元類型會直接影響網格劃分以及最終求解的效果。對二維單元選用shell的Elastic 4node 63，對三維單元選用Solid的Brick 8Node 45。本文是基于對一個齒輪的研究來模擬兩個相同齒輪的嚙合，所以只定義一個齒輪的材料屬性[2]。由于所選齒輪的材料為常用的45號鋼，其各屬性為：彈性模量 E=2×108Pa，泊松比 v=0.3，密度 Density＝7.8×103kg/m3。

1.3 約束和載荷

對二維、三維實體模型的劃分均采用自由劃分，將齒輪中心孔處固定，使其在x，y，z方向均不產生位移，并約束其繞x，y和z軸的旋轉。由于選擇的單元類型為二維實體42號單元，只具有x和y方向的平移自由度，所以在DOFs to be constrained一欄中直接選All DOF即完成了約束的施加。

齒輪傳動的輸入功率P=7.93kW，小齒輪轉速n=960r/min，小齒輪的分度圓直徑為168mm，由 (1—4)式計算出主動輪傳遞的轉矩T=95.5×105P/n=95.5×105×7.93/960=78934.8N·mm， 圓周力 Ft=2T1/d1=2×78934.8/168=939.7N，徑向力 Fr=Ft×tanα=939.7×tan20=342N。

式中：P——齒輪傳遞的功率，單位為kW；

n——齒輪轉速，單位為r/min；

T1——小齒輪傳遞的轉矩，單位為N·mm；

d1——小齒輪節圓直徑，對標準齒輪即為分度圓直徑，單位為mm；

α——嚙合角，對標準齒輪，α=20°。

2 齒輪的靜態分析

在靜力學分析中，齒輪通過鍵聯接在軸上，通過外界輸入轉矩使齒輪與軸一起轉動。外載荷作用在與端面平行的平面內，設沿齒厚方向均勻分布，故可簡化為平面問題處理。其加載處理后的應力應變圖和位移圖如圖1，2，3，4，5。從圖1中可以看出x方向最大應力出現在嚙合輪齒被拉伸一側的齒根部分，齒根部分的應力分布從大到小漸變。比較圖1和圖2可以看出，輪齒上同一地方，y方向應力比x方向的小，這是因為y方向的力較小。齒根部分的應力分布從大到小漸變。從圖3中可以看出，剪切應力分布大致均勻對稱，最大應力同樣出現在輪齒齒根部分。在圖4中，應力最大的齒根部分應變也最大，從齒根部分向里，應變是從大到小漸變的。由圖5可以看出，從軸孔到捏合的輪齒齒頂的徑向，位移從零開始越來越大。齒輪的最大位移發生在齒頂，輪齒的位移方向與法向載荷方向一致。由于軸孔周圍施加約束及材料的剛度的影響，其位移為零。

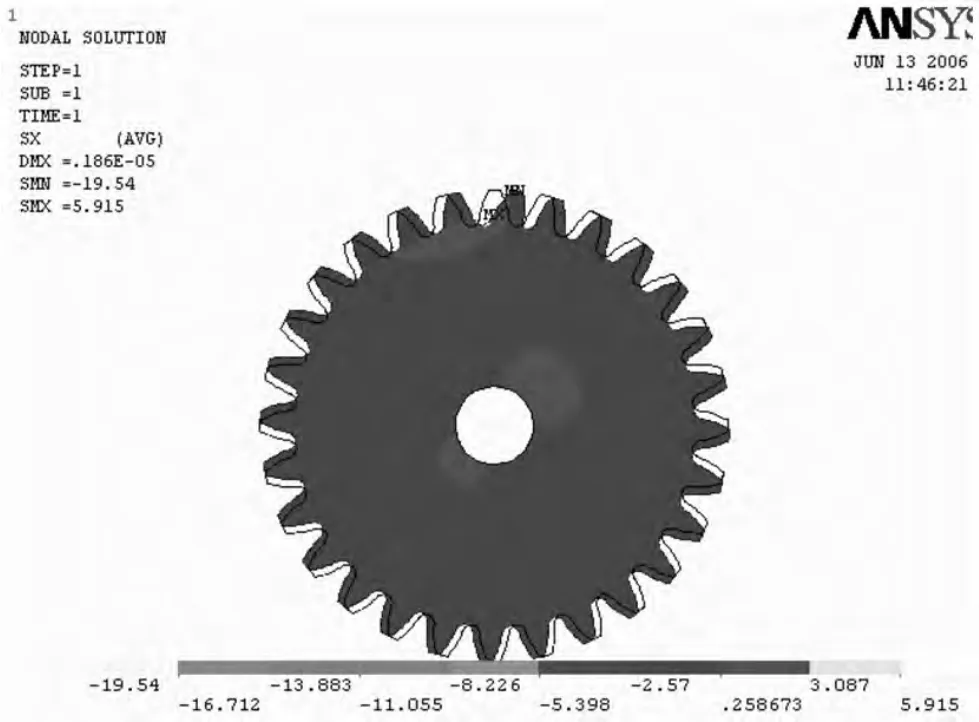
圖1 X方向應力

3 結論

用ANSYS軟件對齒輪進行靜態分析，可迅速準確的得出結果，該結果與傳統方法計算的結果相差很小并偏向保守，由模擬結果表明：齒輪的失效首先在齒根出現，利用所得結果可進行齒輪齒根彎曲疲勞強度以及齒面接觸疲勞強度校核，為齒輪傳動的優化設計提供了基礎理論。

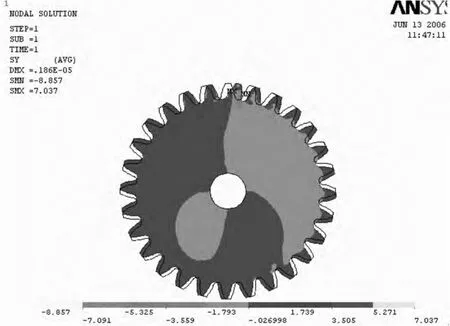
圖2 Y方向應力

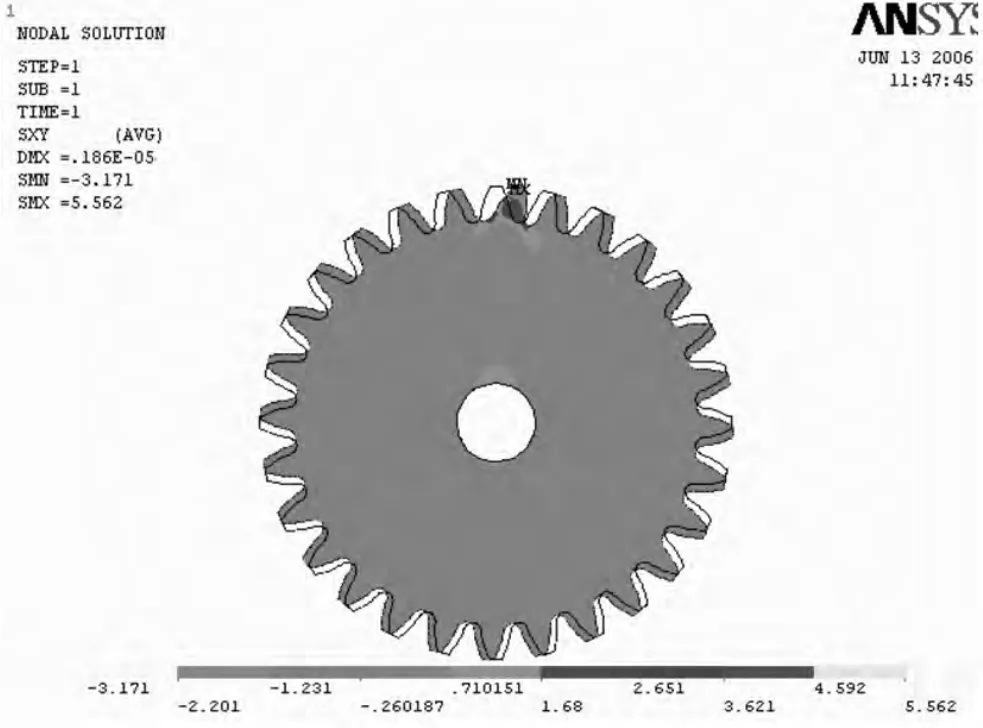
圖3 XY方向剪切應力

圖4 應變云圖

圖5 變形前后的位移云圖

[1]仙波正壯.高強度齒輪設計[M].北京:機械工業出版社,1991：1-124.

[2]包家漢，張玉華，薛家國，等.基于ANSYS的齒輪參數化建模及其應用[J].安徽工業大學學報，2005,22(1)：35－38.