枯草桿菌蛋白酶嗜熱性改造單突變效果評判方法研究

夏 翾，馬 帥，王 勤，李曉琴

(北京工業大學生命科學與生物工程學院，北京100124)

蛋白酶是一種天然的生物催化劑，具有較高的催化效率和底物特異性，被廣泛應用于工業、食品業、醫藥業及人們的日常生活中［1-2］。蛋白酶發揮其高活性和高催化性是需要特定的條件作為保障的，如適當的PH值、溫度、離子濃度等［3］。其中，溫度這一因素尤為重要。蛋白酶只有在一定的溫度范圍內才能保持較高的活性，超出了這個溫度范圍，酶的活性就會降低甚至消失，嚴重影響它們的實際應用。因此，了解蛋白酶的熱穩定機制進而提高蛋白酶的熱穩定性［4］，對擴大酶的應用范圍與探究蛋白質結構和功能關系均具有非常重要的意義。

蛋白質的熱穩定性是由多種作用共同參與的，不同的蛋白質可能有不同的耐熱機制，在這些作用中比較重要的有:氨基酸組成、氫鍵、鹽橋、疏水作用、包埋效應、環和N、C端的穩定性等［5］。目前，提高枯草桿菌蛋白酶熱穩定性的方法主要有兩種，一種是改變酶的催化環境，如調節PH值、增加有機溶劑、底物保護等，這種方法不能從本質上改變枯草桿菌蛋白酶的耐熱性，因此在工業應用上會受到很多的限制;另一種是對蛋白酶進行殘基突變，在蛋白質的薄弱環節引入有利殘基，加強局部或整體的彼此相互作用，從而增加蛋白的熱穩定性。

殘基突變是提高蛋白酶熱穩定性的有效方法，如何評判殘基突變對蛋白酶熱穩定性的影響?目前，對蛋白酶嗜熱性突變效果的判定主要有兩種方法，一種是生物實驗的方法［6］，即將突變成功的蛋白通過蛋白質合成技術制造出來，然后通過逐漸升溫來驗證其突變效果的優劣。該方法有較高準確性與可靠性，但是會耗費大量的時間和人力。另一種是生物信息學計算的方法［7-9］，即計算ΔΔGu值來評定嗜熱性突變的效果。ΔGu(蛋白質解折疊自由能)是蛋白質熱動力學參數中最重要的參數，也是反應蛋白質熱穩定性的一個通用指標，因此多數方法都是利用生物信息學計算的方法來模擬突變前后ΔGu的變化，即ΔΔGu(式1)。當ΔΔGu＞0時，表明該突變對蛋白質的熱穩定性有正效應(即嗜熱性突變效果好)，反之有負效應(即嗜熱性突變效果差)。

2005年，Korkegian等直接從蛋白質結構入手預測蛋白質的ΔGu，該方法主要是利用一些經驗數據或方法來分析蛋白質突變前后其結構或能量變化，來推斷其 ΔGu的變化［10］。2006年，Saraboji等利用統計數據分析預測蛋白質的ΔGu，即用一些統計學的手段對突變體數據進行分析，得到一些統計學的規律，以此來判定突變前后的 ΔΔGu［11］。2008 年，Capriotti等提出機器學習方法，即利用蛋白質的序列或結構特征直接從數據入手，建立計算模型來預測ΔΔGu［12］。該方法較生物實驗方法節約了時間和人力，但是其仍具有計算復雜、計算量大的缺點。

分子動力學(MD)模擬是研究蛋白質動力學性質進而揭示其生物學功能的重要工具，利用MD模擬結果提取有效參數、建立蛋白酶嗜熱性改造突變效果評判方法是本文研究的重點。本文以研究資料頗為豐富的枯草桿菌蛋白酶BPN＇為研究對象，選取實驗上已證明的能提高其熱穩定性的突變體來進行研究，運用分子動力學模擬的方法，通過對突變前后蛋白質多種能量參數的對比分析，提取了多個有效參數，并進一步建立了枯草桿菌蛋白酶嗜熱性改造單突變效果評判方法。

1 材料

1.1 枯草桿菌蛋白酶

枯草桿菌蛋白酶是芽孢桿菌屬細菌所分泌的胞外堿性蛋白酶，屬絲氨酸蛋白水解酶類［13-16］。它催化水解蛋白質為氨基酸，在有機溶劑中也能催化多肽的合成。常見的枯草桿菌蛋白酶有 BPN＇、Carlsbery、E、Savinase、BL 等，它們的一級氨基酸序列非常類似，晶體結構也基本相似［17］。枯草桿菌蛋白酶BPN＇與E的區別是43個氨基酸殘基發生替換，Carlsberg與E在序列上的區別是89個氨基酸殘基替換再加上第56位殘基缺失，BL與BPN＇的區別是在275個氨基酸殘基上有103個殘基替換再加上4個殘基(160～163)缺失。

枯草桿菌蛋白酶具有重要的應用價值，被廣泛應用于洗滌劑、制革及絲綢等工業;此蛋白的結構與功能研究已有較長的歷史，其蛋白結構、生化特性、催化機理等均有了較清晰的闡釋。目前，在該酶的嗜熱性改造方面有豐富的突變資料可供參考;另外，解析度為1.8 ?的該蛋白酶的晶體結構數據可以從PDB數據庫中獲取。基于以上原因，我們將枯草桿菌蛋白酶作為研究對象。

以枯草桿菌蛋白酶BPN＇作為研究對象，它共有275個殘基，空間結構如圖1所示。

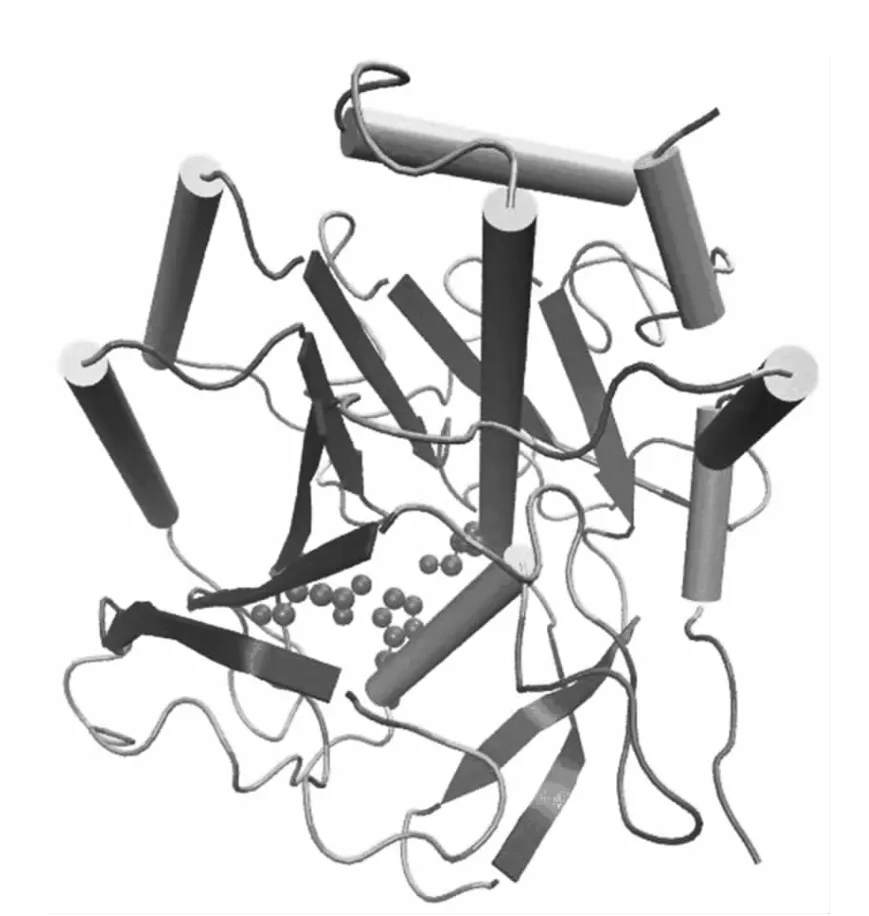
圖1 枯草桿菌蛋白酶空間結構Fig.1 Spatial structure of Subtilisin BPN'

圖中桶狀結構代表α螺旋，固形箭頭代表β折疊，小球代表催化三聯體(Asp32、His64和Ser221)。圖中可見β折疊位于蛋白質內部形成疏水核心，α螺旋位于結構表面，圍繞在β折疊周圍，整個蛋白質呈一個球狀。

1.2 枯草桿菌蛋白酶突變位點的選取

選取6個實驗上已證明的能提高蛋白質熱穩定性的突變點作為研究對象，它們分別為:S161C、G166R［18］、G169A［19］、S188P［20］、K213R［21］以 及P239R［22］。表1為野生型枯草桿菌蛋白酶 BPN＇及其6個突變體的Tm值及60℃下的半衰期時間，這兩個值越大說明結構的熱穩定性越強。由表中數據可以看出，六個突變體的熱穩定性均強于野生型。表中Wild代表野生型枯草桿菌蛋白酶。

2 方法

2.1 枯草桿菌蛋白酶突變體的同源模建

從PDB數據庫中下載解析度為1.8 ?的枯草桿菌蛋白BPN＇晶體結構(PDB:2SIC)，將此結構的E鏈作為野生型樣本。利用SWISS-MODEL進行同源模建，得到表1所列的6個突變體的結構。

表1 枯草桿菌蛋白酶及其突變體的信息統計Table 1 Information statistics of subtilisin BPN'and its mutants

利用野生型及6個突變體的結構信息，分別計算主鏈結構的二面角，繪制圖2所示的拉氏構象圖。圖A為野生型蛋白的拉氏構象圖，圖B、圖C、圖D、圖 E、圖 F、圖 G 分別為 S161C、G166R、G169A、S188P、K213R、P239R突變體的拉氏構象圖。圖中黑色區域表示構象允許區域，在該區域內的任何成對二面角所規定的構象都是立體化學所允許的。灰色區域表示不完全允許區，表示在這個區域內的二面角所規定的主鏈構象雖然是立體化學可允許的，但是不夠穩定，白色區域是不允許區域。在圖中可以看到，構象角絕大部分都處于構象允許區域內，說明這些突變體的構象均處于合理的狀態。

圖2 枯草桿菌蛋白酶及其突變體所對應的拉氏構象圖Fig.2 The ramachandran figure of subtilisin BPN'and its mutants

2.2 分子動力學模擬實驗的設計

使用NAMD軟件對野生型和6個突變體蛋白進行分子動力學模擬，選用CHARMM27全原子力場。預處理過程中，首先刪掉晶體中的氫原子，再使用VMD軟件自帶的psfgen程序包補足氫原子，測得該晶體結構的凈電荷為零;然后給該結構添加一個厚度為10 ?的TIP3P型水分子層，最終得到的水盒子的尺寸是 65 ? ×66 ? ×68 ?。

預平衡過程中，選用NPT系綜。在1個標準大氣壓下，使用SHAKE算法約束氫鍵鍵長，截斷半徑為12 ?，非鍵相互作用在14 ?處截斷。對1個野生型及6個突變體共進行了以下4次分子動力學模擬過程:

(1)溫度恒定為370 K，步長為2 fs/step，運行100 000步，分子動力學模擬時間為0.2 ns，此過程命名為370 K_0.2 ns;

(2)溫度恒定為370 K，步長為2 fs/step，運行1 000 000步，分子動力學模擬時間為2 ns，此過程命名為370 K_2 ns;

(3)溫度恒定為370 K，步長為1 fs/step，運行100 000步，分子動力學模擬時間為0.1 ns，此過程命名為370 K_0.1 ns;

(4)初始溫度為300 K，步長為2 fs/step，運行100 000步，每2 000步升高1 K，終止溫度為350 K，分子動力學模擬時間為0.2 ns，此過程命名為300 K_0.2 ns。

其中370K_0.2ns作為標準組，其他3組作為對照組。

2.3 基于模擬結果的參數計算

每個野生型及其突變體分子動力學模擬完成后均輸出一個“.log”日志文件，包含了模擬過程中的壓力、溫度以及本實驗中需要用到的能量等信息。配置文件中設置每1 000步(即2 ps)輸出一次能量信息，而我們需要計算的是在模擬的整個過程中或者某一特定時間段內的平均能量，因此具體方法如下:利用VMD軟件的能量計算腳本 namdstats.tcl，結合輸出的.log日志文件，提取蛋白體系的以下平均能量信息:BOND(鍵能)、ANGLE(鍵角能)、DIHED(二面角能)、ELECT(靜電能)、VDW(范德華力能)、KINETIC(動能)。

3 結果與分析

3.1 模擬結果

依照上述方法，我們共得到4組動力學模擬后的能量結果(見表2～表5)。每組表格中上半部分為提取的能量值，下半部分為每個突變體與野生型能量的差值以及能量的變化趨勢。

首先，以溫度為1個標準大氣壓下溫度為370 K、時間為0.2 ns的模擬作為標準組。表2是該組的模擬能量結果，我們提取的是每個結構從模擬第一步到最后一步的能量平均值。由表中數據可以看出，6個突變體與野生型酶相比，每種平均能量值均出現了相同的變化趨勢，即 BOND增大、ANGLE增大、DIHED減小、ELECT減小、VDW 增大、KINETIC增大。

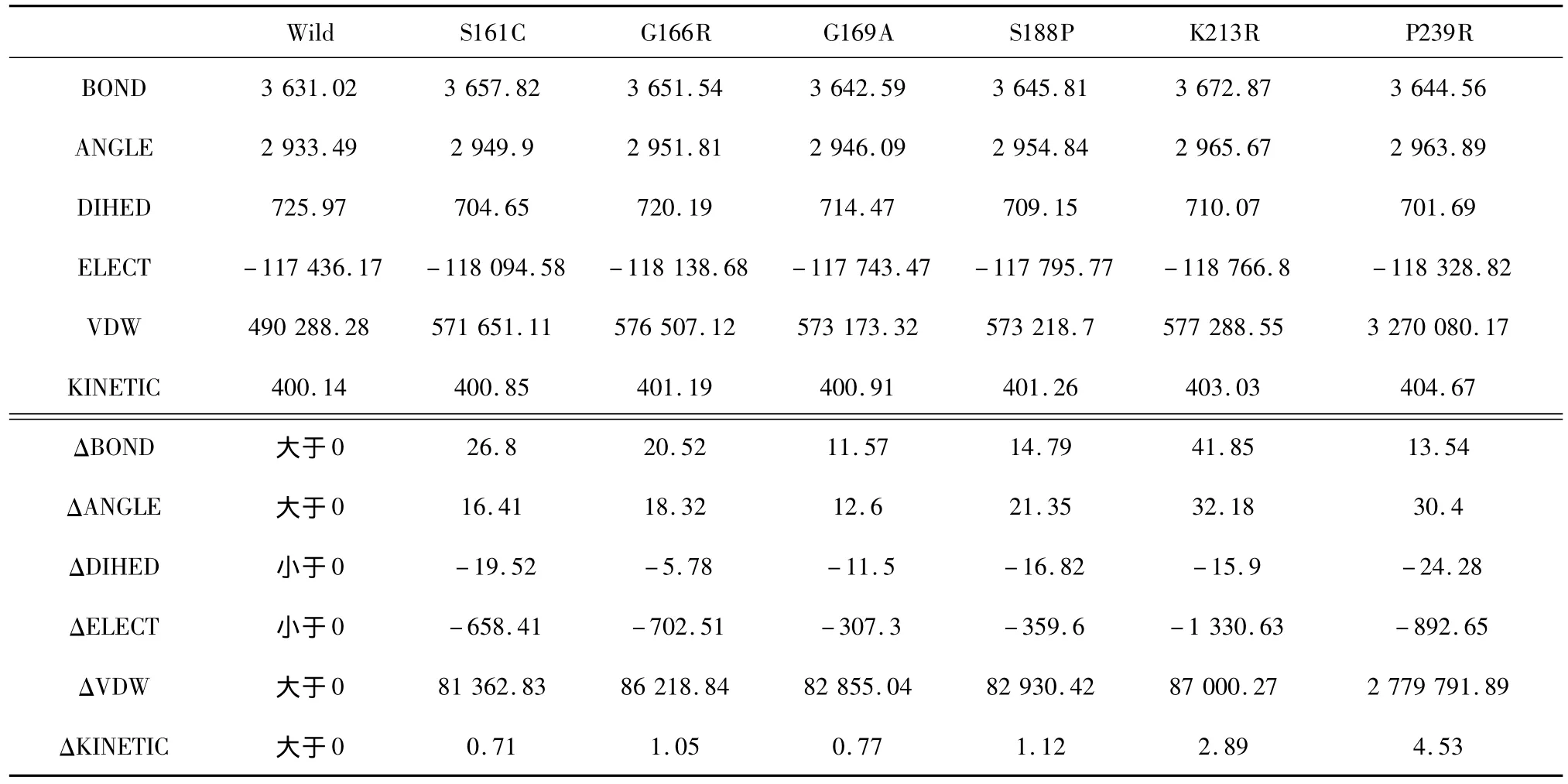
表2 370 K_0.2 ns模擬平均能量(kcal/mol)Table 2 Average energy data simulated-370 K_0.2 ns(kcal/mol)

標準組的模擬溫度為370 K，模擬時間為0.2 ns，這樣高溫、短時間的模擬并沒有使野生型及突變體動力學模擬達到平衡，為了檢驗非平衡態的能量統計結果的可靠性，我們在標準組370 K_0.2 ns模擬的基礎上進行了較長時間的模擬，溫度不變，模擬時間增加為標準組的10倍，即2 ns。圖3為該模擬下野生型及其突變體的RMSD曲線圖。可以看到，在1.0 ns～1.5 ns的時間段，7個結構的RMSD曲線均呈現平穩狀態，說明在此時間段內達到了平衡狀態。因此我們提取了這段時間內的能量平均值，并計算突變體與野生型的能量差值(見表3)。可以看到，表中突變體的6種平均能量值有著與標準組相同的變化趨勢。

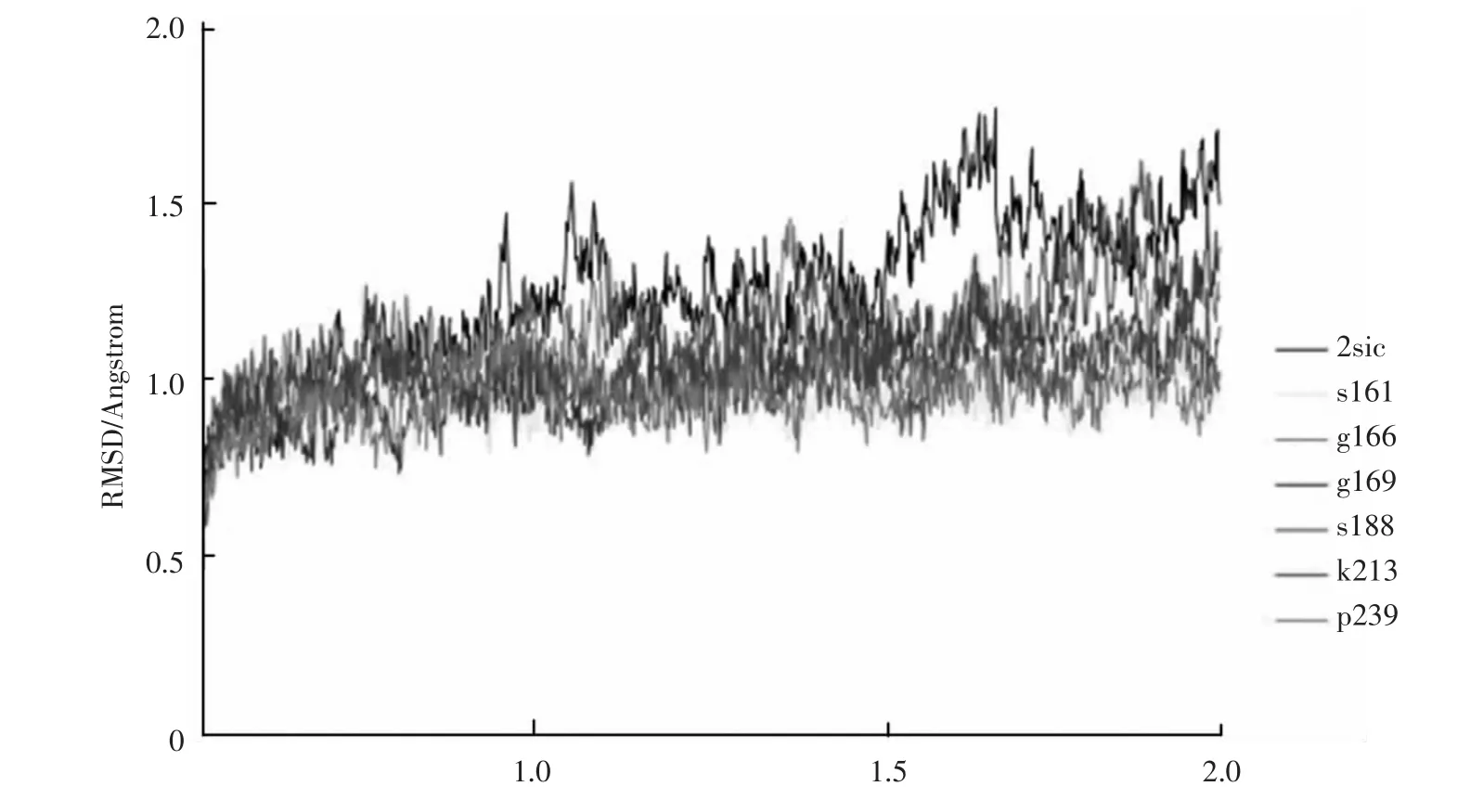
圖3 枯草桿菌蛋白及其突變體2ns分子動力學模擬過程中的RMSD曲線Fig.3 The RMSD curves ofSubtilisin BPN'and its mutants in 2ns in the molecular dynamic simulation

表3 370 K_2 ns模擬平均能量差值(kcal/mol)Table 3 D-value of average energy data simulated-370 K_2 ns(kcal/mol)

從表2、表3的結果看，模擬時間的長短以及體系是否平衡對能量變化趨勢并沒有影響，為進一步檢驗模擬時間對結果的影響，我們在溫度不變的情況下，進行了更短時間的模擬，模擬時間縮減為標準組的一半，即0.1 ns，其能量差值見表4。表4中所有能量的變化都較標準組呈現相同的趨勢。

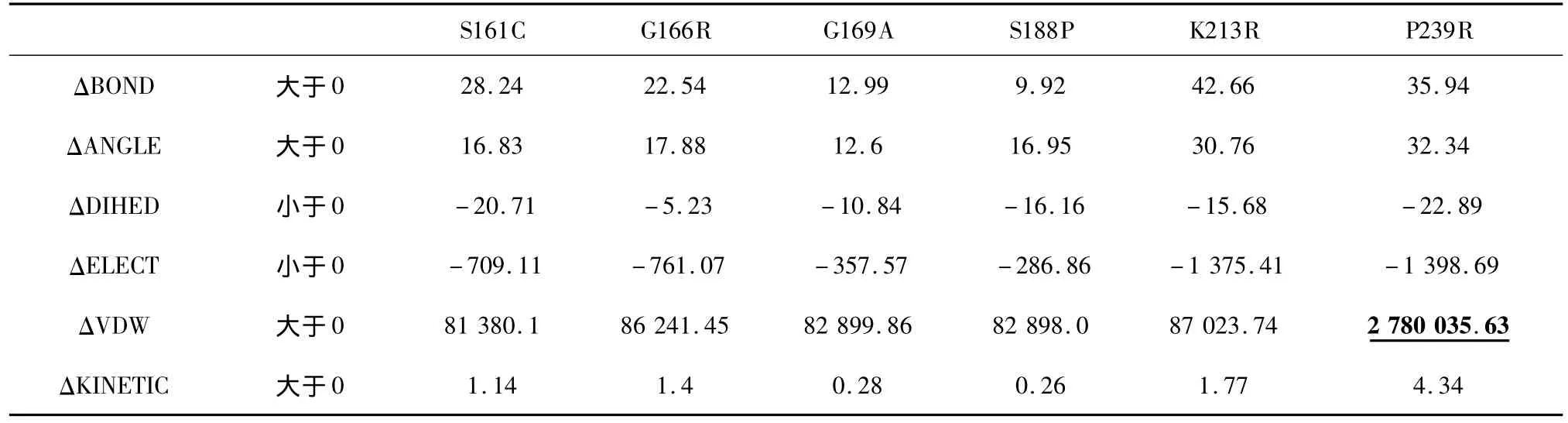
表4 370 K_0.1 ns模擬平均能量差值 (kcal/mol)Table 4 D-value of average energy data simulated-370 K_0.1 ns(kcal/mol)

最后，我們檢驗了溫度對模擬結果的影響。在標準組的基礎上我們做了一組溫度均勻變化的模擬300 K_0.2 ns，時間同標準組設置一樣，模擬過程中將溫度從300 K均勻升高到350 K。能量差值結果見表5。由表中數據可以看出，在溫度變化的模擬條件下突變體的平均能量還是出現了與標準組一樣的變化趨勢。

表5 300 K_0.2 ns模擬平均能量差值 (kcal/mol)Table 5 D-value of average energy data simulated-300 K_0.2 ns(kcal/mol)

3.2 結果分析

從上面4個表可以看出，突變體與野生型酶相比，均出現了BOND增大、ANGLE增大、DIHED減小、ELECT減小、VDW增大、KINETIC增大的趨勢。研究表明，分子柔性的降低會帶來嗜熱性的增強［23］，因此突變體的分子柔性均低于野生型，正是由于柔性降低、剛性增強，所以會使得BOND(鍵能)增大、ANGLE(鍵角能)增大以及 DIHED(二面角能)減小;而所有突變體的ELECT(靜電能)都比野生型小，這與以前的實驗中所說引入帶電殘基增強蛋白質熱穩定性是相一致的，靜電能越小穩定性越強［24］;而VDW(范德華能)增大說明分子的極性也增大了，表明蛋白質的嗜熱性與分子極性也密切相關;突變體的KINETIC(動能)雖然比野生型都有所增大，但變化范圍很小，說明這個能量可能與熱穩定性的關系并不大，但我們仍暫時保留這一項，等待后續實驗進行進一步驗證。

另外可以看到表中有一些數據與其他數據相差較大，我們將這些數據稱為極端數據，并用特殊格式將這些極端數據標記出來。除去這些極端數據，我們得到以下突變體與野生型相比的能量變化范圍(單位:kcal/mol):ΔBOND 為［ 2.66，8.57］，ΔANGLE 為［3.32，32.18］，ΔDIHED 為［-16.68，-2.66］，ΔELECT 為［-1 375.41，-286.86］，ΔVDW 為［81 362.83，87 027.74］，ΔKINETIC 為［0.26，2.89］。

為進一步分析能量變化與蛋白嗜熱性的關系，我們利用SPSS分析軟件分別對以上4組模擬中每個突變體的6種能量差值與其對應的Tm或半衰期進行了斯皮爾曼(Spearman)相關性分析，99%置信度下的雙側檢驗的計算結果見表6，其中表的上半部分是G166R、G169A、S188P的Tm值與各個能量差值的絕對值之間的相關系數，下表下半部分是S161C、K213R、P239R的Half life與各個能量差值之間的相關系數。相關系數越大表示相關性越顯著，正數表示正相關，負數表示負相關。

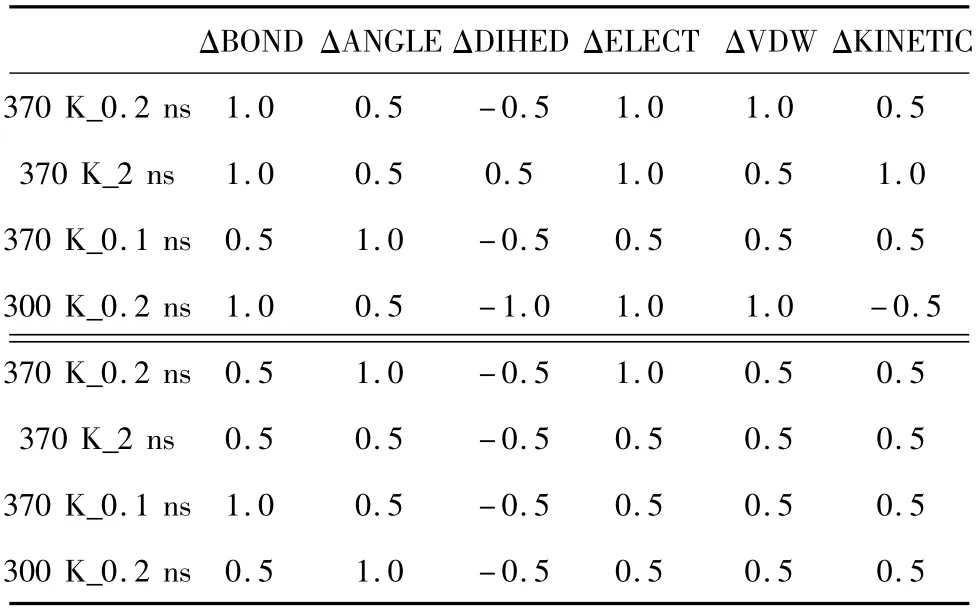
表6 能量差值與TmHalf life的相關系數Table 6 The correlation coefficient between the energy difference and TmHalf life

從表6可以看出:ΔBOND、ΔELECT與突變體的Tm相關性最強，3組模擬時間大于0.1 ns的相關系數均為1，同時與突變體的半衰期也分別有一組相關系數為1，總體平均值為0.75。說明 ΔBOND、ΔELECT對Tm及半衰期的變化最為敏感;ΔANGLE略低于ΔBOND、ΔELECT與突變體的Tm及半衰期的相關性，相關系數為1的共有 3組，平均為0.687 5;ΔVDW與突變體的Tm及半衰期的相關系數均為正值，有兩組模擬時間大于0.1 ns的相關系數為1，總體均值為0.5，相關性一般;而ΔDIHED和ΔKINETIC與突變體的Tm及半衰期的相關性不穩定，說明ΔDIHED和ΔKINETIC對Tm及半衰期的變化趨勢不敏感。

3.3 判定方法

從以上分析可以看出，在4組不同條件的模擬過程中，突變體的6個平均能量值與野生型相比均出現了相同的變化趨勢，結合相關性的計算結果，ΔBOND、ΔELECT、ΔVDW、ΔANGLE、ΔDIHED、ΔKINETIC可以作為評判枯草桿菌蛋白酶嗜熱性改造單突變效果評判的6個有效參數，其中ΔBOND、ΔELECT、ΔANGLE、ΔVDW 為特征有效參數，并采用370 K_0.2 ns模擬結果來提取上述參數。

枯草桿菌蛋白酶嗜熱性改造單突變效果評判方法為:以標準組370 K_0.2 ns的模擬條件參數為準，分別對需要判定嗜熱改造效果的突變體及野生型進行分子動力學模擬，利用模擬結果計算上述4個特征有效參數，如果ΔBOND、ΔVDW、ΔANGLE大于0，同時ΔELECT小于0，則可以判斷該枯草桿菌蛋白酶突變體嗜熱性提高，為有效突變，否則為無效突變。

4 檢驗與討論

4.1 枯草桿菌蛋白酶其他突變點檢驗

我們從Protherm數據庫中選定了2個實驗上已經獲取的枯草桿菌蛋白酶嗜熱突變體作為檢測樣本，它們分別是Q206C和N218S。野生型及2個突變體在ProTherm數據庫的記載見表7。表中2個突變體的Tm值都大于野生型，說明突變體的嗜熱性要強于野生型。另外我們還選取了一個穩定性小于野生型的突變體P239G，實驗測得此突變體在60℃時的半衰期比野生型減少了8.5 min。

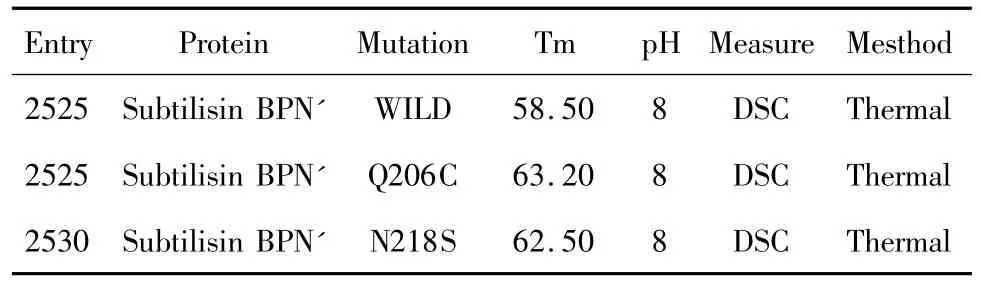
表7 枯草桿菌蛋白酶及其嗜熱突變體在Protherm數據庫中的記錄Table7 Records of subtilisin BPN'and its mutants in protherm

根據3.3節提出的判定原則，我們對以上選取的兩個有效突變體、一個無效突變體以及野生型進行分子動力學模擬，野生型命名為Wild。模擬結果見表8所示。

表8 檢驗樣本模擬的平均能量Table 8 Average energy data simulated-test samples

表8下半部分第一列變化趨勢為有效突變體Q206C及N218S的能量變化結果，第二列為無效突變體P239G的結果。從數據可以看出，Q206C和N218S這兩個突變體的特征有效參數的取值滿足有效突變條件，并且能量變化的數值也處于上文中所提到的范圍之間，可以判斷Q206C和N218S為有效突變;而P239G的能量變化趨勢正好與之相反，為無效突變。

4.2 討 論

本文以枯草桿菌蛋白酶BPN＇為研究對象，利用4組不同條件分子動力學模擬結果，對其及其嗜熱突變體的能量變化趨勢進行對比分析，計算并提取了6個有效參數，并結合相關性分析結果，確定了4個特征有效參數，建立了判定枯草桿菌蛋白酶BPN＇嗜熱性突變效果的理論方法。研究發現，不同的模擬溫度與時間對突變前后各個能量的變化趨勢并沒有影響。而且在較短的模擬時間條件下，即模擬沒有達到平衡的狀態下，有效參數及特征有效參數具有相同的變化趨勢。本文提出的對枯草桿菌蛋白酶嗜熱效果改造的判定方法非常簡單有效，這將為以后篩選有效的突變體提供捷徑。

利用短時間(時間小于等于0.2 ns)分子動力學模擬結果提取有效參數，在P239位點對應的兩個突變體P239R和P239G上均出現了ΔVDW取值不同于正常ΔVDW取值范圍的離群值，具體結果見表2、4、5、及表 8。其中 P239R 為有效突變，對應ΔVDW為正值;P239G為無效突變，對應ΔVDW為負值，盡管ΔVDW的變化趨勢是對的，但P239R和P239G對應的ΔVDW明顯超出ΔVDW的取值范圍。這可能與脯氨酸(Pro)特殊的性質有關。由于脯氨酸是非極性氨基酸，而精氨酸(Arg)是極性帶正電的氨基酸，因而引入帶正電的Arg可以在增加蛋白的穩定性的同時使得分子極性大大增強，導致P239R的范德華能較其他幾個能量呈現出更大的增長，造成極端數據的出現。而甘氨酸(Gly)是非極性不帶電荷氨基酸，在P239G處為何也會出現極端數據，需要更多的實驗來進行統計與驗證。

此外，本文選取的試驗樣本僅為枯草桿菌蛋白酶，對其他蛋白酶是否具有普適性還需進一步研究與探討。

References)

［1］ NASCIMENTO W C A，MARTINS M L L.Production and properties of an extracellular protease from thermophilic Bacillussp ［J］. Brazilian Journalof Microbiology，2004，35(1-2):91-96.

［2］ ARGOS P，ROSSMAN M.G，GRAU U.M，ZUBER H.Thermal stability and protein structure ［J］.Biochemistry，1979，18(25):5698-5703.

［3］ ARNOLD F H，GIVER L，GERSHENSON A，ZHAO H.Directed evolution ofmesophilic enzymesinto their thermophilic counterparts ［J］.Ann N Y Acad Sci，1999，870:400-403.

［4］ LEHMANN M，LOCH C，MIDDENDORF A，et al.The consensus conceptforthermostability engineering of proteins:further proof of concept［J］. Protein Engineering，2002，15(5):403-411.

［5］ SEELIGER D，GROOT B L.Proteinthermostability calculations using alchemical free energy simulations［J］.Biophysical Journal，2010，98(10):2309-2316.

［6］ 田健，王平.理性設計提高蛋白質熱穩定性的研究進展［J］.生物技術進展，2012，4(2):233-239.TIAN Jian，WANG Ping.Recent advances in the rational design to improve the proteinthermostability［J］.Current Biotechnology，2012，4(2):233-239.

［7］ GROMIHA M M，UEDAIRA H，AN J.ProTherm:Thermodynamic Database for Proteins and Mutants:developments in version 3.0［J］.Nucleic Acids Res.，2002，30(1):301-302.

［8］ GRIBENKO A V，PATEL M M，LIU J，et al.Rationalstabilization of enzymes by computational redesign of surface charge-charge interactions［J］.Proc.Natl.Acad.Sci.，2009，106(8):2601-2606.

［9］ JOO J C，PACK S P，KIM Y H，et al.Thermostabilization of bacillus circulans xylanase:Computational optimization of unstable residues based on thermal fluctuation analysis［J］.Journal of Biotechnology，2011，151(1):56-65.

［10］ KORKEGIAN A，BLACK M.E，BAKER D.Computational thermostabilization of an enzyme［J］.Science，2005，308(5723):857-860.

［11］ SARABOJI K，GROMIHA M.Average assignment method for predicting the stability of protein mutants［J］.Biopolymers，2006，82(1):80-92.

［12］ CAPRIOTTI E，FARISELLI P.A neural-network-based method for predicting proteinstability changes upon single point mutations［J］.Bioinformatics，2004，20(Suppl 1):i63-68.

［13］畢汝昌，儲乃明.枯草桿菌蛋白酶與蛋白質工程［J］.生物化學與生物物理進展，1991，18(5):329-334.BI Ruchang，CHU Naiming.Subtilisin and protein engineering［J］.Progress in Biochemistry and Biophysics，1991，18(5):329-334.

［14］王凡強，馬美榮，王正祥，等.枯草桿菌蛋白酶基因工程的研究進展［J］.生物工程進展，2000，20(2):41-44.WANG Fanqiang，MA Meirong，WANG Zhengxiang，et al.The research progress of Subtilisin gene engineering［J］.Progress in Biotechnology，2000，20(2):41-44.

［15］ MCKENNEY J M，KOREN M J，KEREIAKES D J.Safety and efficacy of a monoclonal antibody to proprotein convertase subtilisin/kexin type 9 serine protease，SAR236553/REGN727，in patients with primary hypercholesterolemia receiving ongoing stable atorvastatin therapy［J］. Journalofthe American College of Cardiology，2012，59(25):2344-2353.

［16］ GUMBINER B，CHANDRASEKHAR U，JOH T.The effects of multiple dose administration of RN316(PF-04950615)，a humanized IgG2a monoclonal antibody bindingproprotein convertase subtilisin kexin Type 9，in hypercholesterolemic subjects［J］.Circulation，2012，126(suppl):A13524-A13524.

［17］ KIMBER I，BASKETTER D A.Categorisation of protein respiratory allergens:The case ofSubtilisin［J］.Regulatory Toxicology and Pharmacology，2014，68(3):488-492.

［18］ZHAO H M，ARNOLD F H.Directed evolution converts subtilisin E into a functional equivalent of thermitase［J］.Protein Engineering，1999，12(1):47-53.

［19］ PANTOLIANO M W，WHITLOW M，WOOD J F，et al.Large increases in general stability for subtilisin BPN＇through incrementalchangesin the free energy of unfolding［J］.Biochemistry，1989，28(18):7205-213.

［20］ S?TTLER A，KANKA S，MAURER K，et al.Thermostable variants of subtilisin selected by temperature-gradient gel electrophoresis［J］.ELECTROPHORESIS，1996，17(4):784-92.

［21］CUNNINGHAM B C，WELLS J A.Improvement in the alkaline stability of subtilisin using an efficient random mutagenesisand screening procedure［J］. Protein Engineering，1987，1(4):319-325.

［22］ TAKAGI H，MORINAGA Y，IKEMURA H，et al.The Role of Pro-239 in the Catalysis and Heat Stability of Subtilisin E［J］.Journal of Biochemistry，1989，105(6):953-956.

［23］ RADESTOCK S，GOHLKE H.Protein rigidity andthermophilic adaptation［J］.Proteins:Structure，Function，and Bioinformatics，2011，79(4):1089-1108.

［24］CHAN C H，WILBANKS C C，MAKHATADZE G I，et al.Electrostatic contribution of surface charge residues to the stability of a thermophilic protein:Benchmarking experimental and predicted pKa values［J］.PloS One，2012，7(1):e30296.