有時間窗的車輛路徑問題改進蟻群算法研究

董 攀，陳 陽（長沙理工大學 經濟與管理學院，湖南 長沙 401114）

0 引言

車輛路徑問題（Vehicle Routing Problem,VRP）屬于組合優化問題，其理論涉及到運籌學、管理學、交通運輸、計算機應用等多個學科。VRP問題中加入節點可訪問的時間窗約束即成為有時間窗車輛路徑問題（Vehicle Routing Problem with Time Windows,VRPTW）。由于現實生活中很多問題可以歸結為VRPTW，因此VRPTW的研究受到學術界的廣泛重視。

VRPTW已被證明為NP-hard問題，這意味著當節點規模較大時，很難在多項式時間內得到問題的精確解，因此啟發式算法因其快速高效構建可行解的優點成為人們的首選。Ombuki Beatrice等[1]利用遺傳算法、Tavakkoli-Moghaddam等[2]利用模擬退火算法來求解VRPTW問題，但二者都存在收斂速度慢的問題；張炯和郎茂祥[3]使用的禁忌算法、馬炫等[4]使用的粒子群算法則容易陷入局部最優解。為解決這些問題，蟻群算法的魯棒性和構造簡單使得其經常被用于與其他算法構成組合優化算法。但無論是殷志鋒和張巖松[5]提出的基于進化規劃和最大-最小蟻群算法相融合的混合蟻群算法，還是范小寧等[6]采用遺傳算法和蟻群算法的結合，以及Zhang Xiaoxia[7]將蟻群算法和禁忌搜索結合等都只是將蟻群算法作為構造可行解的方法，并大量使用局部搜索優化算法，而缺少對蟻群算法本身的改進。

本文對Thomas Thutzle和Holger Hoos提出的最大最小蟻群系統（MAX-MIN ant colony system）在轉移概率矩陣計算、信息素更新等關鍵因素上進行改進，以提高其全局優化能力。為更好地說明本改進算法的優越性，在原始MMAS算法和本文算法測試Solomon標準數據集時均不使用局部優化算法。

1 有時間窗車輛路徑問題的定義

VRPTW的一般定義如下：從某一物流中心用多臺配送車輛從多個客戶取貨，每個客戶的位置和需求量和需求時間一定，每個客戶只能由一臺車輛服務一次，要求合理安排車輛配送路線，使目標函數得到最優，即在不違背約束條件下所用車輛數最少和行走路線長度最短。本文將最小化車輛數量作為第一目標，最小化車輛行駛路線長度作為第二目標。

2 最大最小蟻群算法及其在有時間窗車輛路徑問題中的應用

MMAS對AS的關鍵改進在于將路徑上的信息素濃度限定 ［τmin,τmax］之間，這較好地避免了搜索陷入局部最優解。因為在搜索過程中，隨著信息素的揮發和累積，某些路徑上的信息素濃度會遠遠高于其他路徑，從而導致搜索過早停滯。

2.1 狀態轉移概率。螞蟻在選擇下一個節點時，在滿足容量約束和時間窗約束下，需要考慮如下三個因素：①通往下個節點的路徑長度以及路徑上的信息素濃度[8]。②時間窗因素的擇優性[8]，由下個客戶j的時間窗寬度和所在客戶i到達下個客戶j的時間等因素決定。這種擇優性的優先原則為，需等待時間較短優先原則和時間窗較小優先原則。③基于Wissner-Gross,A.D.[9]的事物傾向于向自由度大的方向進化的理論，潛在下一可行節點數多的節點有優先權。

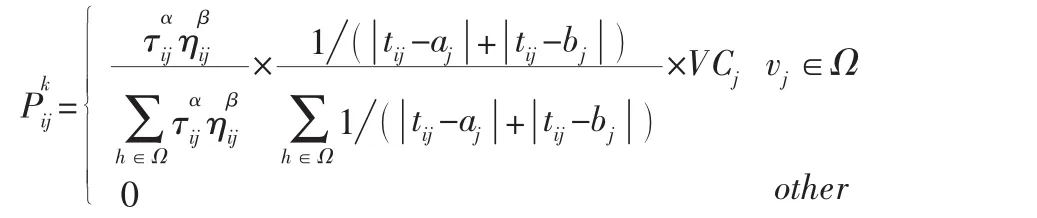
其中，Ω=｛vj|vj為可被訪問的客戶 ｝，v0為配送中心。為客戶j的時間窗；tij為從客戶i到達客戶j的時間（等于開始為客戶i服務的時刻+客戶i所需服務時間+從客戶i到客戶j的時間）；VCij為客戶j的下一潛在可被訪問客戶數，由所有滿足LTi+Si+Lij≤LTj的客戶組成。τij為vi和vj之間路徑上的信息素；ηij為路徑可見性，這里ηij=1 dij，dij為客戶i與j之間路徑長度。α和β為路徑上信息素與路徑可見性的權重。

2.2 動態啟發式信息更新。因為VRPTW問題的第一目標值為最小化車輛數量，因此為強化改進蟻群算法構建最小化車輛數量路徑的性能，本文對上面狀態轉移概率中的信息素和路徑長度啟發式做如下改變：

式中antTypei為精英螞蟻策略中進行信息素更新的螞蟻類型。Rand（）為隨機值。t為信息素更新隨機因子。因為ηij為路徑值啟發式信息，因此將其以t的概率增加螞蟻構建更優的車輛數量的解集合。

2.3 精英螞蟻策略。鑒于MMAS有搜索時間過長問題，現有文獻通常采用兩種方式最鄰近城市和精英螞蟻，這兩種方式并不能改善最終解，只是起到加快搜索的作用。本文將精英螞蟻策略引入到改進蟻群算法。

現有文獻傾向于使用固定數量或某種逐步縮小數量的辦法來使用精英螞蟻，這兩種方式忽略了蟻群算法的易于收斂于次優解的特性。在蟻群搜索過程中，由于信息素的累積作用，構建的路徑中次優解往往大量出現。為此本文采用動態固定數量精英螞蟻，即螞蟻數量固定，但不是單純的迭代最優的前幾個，而是選擇固定數量的目標值各不相同的前幾個螞蟻進行迭代，這是通過將一次迭代中構建的目標值排序，將重復值剔除后選擇迭代最優的幾個實現的。本文通過實驗發現，對于具有n=100個客戶的VRPTW，精英螞蟻數選擇5個，最多能節約三分之一的有效迭代次數，即得到全局最優解的最大迭代。

3 試驗結果及分析

將改進的蟻群算法應用于Solomon[10]標準數據集，這些實例共56個。每個問題中包含100個客戶點。程序用JAVA語言編寫，并在eclipse下編譯運行。

3.1 參數設定。通過逐步改進法得到參數如下：螞蟻數M=100，迭代次數N=1 500，信息素權重α=1.18；路徑可見性權重β=2.26；信息素揮發率ρ=0.0118；PBest=0.058；信息素更新隨機因子t=0.5。

3.2 結果及分析。本文對Solomon標準數據集中的所有實例均運行8次，計算結果的最優值和平均值，并與原始MMAS方法以及目前已知最優解進行了比較。結果如表1～6所示。

從以上結果分析中可以得出：（1）MMAS原算法的計算性能已經非常好。相比于引進了時間窗啟發式信息的改進算法，沒有使用時間窗啟發式信息并沒有造成性能上非常大的損失，其原因首先是因為使用過的參數是事先經過了優化的；其次的一個重要原因是最早開始服務時間窗約束實質上沒有起作用。因為中間的等待時間按照與距離同單位換算原則，應該加入到路徑長度中，但事實上即便是目前學術界取得的最優解中公布了路徑節點排列清單的也沒有將其考慮進去。（2）改進的蟻群算法明顯優于原始MMAS算法。與原始MMAS方法的比較可知，改進的蟻群算法在解決R類和RC類問題上較好，但在C類問題上稍弱。

4 結束語

本文研究了在不使用局部搜索算法的情況下，通過改進螞蟻選擇路徑的狀態轉移概率和信息素更新方式，很好地將MMAS運用于解決VRPTW問題。通過使用Solomon標準數據集，驗證了改進的蟻群算法的有效性。

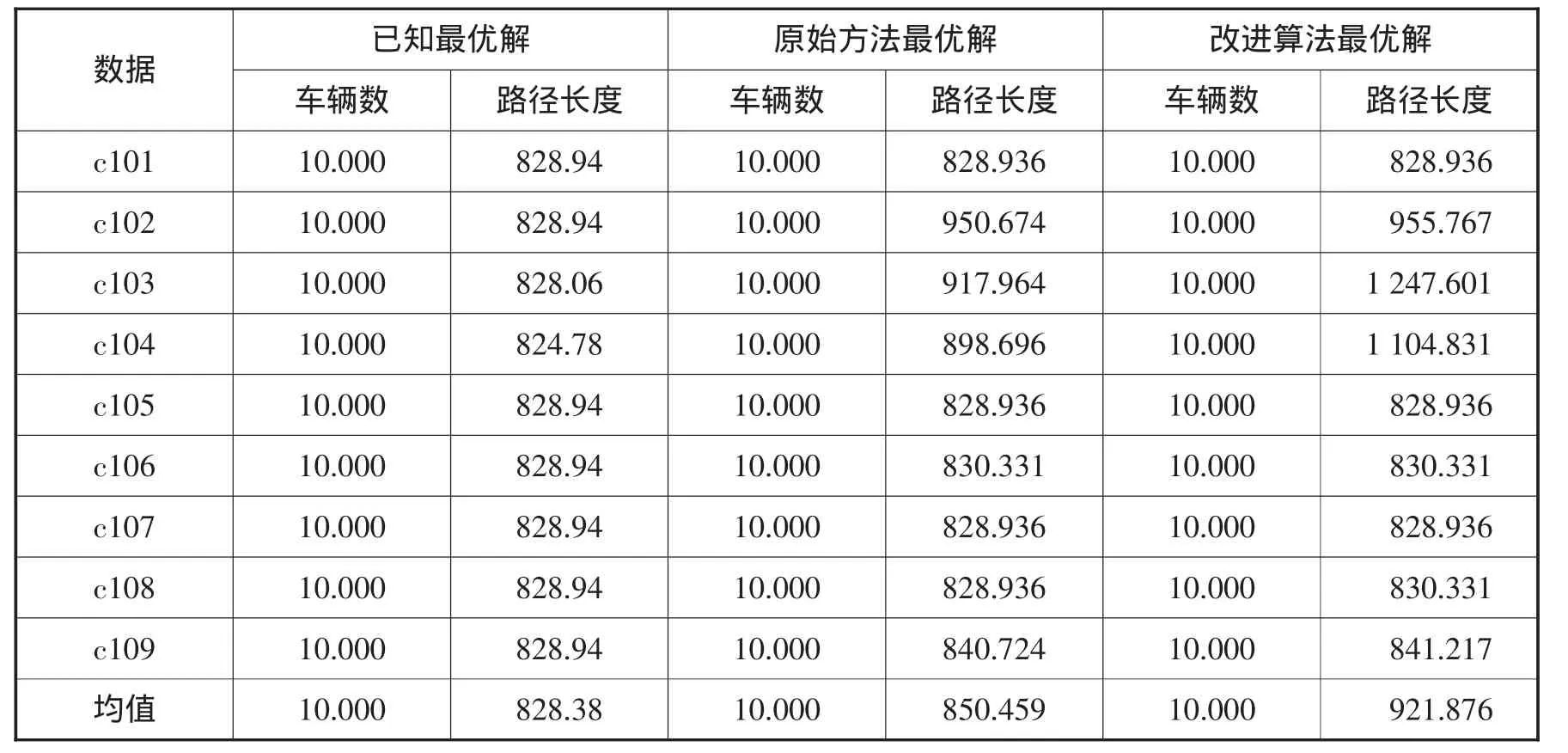
表1 C1類數據集結果比較

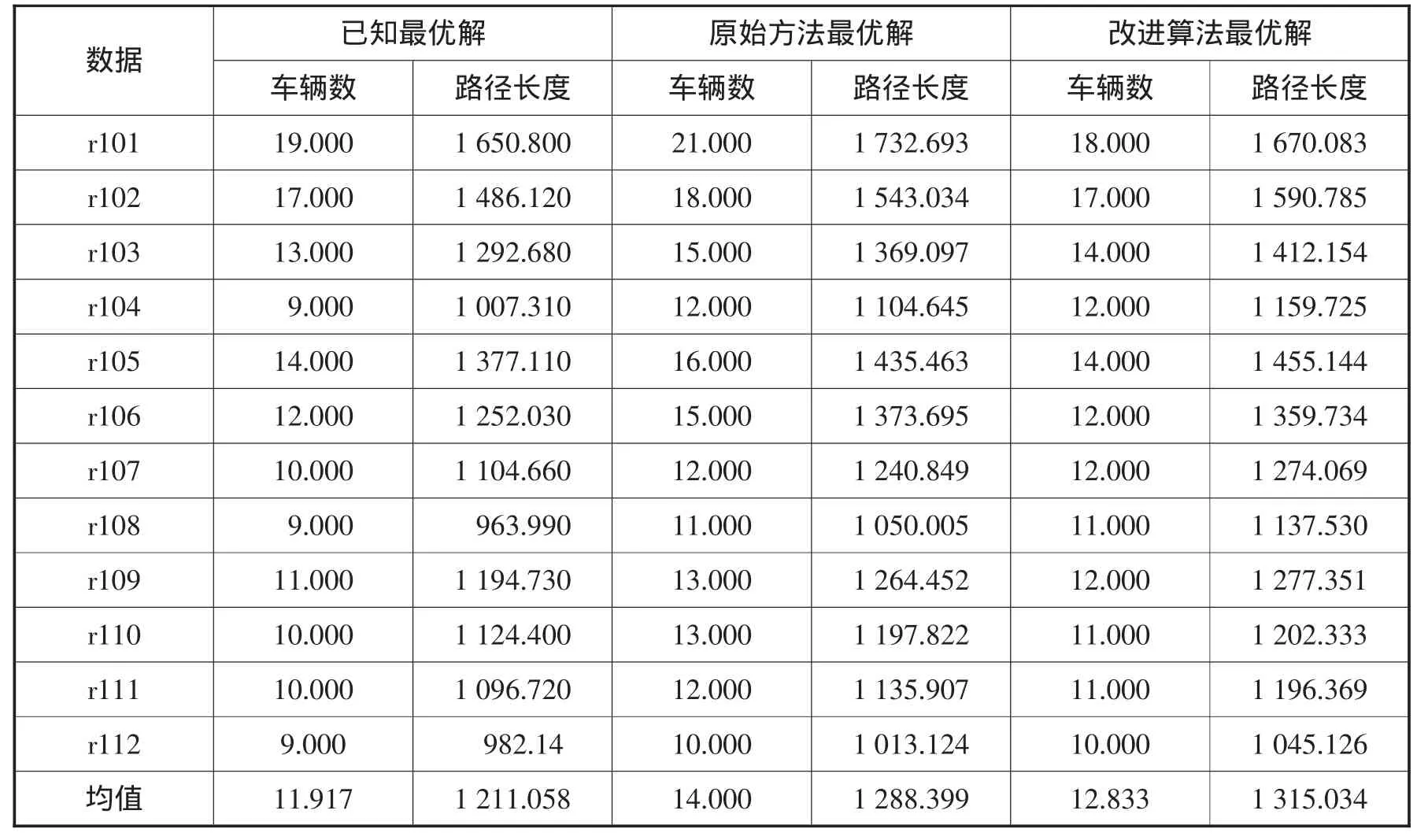
表2 R1類數據集結果比較

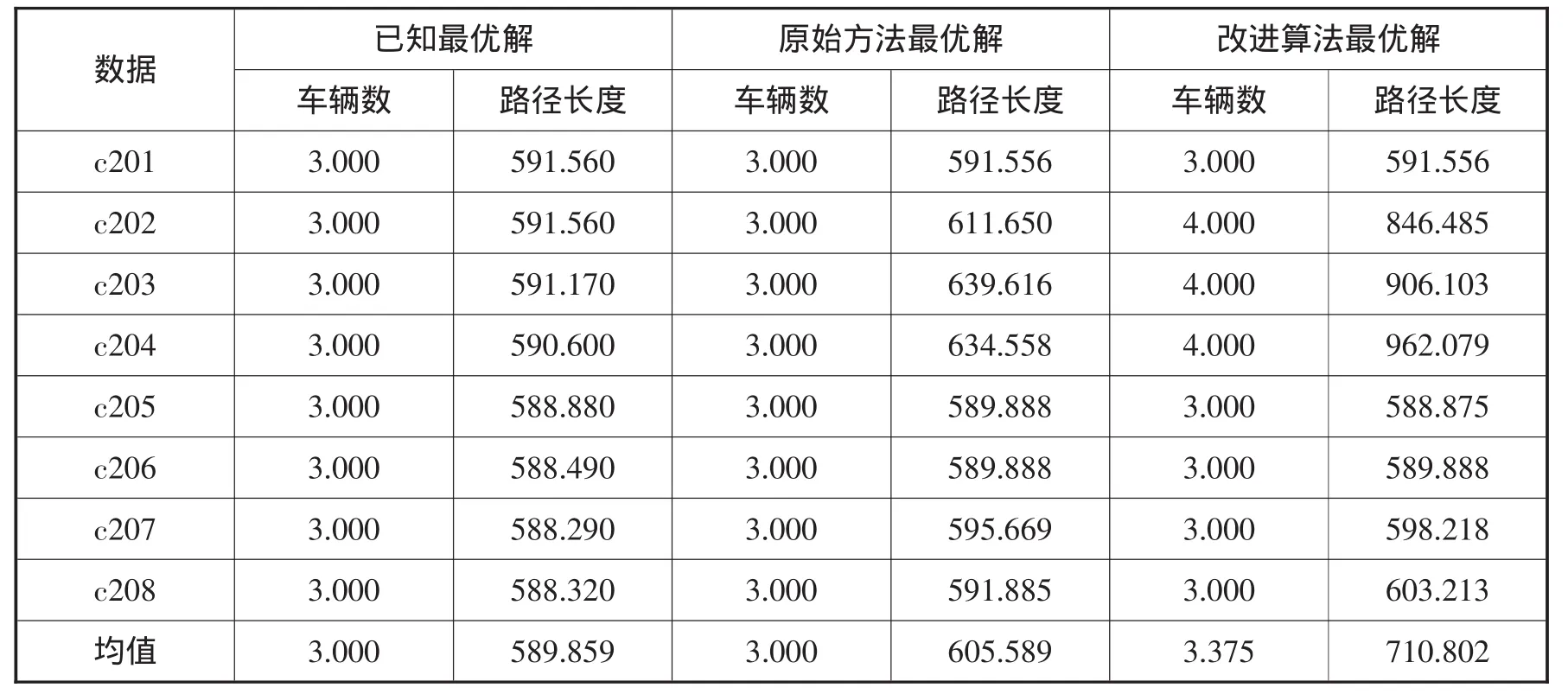
表3 C2類數據集結果比較

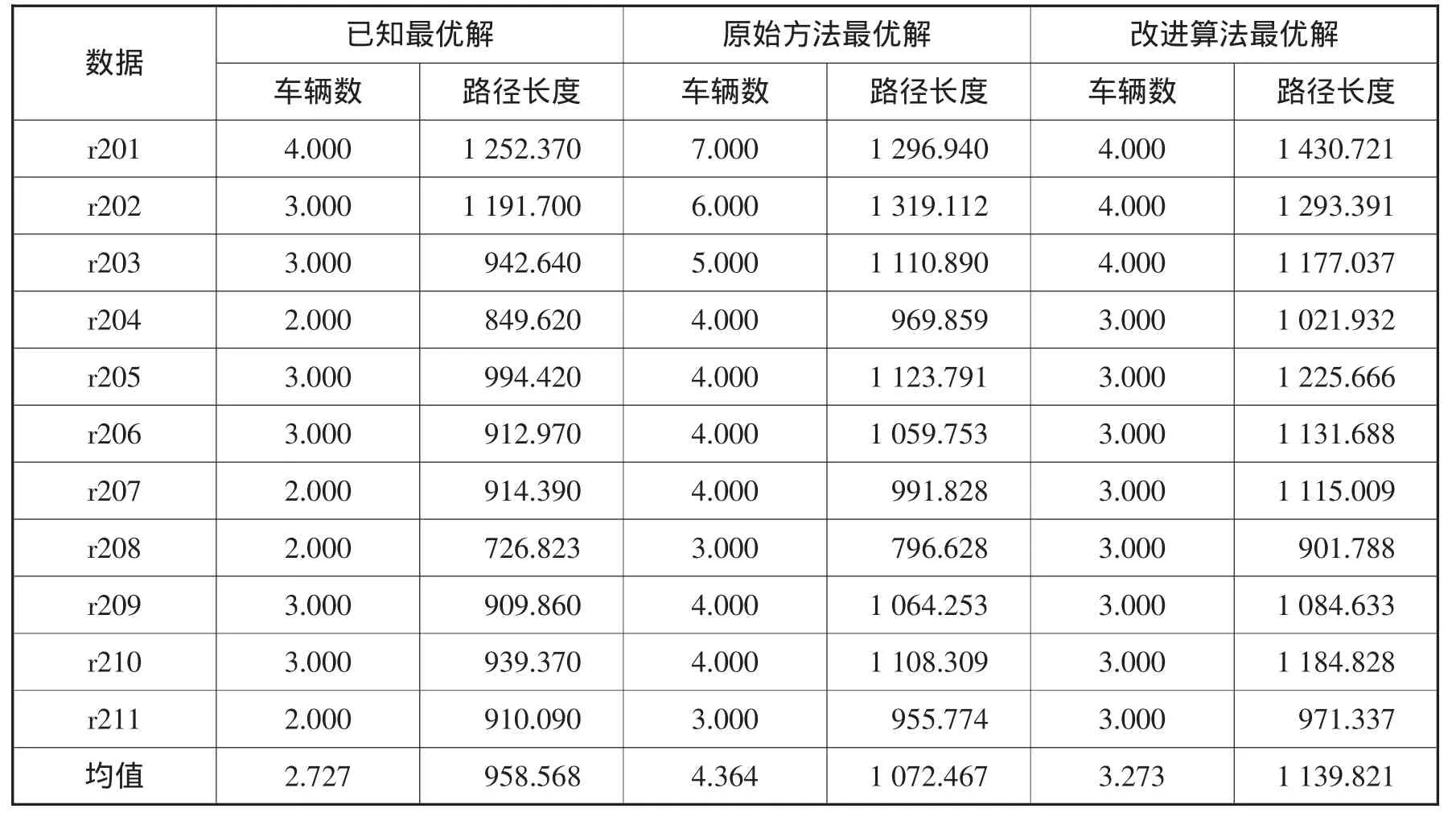
表4 R2類數據集結果比較

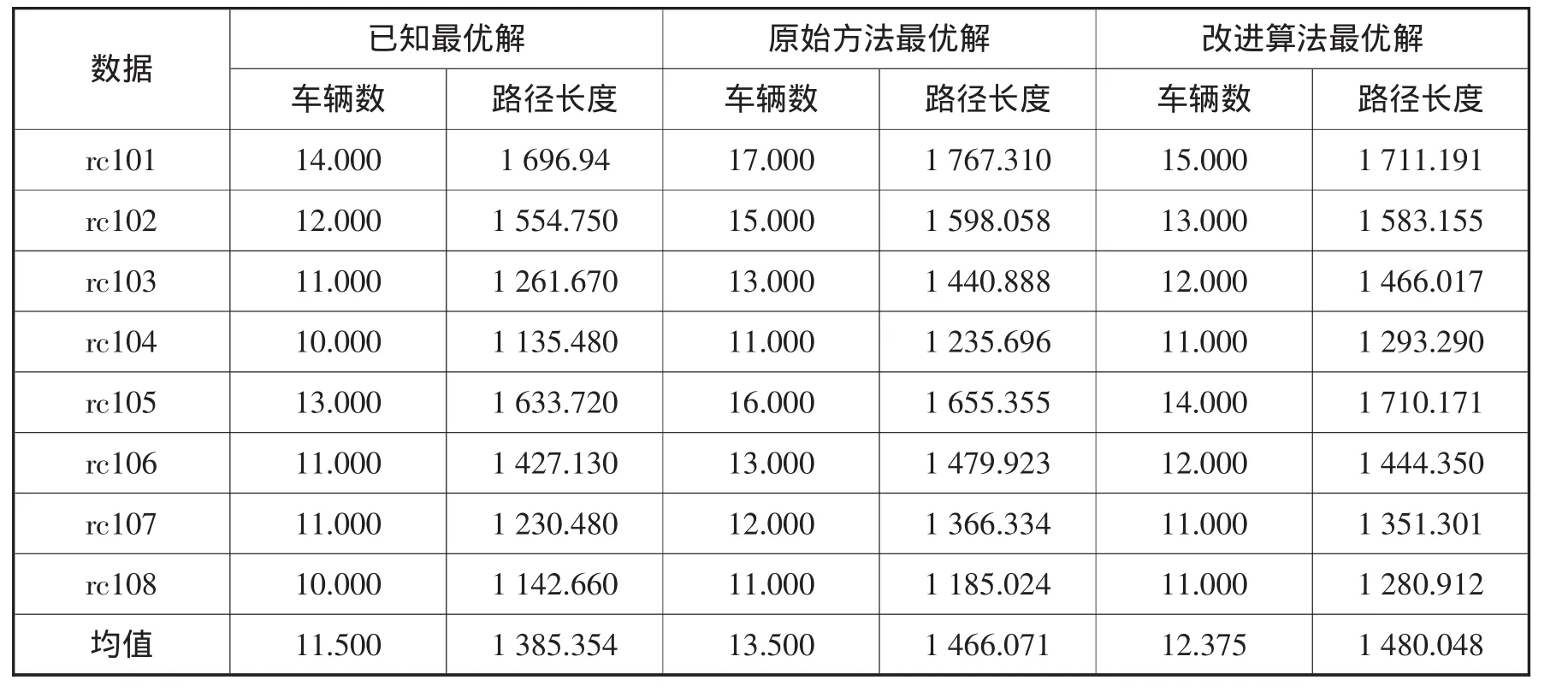
表5 RC1類數據集結果比較

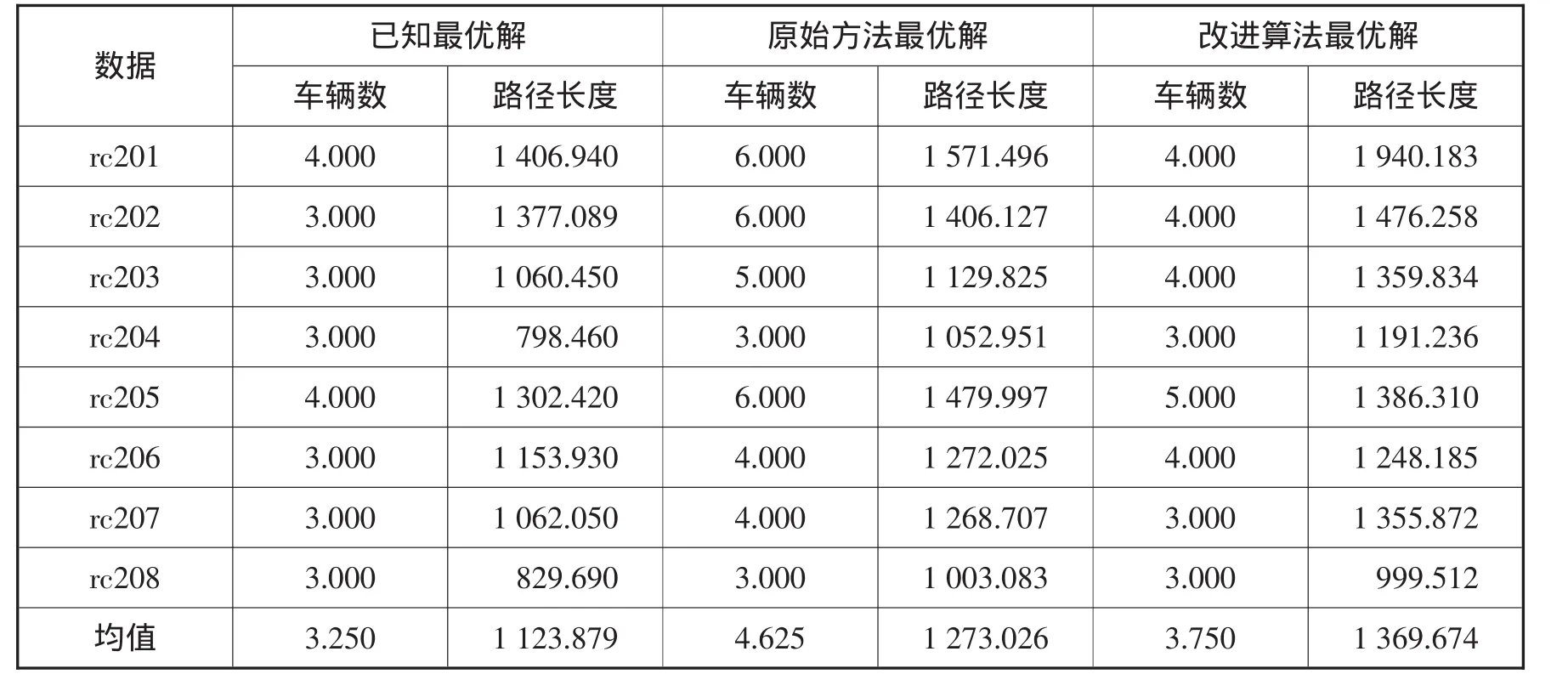
表6 RC2類數據集結果比較

[1] Franklin,O.B.B..Multi－Objective Genetic Algorithms for Vehicle Routing Problem with Time Windows[J].Applied Intelligence,2006,24:17－30.

[2] Tavakkoli－Moghaddam R.,Gazanfari M.,Alinaghian M,et al.A new mathematical model for a competitive vehicle routing problem with time windows solved by simulated annealing[J].Journal of Manufacturing Systems,2011,30:83－92.

[3] 張炯，郎茂祥.有時間窗配送車輛調度問題的禁忌搜索算法[J].北方交通大學學報，2004(2):103－107.

[4] 馬炫，彭破，劉慶.求解帶時間窗車輛路徑問題的改進粒子群算法[J].計算機工程與應用，2009,45(27):200－202.

[5] 殷志鋒，張巖松.帶時間窗車輛路徑問題的混合蟻群算法[J].許昌學院學報，2008,27(2):88－90.

[6] 范小寧，徐格寧，楊瑞剛.車輛配送路徑優化的新型蟻群算法[J].計算機工程與應用，2011,47(26):232－234.

[7] Yu B.,Yang Z.B..A hybrid algorithm for vehicle routing problem with time windows[J].Expert Systems with Applications,2011,38:435－441.

[8] 萬旭，林建良，楊曉偉.改進的最大最小螞蟻算法在有時間窗車輛路徑問題中的應用[J].計算機集成制造系統，2005,4(11):572－576.

[9] Wissner－Gross,A.D.,C.E.Freer.Causal Entropic Forces[J].Physical Review Letters,2013,110:16.

[10] Solomon M M.Algorithms for the vehicle routing and scheduling problems with time window constraints[J].Operations research,1987,35(2):254-265.