基于Logistic函數的貝葉斯概率矩陣分解算法
方耀寧郭云飛 蘭巨龍
(國家數字交換系統工程技術研究中心 鄭州 450002)
1 引言
當前,推薦系統(Recommender Systems, RS)是電子商務領域的研究熱點之一。與基于內容的(Content-based)推薦算法相比,協同過濾(Collaborative Filtering, CF)推薦算法無須對內容進行解析,只利用歷史行為信息便可以進行個性化推薦,在過去十年中取得了豐富的研究成果。其中,基于矩陣分解(Matrix Factorization, MF)的潛在因子模型(latent factor model)在預測準確性和穩定性上得到了最為廣泛的認可[1]。
核矩陣分解算法(kernelized matrix factorization)雖然能夠表征潛在因子間的非線性聯系,但是計算量較大并不實用[8,9]。此外,項目間的隱含關系,用戶的社交信息,上下文也可以用來提高矩陣分解算法的性能[10,11]。最近,Mackey等人[12]提出“分而治之”的思想,把原始矩陣拆分成多個小矩陣分別進行分解。與之類似,文獻[13]假設原始矩陣是局部低秩的,把原始矩陣分解為多個低秩矩陣,然后再進行分解。文獻[14]和文獻[15]在 Netflix和MovieLens數據集合上對主流的推薦算法進行了較為詳細的對比分析。
本文利用 Logistic函數來表征潛在因子間的非線性關系,在不增加計算復雜度的前提下,建立了L-BPMF(Logistic Bayesian Probabilistic Matrix Factorization)模型,并使用馬爾科夫鏈蒙特卡羅方法訓練L-BPMF模型。在兩種真實數據集合上的實驗結果表明,L-BPMF比主流推薦算法的預測準確性都要好,能夠明顯緩解數據稀疏性問題[15]。
2 貝葉斯概率矩陣分解
概率矩陣分解(Probabilistic Matrix Factorization, PMF)假設用戶和項目的特征向量矩陣都服從高斯分布,不同用戶、項目的概率分布相互獨立[6]。

進而,把用戶對項目的評分變成一個概率問題:

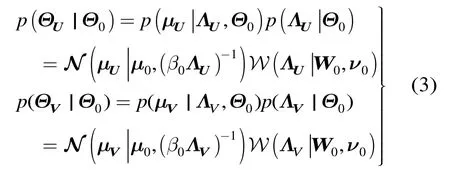

圖1 Bayesian PMF模型[7]
BPMF模型一般用馬爾科夫鏈蒙特卡羅方法進行訓練,雖然預測誤差較小,但仍然是一種線性模型。線性模型不能反映用戶特征U和項目特征V之間的非線性關系,這一定程度上限制 BPMF的性能,特別是在數據稀疏條件下提取潛在信息的能力。
3 基于Logistic函數的BPMF算法
3.1 Logistic BPMF模型
Logistic函數是機器學習領域中常用的一種 S型函數,定義域為,值域為。Logistic函數在定義域內單調連續,呈現出先緩慢增長,然后加速增長,最后逐漸穩定的趨勢,能夠較好反映生物種群發展、神經元非線性感知、人類認知學習過程等[16]。受數理情感學中情感強度第一定律啟發,本文用Logistic函數的橫軸表示用戶感知到的“刺激”,縱軸表示用戶評分:用戶受到的“刺激”為正,則評分大于評分均值;“刺激”越強烈,評分越高;原點附近評分隨“刺激”變化較快,屬于敏感區域;偏離原點處評分隨“刺激”變化緩慢,屬于麻木區域[16,17]。
Logistic BPMF模型如圖2所示,其核心改進是假設用戶 i對項目 j的評分 Rij服從均值為方差為的高斯分布,即
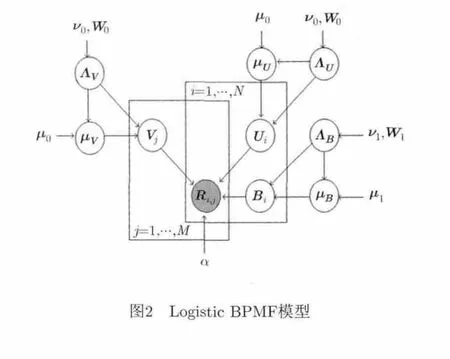
圖2 Logistic BPMF模型



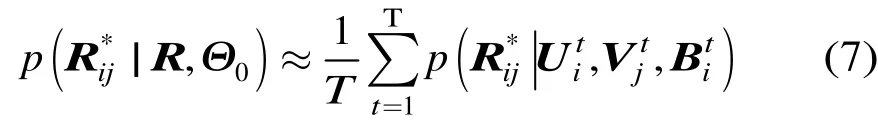
3.2貝葉斯推斷與吉布斯抽樣
. 貝葉斯推斷(Bayesian inference)是將先驗的思想和樣本數據相結合,得到后驗分布,然后根據后驗分布進行統計推斷。貝葉斯推斷的精度受到樣本數量和先驗分布準確性的影響。在先驗分布一定的情況下,樣本數量越大則推斷精度越高。本文在訓練Logistic BPMF的過程中,使用吉布斯抽樣進行貝葉斯推斷。吉布斯抽樣(Gibbs sampling)是一種典型的 MCMC方法,適用于聯合概率未知,但條件概率容易獲取的情況。首先利用條件概率構造平穩分布為所求聯合概率的馬爾科夫鏈,然后進行T次抽樣,此時的樣本可以近似認為是來自聯合概率的抽樣,最后利用式(7)進行評分預測。
使用吉布斯抽樣方法進行貝葉斯推斷,條件后驗概率必須要有顯示解,即明確的新樣本產生規則。L-BPMF模型中,在已知其它參數的條件下,Ui的條件后驗概率為

為了簡化式(9)的形式,本文對Logistic函數進行麥克勞林展開, 于是

根據共軛先驗分布理論:若方差已知,高斯分布均值的共軛先驗分布是高斯分布[7],利用配湊平方和的方法可以得到


已知樣本B,超參數BΘ的條件后驗概率可以利用高斯-威沙特分布的性質得到。

3.3 算法復雜度分析
4 實驗設計及結果分析
4.1 數據集合及評價標準
為了測試L-BPMF算法的有效性,本文采用推薦系統常用的兩種數據集合:Netflix和MovieLens。Netflix數據集合是Netflix Prize比賽中使用的標準測試數據集,本文從中隨機抽取了包含8662名用戶對 3000部視頻的約5310×條評分信息(評分密度為1.1%)作為測試集合。MovieLens數據集合由GroupLens提供,MovieLens 1M數據集包含了6039名用戶對 3883部電影的610條評分信息(評分密度為4.3%);MovieLens 100K數據集包含了943名用戶對 1682部電影的條評分信息(評分密度為6.3%)。
文獻[18]全面總結了推薦系統領域各種不同的評價標準,文中采用檢驗推薦算法最常用的預測誤差MAE和RMSE 作為評價依據,預測誤差越小則表示算法性能越好。其中是測試集合,是testS 中的元素個數。

4.2 實驗設計及結果
本文在上述兩種數據集合上,以 MAE和RMSE為評價標準,設計了3組實驗從不同方面對L-BPMF的性能進行測試,每組結果都是10次實驗結果的平均值。
A組實驗在Netflix和MovieLens 1M數據集合上,隨機選取不同比例的訓練集合,對L-BPMF和經典 BPMF進行了對比(特征維度 10d= ),使用RSVD(學習率lr 0.005= ,正則化因子的預測誤差作為參考。實驗結果如圖3,圖4所示。在Netflix數據集合上,L-BPMF比BPMF的預測誤差小約1%,而且在訓練比例較低時優勢更明顯,在訓練比例為 20%時能夠降低約 1.5%;在MovieLens 1M數據集合,L-BPMF比RSVD的預測誤差小1%~2%,L-BPMF和BPMF預測準確性基本一致,在訓練比例較低時L-BPMF略好一點。分析發現,Netflix數據集合的評分密度只有1.1%,而MovieLens 1 M的評分密度為4.3%。一種可能的解釋是,評分密度較大時L-BPMF與BPMF的性能基本一致,評分較稀疏時L-BPMF比BPMF的預測誤差更小。
為了驗證上述結論,利用MovieLens 100K數據集合產生評分密度<1.5%的訓練環境,進行B組測試。實際應用中的評分密度都在1%以下,稀疏條件下的實驗更能反映算法提取潛在信息的能力。從圖5中可以看出,L-BPMF的RMSE預測誤差比BPMF低約2%,在最壞的情況下也能夠降低約1%的預測誤差。這說明L-BPMF提取潛在信息的能力要大于BPMF,能夠有效緩解數據稀疏性問題。
C組以MAE為指標對比了L-BPMF和其它主流推薦算法(RSVD, SVD++, KNN, Slope One[19]),實驗結果如圖6所示[20]。其中,RSVD的參數與A組實驗相同;SVD++算法中學習率lr 0.005= ,正則化因子; RSVD, SVD++的特征空間維度d為20, L-BPMF算法的特征維度為10。都只記錄了訓練過程中的最優值,并未記錄過擬合現象。KNN算法中以皮爾森相似度公式計算相似性,選擇與目標用戶最相似的20個用戶作為鄰居進行預測。一般來說,KNN算法中鄰居數目小于20時預測準確性會明顯下降[14]。

圖3 Netflix上L-BPMF與BPMF的對比

圖4 MovieLens 1M上L-BPMF 與BPMF的對比

圖5 稀疏條件下L-BPMF 與BPMF的對比
從圖6中可以看出,L-BPMF和SVD++是預測誤差最小的兩種算法,L-BPMF的MAE誤差比RSVD低約0.5%~1.5%。因為L-BPMF特征維度為10, SVD++的特征維度為20,而且L-BPMF的性能略高于SVD++,這說明L-BPMF能夠用較小的特征維度d獲得更高的預測準確性。

圖6 主流推薦算法的MAE預測誤差比較
5 結束語
本文針對經典貝葉斯概率矩陣分解模型不能表征潛在因子間非線性關系的問題,提出一種利用Logistic函數的L-BPMF模型,并使用MCMC方法對模型進行訓練。在兩種真實數據集合上的實驗表明,L-BPMF能夠明顯提高預測準確性,用較小的特征維度獲得比RSVD和SVD++更好的性能。在稀疏條件下的測試結果表明,L-BPMF比BPMF提取信息的能力更強,能夠有效緩解數據稀疏性問題。
[1] Koren Y, Bell R, and Volinsky C. Matrix factorization techniques for recommender systems[J]. IEEE Computer,2009, 42(1): 30-37.
[2] Billsus D and Pazzani M J. Learning collaborativeGranada, 2012: 1134-1142.
[13] Lee J, Kim S, Lebanon G, et al.. Local low-rank matrix approximation[C]. Proceedings of the 30th International Conference on Machine Learning (ICML-13), Atlanta, 2013:82-90.
[14] Cacheda F, Carneiro V, Fernandez D, et al.. Comparison of collaborative filtering algorithms: limitations of current techniques and proposals for scalable, high-performance recommender systems[J]. ACM Transactions on Web, 2011,5(2): 1-33.
[15] Lü Lin-yuan, Medo M, Yeung C H ,et al.. Recommender systems[J]. Physics Reports, 2012, 1(3): 159-172.
[16] Jordan M I. Why the logistic function? a tutorial discussion on probabilities and neural networks[J]. MIT Computational Cognitive Science Report , 1995, 9503: 1-13.
[17] 仇德輝. 數理情感學[M]. 長沙: 湖南人民出版社,2001:55-60.Qiu De-hui. Mathematical Emotions[M]. Changsha, Hunan People’s Publishing House, 2001: 55-60.
[18] 朱郁筱, 呂琳媛. 推薦系統評價指標綜述[J]. 電子科技大學學報, 2012, 41(2): 163-175.Zhu Yu-xiao and Lü Lin-yuan. Evaluation metrics for recommender systems[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(2): 163-175.
[19] Lemire D and Maclachlan A. Slope one predictors for online rating-based collaborative filtering[J]. Society for Industrial Mathematics, 2005, 5(1): 471-480.
[20] 方耀寧, 郭云飛, 丁雪濤, 等. 一種基于局部結構的改進奇異值分解推薦算法[J]. 電子與信息學報, 2013, 35(6): 1284-1289.Fang Yao-ning, Guo Yun-fei, Ding Xue-tao, et al.. An improved Singular Value Decomposition recommender algorithm based on local structures[J]. Journal of Electronic& Information Technology, 2013, 35(6): 1284-1289.

