采用諧波分析的直線度誤差信號提取

黃麗玲，李興旺，王宇，王煥玲，黃富貴

（華僑大學 機電及自動化學院，福建 廈門361021）

形位誤差測量的提取、濾波、擬合與評定是新一代GPS有關幾何量測量標準的重要環節，合理規范這些環節的要求無疑對形位誤差測量的操作具有重要的指導意義［1］.在國家標準GB／T 1958－2004《產品幾何量技術規范（GPS）形狀和位置公差 檢測規定》［2］以及ISO相關標準中，明確規定了提取方案的各種形式及其適用對象.對于提取點數，相關標準沒有做出明確的規定，只是建議提取點數應根據奈奎斯特采樣定理來確定［3－4］.久曾神煌［5］利用諧波分析法研究圓度誤差提取點數問題，得到圓度誤差提取點數與被測圓諧波最高次數和設計精度有關；費斌等［6］在奈奎斯特采樣定理的基礎上，提出了圓度誤差的自適應采樣法；趙前程等［7］提出二次判別法，對圓度誤差的測量點數進行合理性判別.此外，還有用智能搜索法、神經網絡法、曲線回歸法等方法研究形位誤差提取點數的問題［8－10］.他們的研究都未建立在以直線度誤差為例的非圓類形位誤差對象提取點數的確定準則上.諧波分析法又稱信號的頻域分析法，是一種利用變換域進行分析的方法［11］.現有研究已將諧波分析的方法應用于圓度、圓柱度等形位誤差項目中，但未見其在非周期的直線度誤差信號的測量提取問題中的應用.本文通過5組實驗，將諧波分析的方法應用于直線度誤差提取問題中.

1 直線度誤差信號的諧波分析

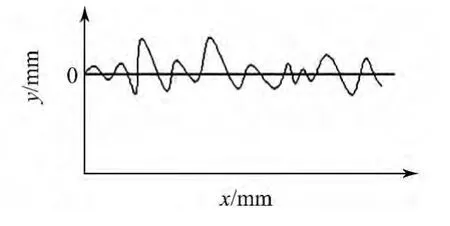
圖1 被測直線信號的示意圖Fig.1 Schematic diagram of the measured linear signal

對平面內直線度誤差的幾何要素線上部分點的坐標數據進行提取的操作，就是將被測直線（連續信號）進行離散化采樣的操作.被測直線信號是空域信號而非時域信號，如圖1所示.圖1中：提取方向x為自變量，反映被測直線的長度；誤差方向y為變量，反映被測直線的誤差.

設被測直線為y＝f（x），直線總長度為L，對該被測直線進行均勻布點提取，且在整段直線上的提取點數為m＋1個，則提取間距為ΔL＝L／m.另設提取直線上離散點的坐標數據為（xk，yk），k＝0，1，2，…，m.其中：xk＝x0＋k·ΔL，x0為被測直線起始坐標.被測直線度誤差信號為非周期的信號，無法直接采用周期信號諧波分析的方法.因此，采取周期延拓的方法，將其視為廣義的周期信號，將幾何要素線的總長L視為周期延拓后空域周期信號的主周期.與時域信號相對應，被測直線信號的波長成分對應于時域信號的頻譜成分，被測直線信號的提取間距對應于時域信號的采樣頻率.根據信號頻譜分析原理，被測直線信號可以分解成直流信號、基波波長的信號、二次諧波波長的信號，直至m次諧波波長的信號的疊加.其直流信號表達式為

其傅里葉系數為

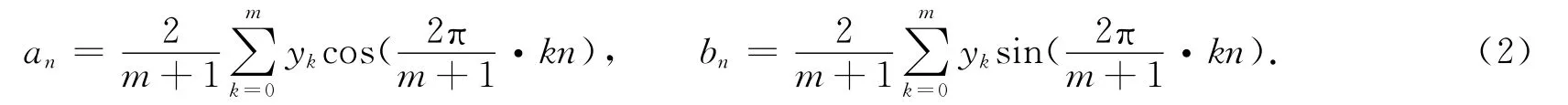
第n次諧波波長信號的綜合幅度為

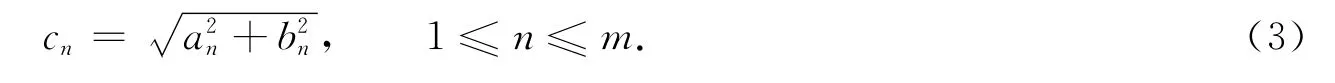
2 諧波分析實驗

采用測量坐標值檢測原則和布點提取方案，以Global Status 7.7.7活動橋式三坐標測量機為測量設備進行直線輪廓邊緣的坐標數據獲取.在室內溫度為25℃，空氣相對濕度為40%～60%條件下，對平面內的直線度誤差的幾何要素線進行測量［12］，被測對象的信息如表1所示.表1中：L為被測直線長度；m為測量點數.

表1 實驗對象信息Tab.1 Information of experimental objects

1）選取測頭并校準后，將擦洗干凈的被測對象放在Global Status 7.7.7型三坐標測量機工作臺上，手動建立零件坐標系.

2）在零件坐標系下初步確定被測對象的評定長度，設定采樣最大增量0.1mm，然后在DCC mode下采用均勻分布的自動掃描測量采集數據.

3）將上述掃描測量采集的數據導出，得到格式為TXT的文本文件.

4）將數據導入MATLAB軟件中進行數據處理與分析.

對5個零件的被測表面直線度誤差的幾何要素線作了不同點數的測量，得到所測點的坐標（xk，yk），k＝0，1，2，…，m.將數據導入MATLAB軟件中，并按照上述諧波分析的原理進行處理，得到直線度誤差諧波分析圖和數據點分布圖，分別如圖2，3所示.圖2，3中：A為幅值；n為諧波次數；e為誤差.

從圖2可知：零件1和零件4低頻段的諧波幅值較大，且逐漸變小，占了信號的主要部分；零件2基波幅值比其他階次諧波的幅值大得多，說明信號存在一個較大的確定性誤差成分；而零件3和零件5的諧波圖形呈現出雜亂無章的規律.部分信號經諧波分析后未能發現占主頻成分的諧波成分，又因信號中都含有隨機誤差信號成分的特征，而隨機誤差信號其最高頻率趨于無窮大.因此，通過此諧波分析的方法無法確定出被測直線信號最高次諧波波長.實驗結果表明：標準中直接依據奈奎斯特采樣定理來確定提取點數的方法是不可行的，但并不意味著上述諧波分析的方法和奈奎斯特采樣定理在提取點數準則確定中沒有任何其他的應用.

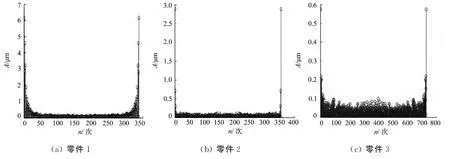
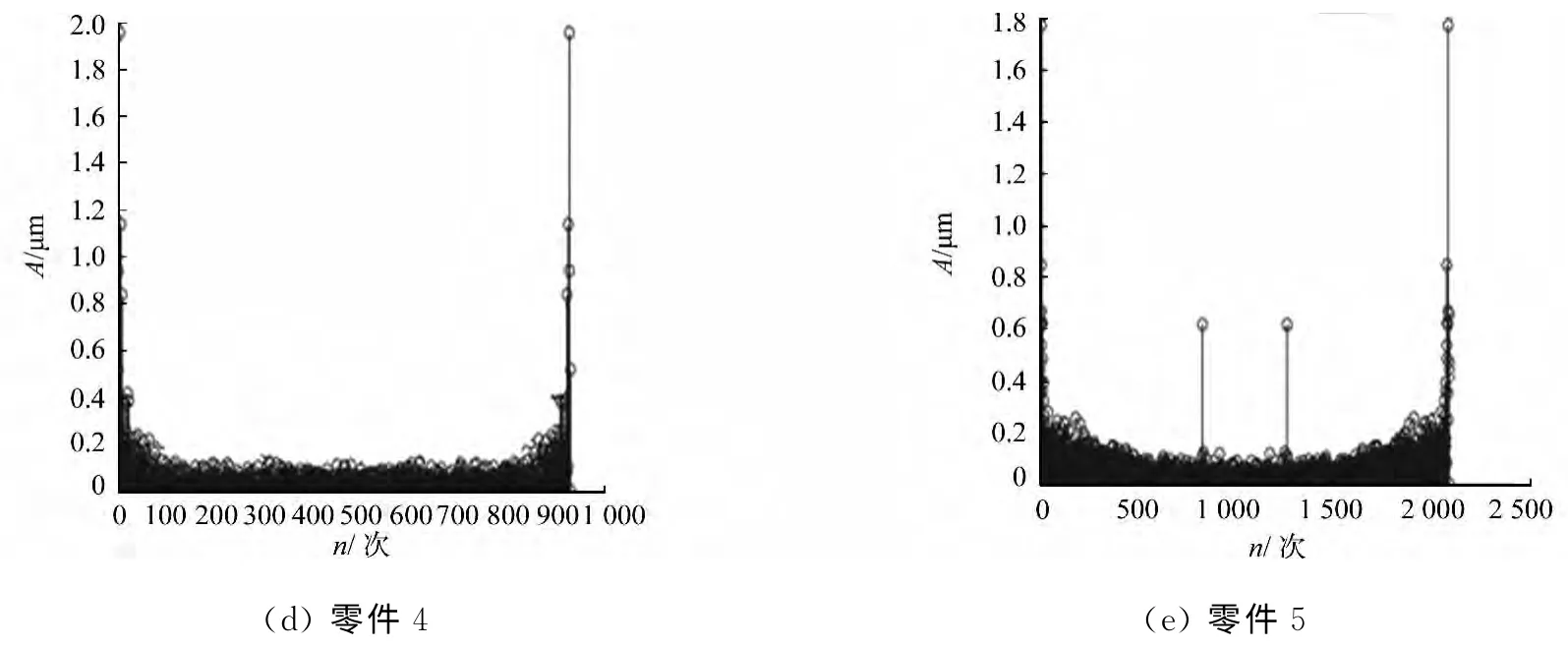
圖2 零件的直線度誤差諧波分析圖Fig.2 Straightness error of parts by harmonic analysis

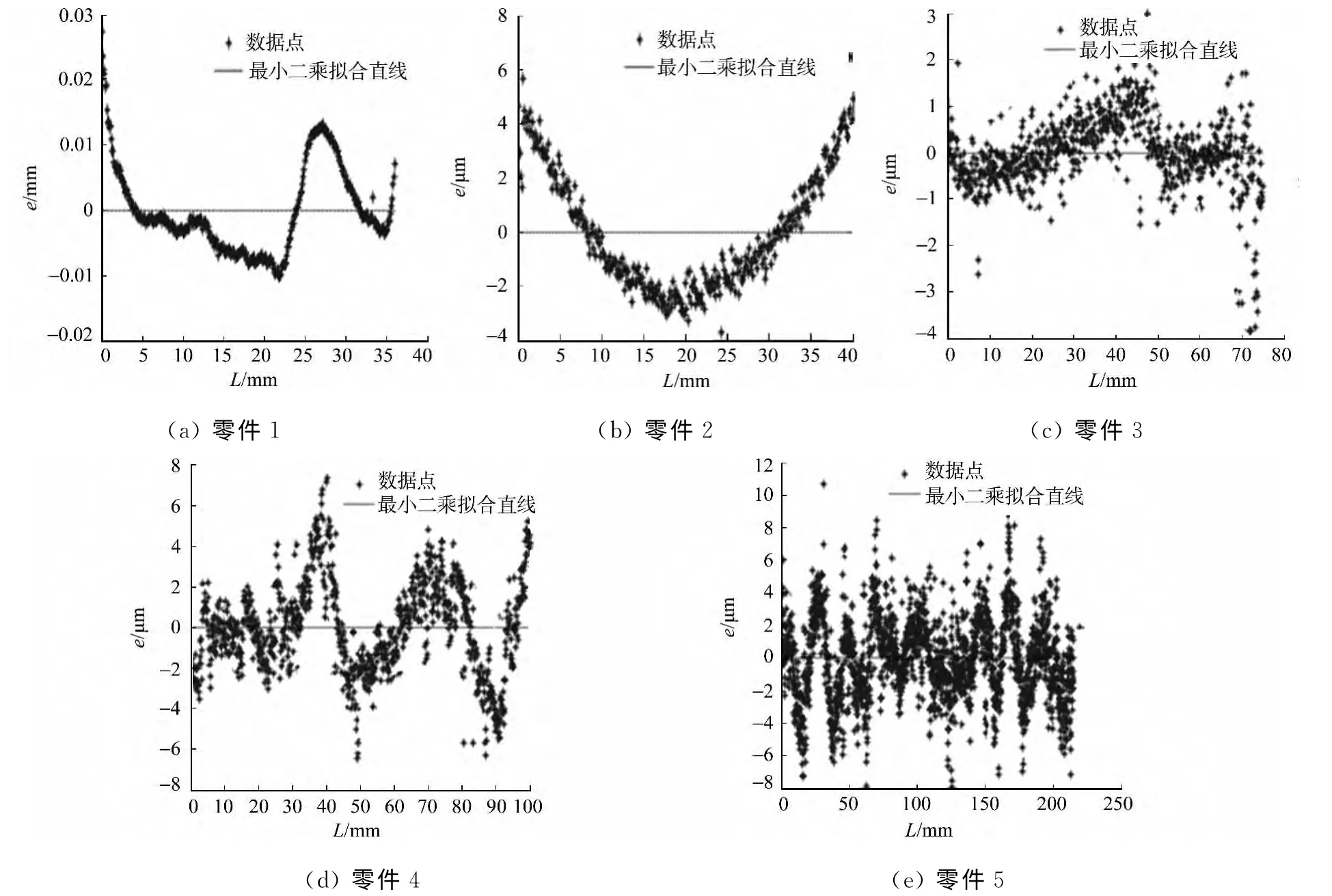
圖3 直線度誤差測量點的分布圖Fig.3 Distribution diagram of straightness error measuring point

由圖3可知：直線度誤差信號都呈現出隨機性誤差和確定性誤差相疊加的特征，且兩者在直線度誤差中所占的比例各有不同.如零件1呈現出以確定性誤差為主，隨機性誤差為輔的特征，而零件5則是隨機性誤差為主，確定性誤差為輔的特征.因此，可以將這兩部分誤差進行分離，對確定性誤差以上所述的諧波分析原理進行諧波分析，可以得到使用奈奎斯特采用定理所需要的最高次諧波波長，并確定出最佳提取點數.

隨機性誤差由于理論上其服從正態分布的規律，可以采用計算機仿真的方法確定出最佳提取點數.將兩部分確定得到的最佳提取點數進行比較，確定出最終的最佳提取點數.

3 結論

正確識別直線度誤差信號的諧波波長成分，是直接應用奈奎斯特采樣定理確定直線度誤差提取點數的前提.通過三坐標測量機上對零件平面內直線度誤差的測量實驗以及諧波分析發現，在得到的諧波分析圖上無法找到直線度誤差信號的最高次的諧波波長成分，充分表明相關標準中建議采用的奈奎斯特采樣定理無法直接用于確定直線度誤差的提取點數.

通過對直線度誤差進行誤差分離處理，對分離出的確定性誤差采用上述的諧波分析的方法，從而再依據奈奎斯特定理確定出提取點數.關于直線度誤差信號的誤差分離，以及誤差分離后提取點數的確定問題將另文詳細介紹.

［1］張琳娜，王銘，鄭玉花.新一代GPS中提取與濾波、擬合操作間關聯特性的研究［J］.機械強度，2010，32（2）：293－298.

［2］中華人民共和國國家質量監督檢驗檢疫總局，中國國家標準化管理委員會.GB／T 1958－2004產品幾何量技術規范（GPS）形狀和位置公差 檢測規定［S］.北京：中國標準出版社，2004：80－165.

［3］張琳娜，鄭玉花，鄭鵬.基于GPS的提取操作模型及其應用規范研究［J］.機械強度，2007，29（4）：632－636.

［4］鄭玉花，張琳娜，慶科維.新一代GPS的提取方案及其應用研究［J］.機械設計與制造，2008（6）：193－194.

［5］久曾神煌.真圖度測定精度與測定點數的關系［J］.精密機械，1984，50（12）：67－70.

［6］費斌，范裕健，徐文雄，等.一種用于形狀誤差測量的采樣新方法：自適應采樣法［J］.應用科學學報，1994，12（4）：423－430.

［7］趙前程，鄧善熙，丁興號，等.圓度測量中測量點數的確定［J］.農業機械學報，2004，35（1）：136－140.

［8］AFFAN BADAR M，RAMAN S，PULAT P S.Intelligent search－based selection of sample points for straightness and flatness estimation［J］.Manuf Sci Eng，2003，125（2）：263－271.

［9］RAGHUNANDAN R，RAO P V.Selection of an optimum sample size for flatness error estimation while using coordinate measuring machine［J］.Mach Tools Manuf，2007，47（3／4）：477－482.

［10］何改云，宋占杰.三坐標法測量球度誤差時最佳測點數目的確定［J］.工具技術，1999，33（9）：27－28.

［11］趙光宙.信號分析與處理［M］.2版.北京：機械工業出版社，2007：24－45.

［12］黃麗玲，黃富貴.直線度誤差統計模型識別的實驗方法［J］.華僑大學學報：自然科學版，2013，34（1）：1－4.