引入虛擬電抗的獨立運行微電網改進下垂控制

黃春燕

(南通供電公司，江蘇 南通 226000)

微電網是解決分布式電源（DG）并網的有效途徑[1]。根據不同種類微電源的輸出特性，微電源的控制方法有下垂控制、PQ 控制和Vf 控制[2]。下垂控制模擬傳統發電機的下垂特性來實現并聯控制，利用P-f和Q-V下垂特性實現對有功和無功的解耦控制[3]。但P-f和Q-V下垂控制適用的一個前提條件是線路的電抗X 遠大于其電阻R，而在低壓微電網中線路電阻值通常大于線路電抗值，功率傳輸P-f和Q-V的對應關系不再存在，逆變型微電源并聯運行采用下垂控制將無法實現功率的正確分配。

為避免功率控制耦合現象，有些學者提出虛擬同步旋轉軸的解耦控制策略[4]。文獻[5]提出虛擬有功無功傳輸控制的方法，利用正交矩陣變換將實際的PQ 值轉換為虛擬PQ 值。文獻[6]提出可以在逆變電源輸出端和負載之間串聯一個大的電感或者安裝隔離變壓器，以保證逆變電源到負荷之間的阻抗為感性，這樣P-f和Q-V下垂控制的前提條件就能夠滿足了，但是電感的投入增加了系統的體積和成本，當輸出電流中含有高次諧波成分時，電感上將產生很大的諧波壓降，從而使輸出電壓失真嚴重。文獻[7]通過設計控制器參數使輸出阻抗呈感性，但是阻抗大小不能確定。

1 DG 并網逆變器結構及控制原理

1.1 DG 并網逆變器結構

微電網由DG、儲能裝置、負荷、傳輸線路和控制系統等元件和模塊組成。絕大多數DG 通過逆變或者整流/逆變的電力電子變換器接入微電網母線。假設DG 直流側裝設有儲能裝置，因此可將DG 并網逆變器側電壓視為一個恒定值，則DG 并網逆變器結構如圖1 所示。

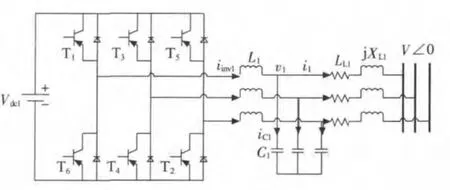
圖1 DG 并網逆變器結構

圖1 中，Vdc1為DG 直流側電壓；iinv1為并網逆變器交流側輸出電流；L1為濾波電感；v1為濾波電容電壓，也是DG 輸出電壓（忽略濾波電阻）；iC1為濾波電容電流；C1為濾波電容；i1為DG 輸出電流；RL1為DG 并網傳輸線電阻；XL1為DG 并網傳輸線電抗；為微電網交流母線電壓。

1.2 并網逆變器控制原理

逆變器控制方法由最初的無環控制[8]，改進成單環控制[9]，現在常采用電壓電流雙環控制[10，11]。選擇濾波電容電流作為控制變量構建電流內環，選取濾波電容電壓作為控制變量構建電壓外環。電壓外環能夠保證DG輸出電壓的穩定，同時給電流內環提供電流參考值；電流內環按照電壓外環輸出的電流參考值進行電流控制，對非線性負載擾動的適應能力增強，輸出電壓的諧波含量小。電流內環采用比例（P）控制，電壓外環采用比例—積分（PI）控制，簡化的雙環控制系統結構如圖2 所示。

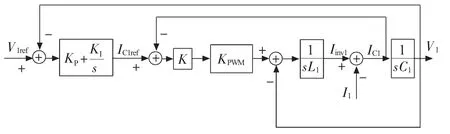
圖2 簡化的雙環控制系統結構

圖2 中，KP，KI是外環比例積分系數，K 是內環比例系數，KPWM是逆變器放大系數。以V1ref為輸入，V1為輸出，可以得到電壓環傳遞函數：

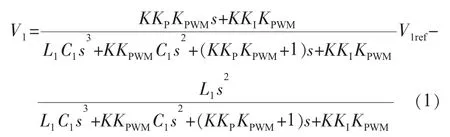
該傳遞函數的前半部分體現了控制系統的穩定性，后半部分體現了負載電流所產生的擾動的影響，可簡化為：

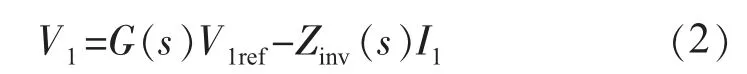
式（2）中：G（s）為電壓比例增益傳遞函數，理想情況下G（s）=1；Zinv（s）為逆變器等效輸出阻抗。

由式（1）可知，Zinv（s）不僅與濾波器參數有關，還與控制器參數有關，當濾波器參數確定時，可以通過設計合適的控制器參數，使Zinv（s）呈感性或阻性。由圖2可得電壓環的開環傳遞函數：

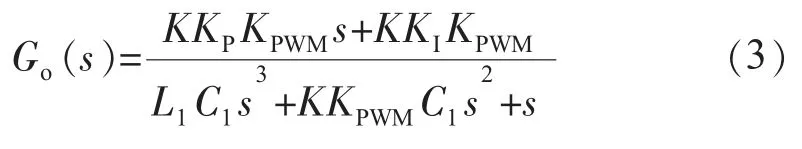
2 基于控制器參數設計的下垂控制

2.1 下垂控制原理

以2個電源并聯運行為例分析下垂控制原理，如圖3 所示。

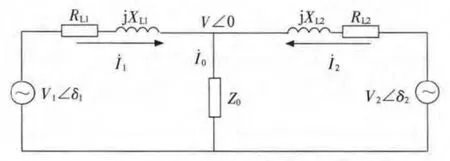
圖3 功率傳輸示意圖

圖3 中，設Vk∠δk為第k個電源的輸出電壓，k=1，2，…；RLk和XLk分別為第k個電源的并網傳輸線電阻和電抗；V∠0為負荷端交流母線電壓，也是負載Z0上的電壓；I˙k為第k個電源的輸出電流，I˙0為負載電流。第k個電源輸出的有功功率和無功功率分別為：

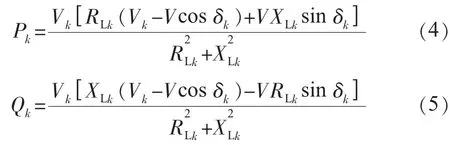
在高壓輸電系統中，傳輸線路電抗遠大于電阻，即XLk>>RLk，可以將RLk忽略，并且功率角δk很小，可近似得到sin δk≈δk，cos δk≈1，則式（4）和式（5）化簡為：

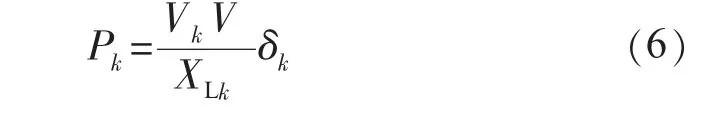
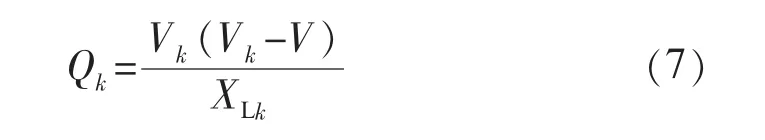
在低壓配電系統中，傳輸線路電阻通常大于電抗，即RLk>XLk；考慮到功率角δk通常很小，則式（4）和式（5）化簡為：

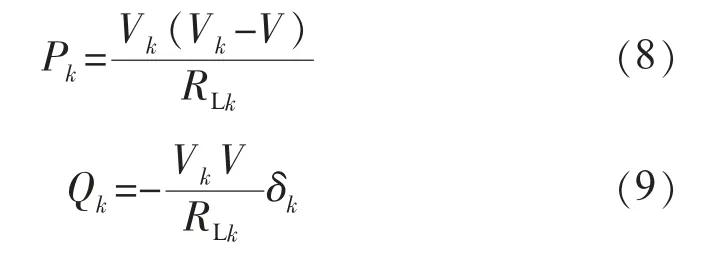
由此可見，低壓、高壓系統的功率傳輸表達式有所不同，從而下垂控制的表達式也有所不同。當線路傳輸線阻抗中電抗遠大于電阻時，采用有功-頻率（P-f）和無功-電壓（Q-V）的解耦控制方式；反之采用有功-電壓（P-V）和無功-頻率（Q-f）的解耦控制方式。根據線路的阻抗特性，選擇正確的下垂控制方式才能實現有功無功的解耦控制。

2.2 下垂控制的不足

微電網屬于低壓配電網范疇，傳輸線路呈阻性，根據上文的分析，宜采用P-f和Q-V的反調差下垂控制方式，但是現有的逆變電源下垂控制方法大多采用P-f和Q-V的傳統下垂控制方式。設置控制器的參數，使其既能保證控制系統的穩定性，又能保證控制系統具有一定的穩態和動態性能指標，同時還能保證在工頻附近逆變器等效輸出阻抗Zinv（s）呈感性，并且該值與線路實際阻抗之和也呈感性。取濾波器參數L=0.8 mH，C=1600 μF，為了得到合適的控制器參數，采用經驗法[12]和頻域響應曲線相結合，得到控制器參數K=0.6，KP=10，KI=100時，Zinv（s）呈感性，此時Zinv（s）的頻域響應曲線如圖4 所示。可以看出，逆變器等效輸出阻抗Zinv（s）在50 Hz 附近呈感性，在高頻段呈阻性。

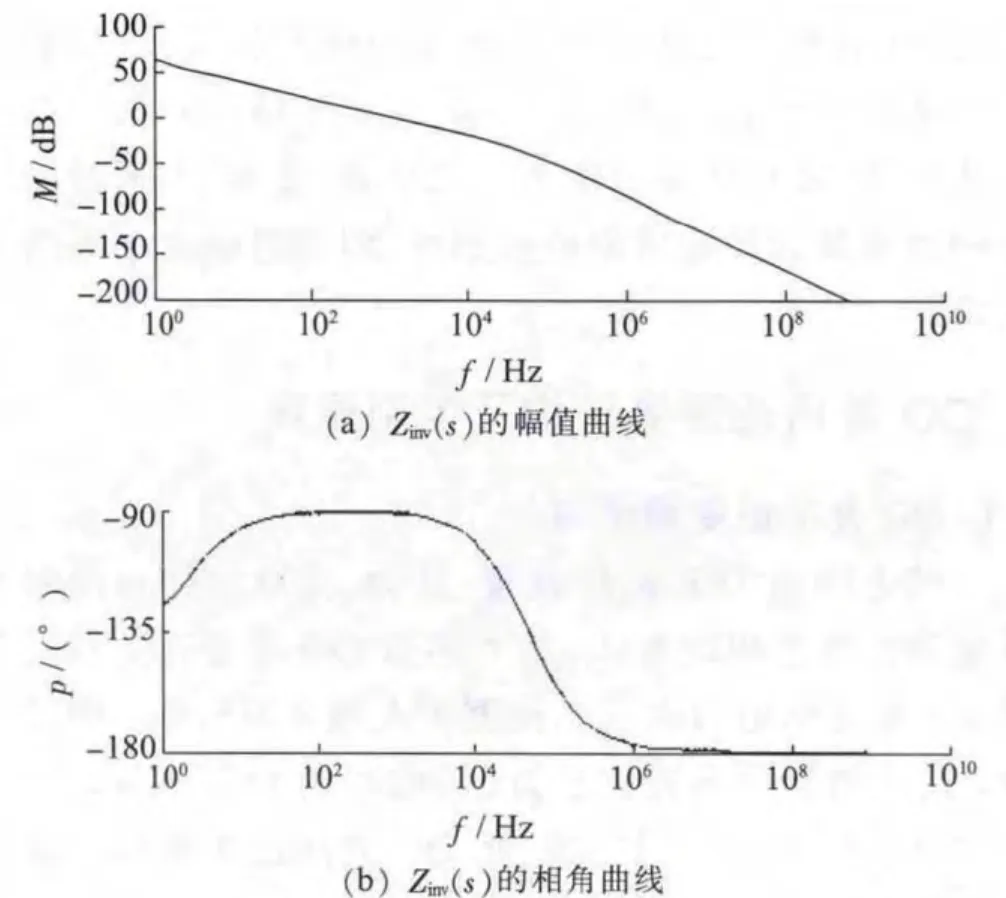
圖4 Zinv(s)的頻域響應曲線

此時，電壓環的開環傳遞函數Go（s）的波特圖如圖5 所示。從圖5 可知系統穩定，具有一定的幅值裕度和相位裕度。

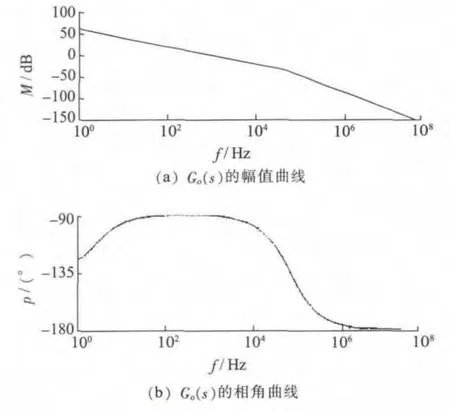
圖5 Go(s)的波特圖

以上分析表明，整定的K，KP，KI既能夠滿足系統控制性能的要求，也能保證逆變器等效輸出阻抗Zinv（s）呈感性。接下來分析Zinv（s）的數值大小，將L，C，K，KP，KI值代入Zinv（s）計算公式，令s=j314，求得頻率為50 Hz時逆變器等效輸出阻抗：

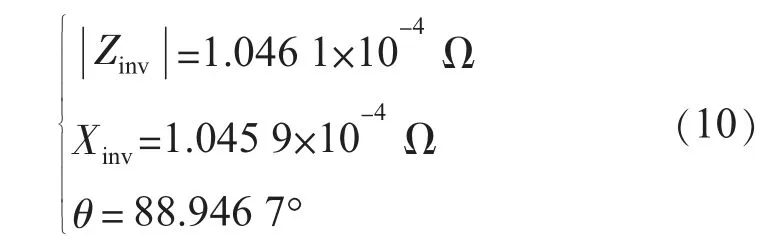
由式（10）可見，此時逆變器的等效輸出電抗值非常小，不足以使線路具有高壓輸電線路的特性。保持L和C 值不變，在K∈[0.001，10]，KP∈[0.001，1000]，KI∈[0.001，3000]的范圍內尋找Xinv的最大值為：當K=0.001，KP=0.001，KI=159時，=0.287 3。但是，此時K 值很小，控制系統的快速性很差，如果外界發生一個小擾動，則系統達到穩定狀態所耗費的時間很長。其次，如果逆變電源與負載之間的實際低壓線路長度較長，則該值就不足以使可控電源與負載之間的等效線路阻抗具有高壓線路的感性性質。

以上分析表明，控制器參數設計法不能同時滿足系統性能和逆變器等效輸出阻抗值的要求，所以本文引入虛擬電抗的思想對下垂控制加以改進。

3 引入虛擬電抗的改進下垂控制

為了使逆變電源與負載之間的輸出阻抗呈感性，又不在逆變器的輸出端真正接入一個電感，可以采用“虛擬電抗”的概念，在逆變器的輸出端模擬出一個遠大于逆變器到負載之間電阻的虛擬電抗[13]。通過在逆變電源電壓電流雙環控制的電壓指令值中減去虛擬電抗上的壓降來實現模擬出一恒定的電抗，記虛擬電抗為Xvir，得到新的電壓參考值：

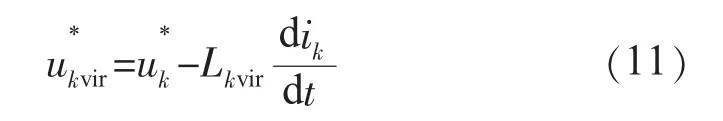
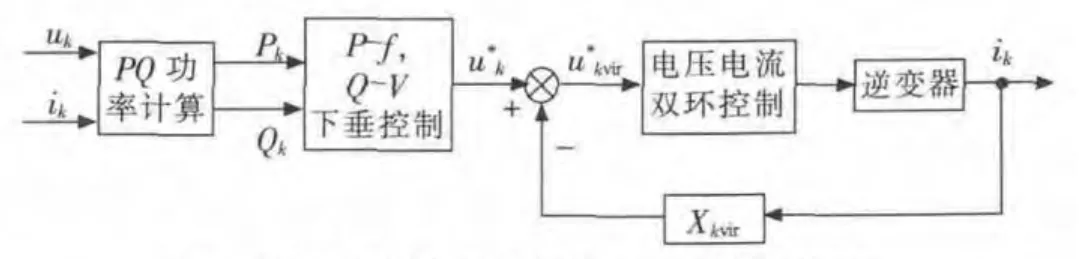
圖6 引入虛擬電抗后的閉環系統控制框圖

此時逆變器電壓環傳遞函數：

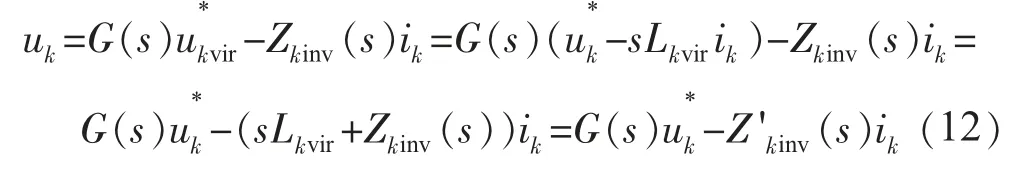
由式（12）可以看出，等效輸出阻抗Z'kinv（s）=sLkvir+Zkinv（s），當Lkvir取遠大于逆變器到負載電阻值時，就可確保線路阻抗呈感性，而且電流電壓環參數的設計確保了Zkinv（s）對于基頻呈感性，進一步增大了等效電抗。采用虛擬電抗法將逆變電源與負載之間的電抗值加以改變，可以保證線路阻抗主要呈感性，滿足了下垂控制的前提條件，但是也犧牲了系統輸出電壓的穩態精度，輸出電壓值較未采用虛擬電抗法時有所下降。因此，可對下垂特性曲線進行改進，將虛擬電抗上的壓降納入考慮范圍，以提高輸出電壓穩態精度[13]。因虛擬電抗上不消耗有功功率，只消耗無功功率，所以只需修正Q-V下垂特性曲線。定義逆變電源輸出電壓和負載電壓之差ΔVk與逆變電源發出的無功功率Qk之比為Kk。引入虛擬電抗后，線路呈感性，按式（7）可得：

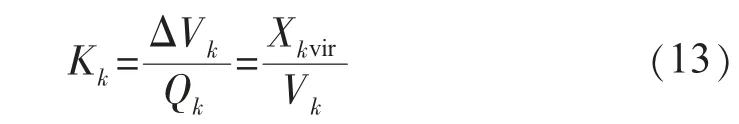
由于需控制Vk在一定范圍內變化，一般為額定值的±5%，且Xkvir為設定的電抗值，所以Kk可近似視為一恒定值。2個逆變電源修正前Q-V下垂系數分別為n1和n2，最大無功功率輸出為Q1max和Q2max，允許電壓最小值為Vmin。如圖7 所示。

當2個逆變電源均發出最大無功功率時，Xkvir上的壓降為KkQkmax，從而將Q-V下垂特性曲線的電壓最小值修正為：

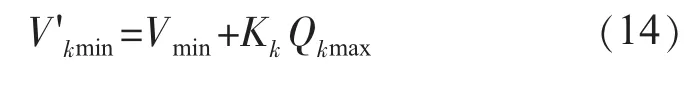
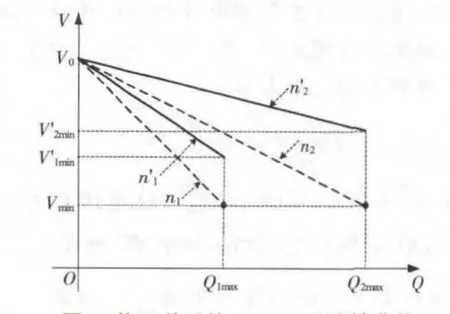
圖7 修正前后的Q-V 下垂特性曲線

由此可得修正下垂特性曲線的Q-V下垂系數為：

此時下垂特性曲線的表達式：

將修正后的下垂特性曲線用在圖6 中，有利于提高電壓穩態精度。

綜上所述，引入虛擬電抗后，可以保證逆變電源到負載之間的線路阻抗呈感性，從而P-f 和Q-V下垂特性曲線能夠正確實現功率分配；采用修正后的下垂控制曲線提高了電壓的穩態精度。

4 仿真分析

為了驗證基于虛擬電抗的改進下垂控制的有效性，將傳統的下垂控制與基于虛擬電抗的改進下垂控制進行仿真對比。采用的微電網仿真系統結構如圖8所示。

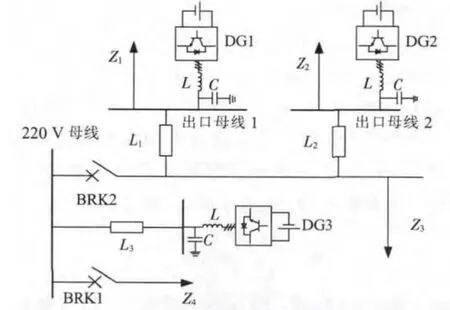
圖8 微網仿真系統結構

圖8 中，3個DG 并聯運行，額定電壓Vdc為800 V，容量均為10 kW，母線電壓等級為220 V；線路1，線路2，線路3的長度分別為200 m，300 m，200 m，線路單位阻抗參數為r=0.641 Ω/km，x=0.101 Ω/km（電抗參數為工頻值）；負荷采用恒阻抗模型，參數設置為Z1=Z2=（50+j3.14）Ω，Z3=Z4=（30+j12.56）Ω。

設3個DG的P-f 下垂系數m1:m2:m3=4×10-5:6×10-5:12×10-5=2:3:6，Q-V 下垂系數n1:n2:n3=3×10-5:3×10-5:3×10-5=1:1:1，3個DG的控制器參數：L=0.6 mH，C=1500 μF，RL=0.01 Ω，K=0.6，KP=10，KI=100。

4.1 傳統下垂控制仿真

DG1，DG2，DG3 均采用傳統下垂控制，t=2 s時，開關BRK1 閉合，負荷Z4投入，仿真結果如圖9 所示。

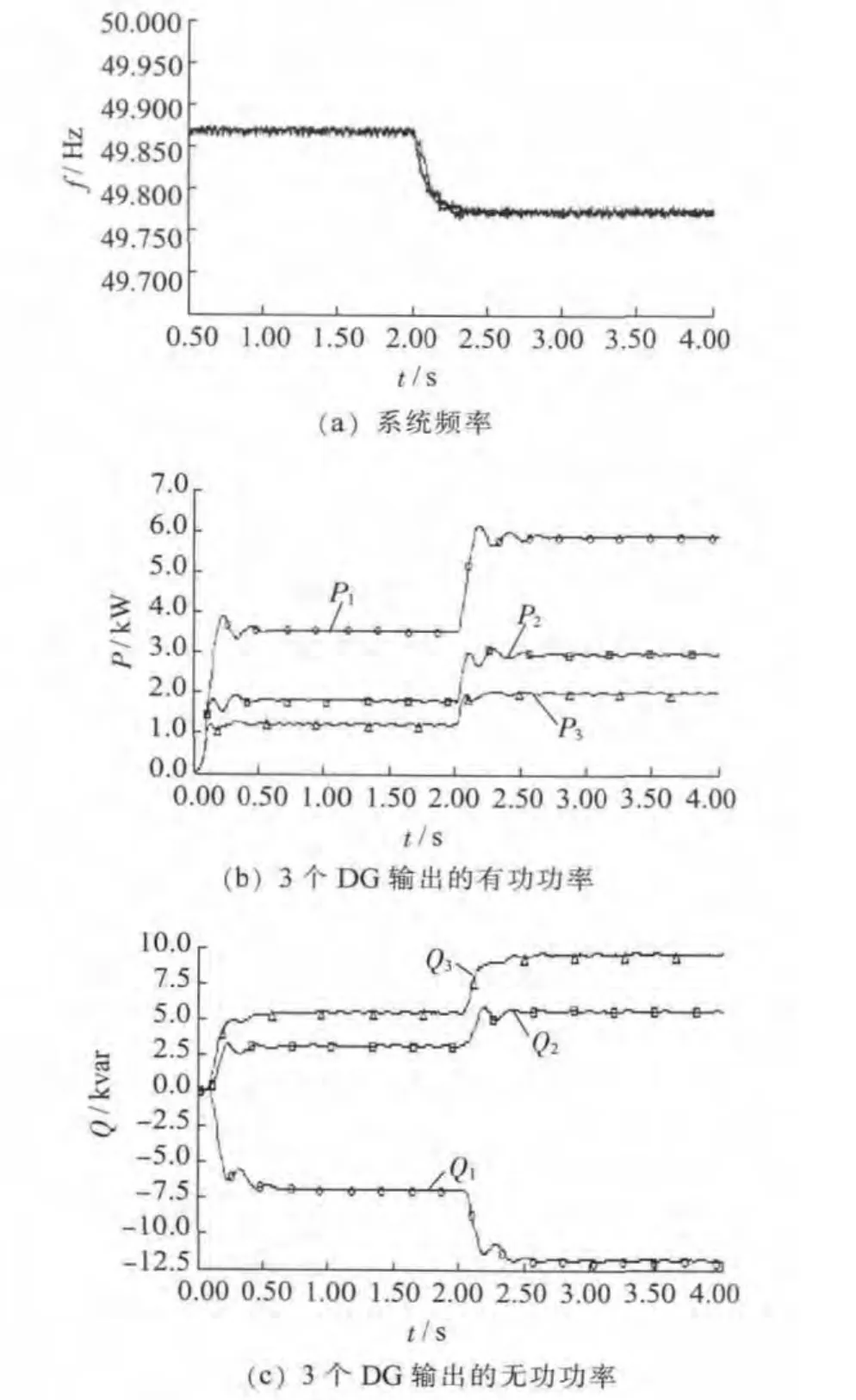
圖9 傳統下垂控制仿真結果

仿真啟動后微網很快達到穩定。由圖9（a）可知，f1=f2=f3，即3個DG的頻率輸出一致，則微網的頻率唯一，否則微網一直處于頻率不穩定狀態。t=2 s時，負荷Z4投入，3個DG 增加有功出力，系統頻率下降，符合一次調頻特性。由圖9（b）可知，有功出力始終按照有功下垂系數的反比承擔負載有功功率，P1:P2:P3=6:3:2。t=2 s時Z4投入，經過一段時間后，微網再次達到穩定，3個DG 按比例共同承擔新增的負載有功功率，此時仍然有P1:P2:P3=6:3:2。由圖9（c）可知，在整個仿真過程中，無功出現了嚴重的不平衡：DG1 吸收無功，DG2 和DG3 發出無功，3 者之和為負荷所需無功，當Z4投入后，3個DG的無功差別更大。出現上述現象的原因是低壓配電網線路呈阻性時，如式（9）所示，逆變電源輸出的無功功率不僅與電壓幅值有關，而且與相角有關，因而傳統下垂控制失效，無功功率得不到正確分配。

4.2 基于虛擬電抗的改進下垂控制仿真

DG1，DG2，DG3 采用基于虛擬電抗的改進下垂控制，取L1vir=L2vir=L3vir=4 mH，t=2 s時負荷Z4投入，仿真結果如圖10 所示。

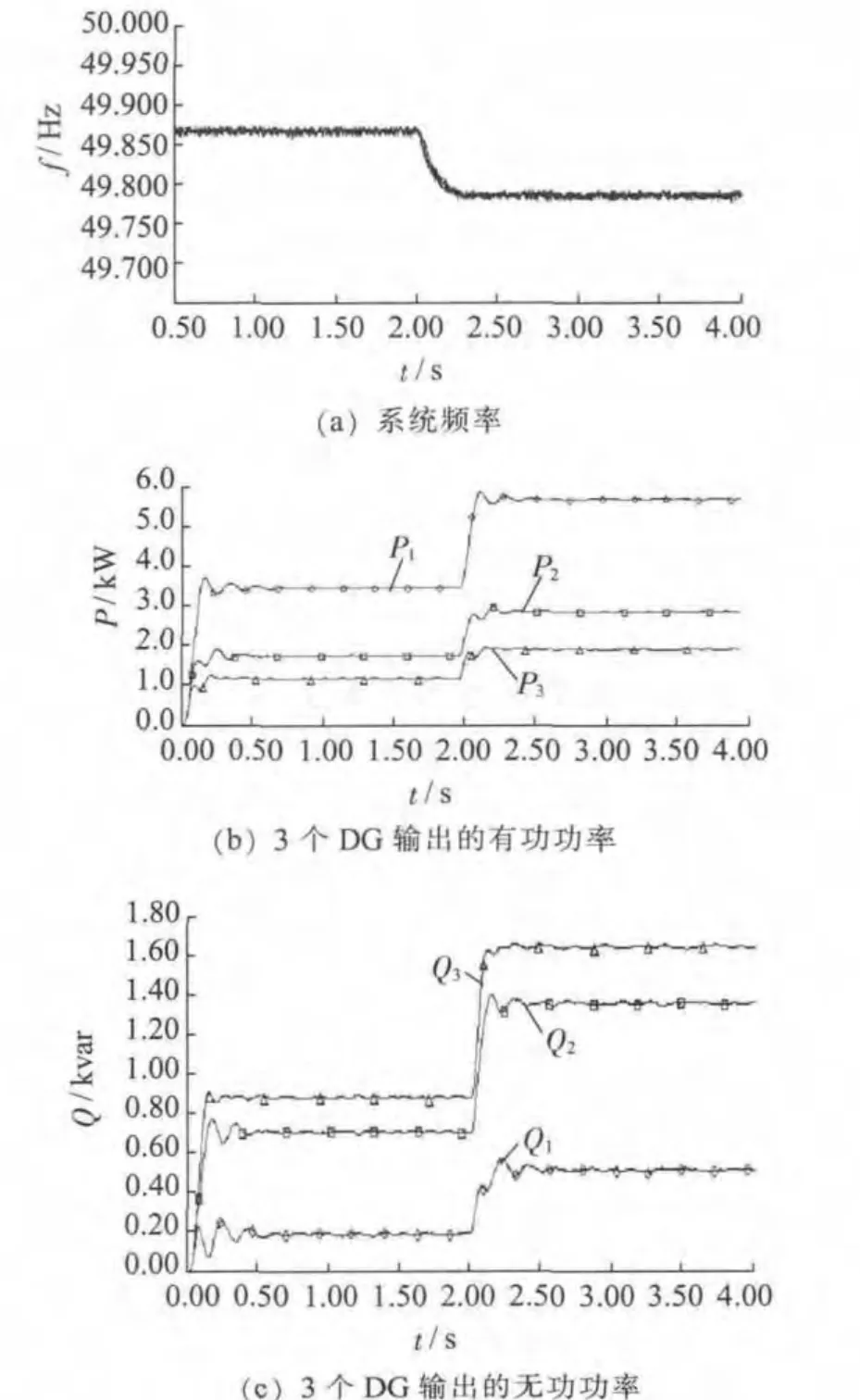
圖10 基于虛擬電抗的改進下垂控制仿真結果

由圖10 可知，3個DG 均采用基于虛擬電抗的改進下垂控制之后，微網同樣能夠穩定運行。圖10（a）表明，3個DG的頻率輸出一致；圖10（b）表明，3個DG始終按有功下垂系數的反比共同承擔負載有功功率。圖10（c）表明，采用基于虛擬電抗的改進下垂控制后，DG1，DG2，DG3 能較好地實現無功負荷的均分，所發出的無功均為正值，避免了部分發出無功，部分吸收無功的情況。值得注意的是，雖然引入了虛擬電抗且n1:n2:n3=1:1:1，但Q1:Q2:Q3≠1:1:1，其原因有2 點：（1）雖然修正了下垂特性曲線，將虛擬電抗上消耗的無功納入了考慮范圍，但是只是采取了近似計算方法，由下垂特性曲線計算出來的電壓參考值精度降低了；（2）實際線路的長度不一致，當各個逆變電源的輸出外特性和線路阻抗不一致時，僅利用Q-V 下垂控制是無法實現DG 輸出無功嚴格按無功下垂系數的反比分配的，即使在線路為純感性的情況下也是如此，這一點有別于P-f下垂控制。3個DG 輸出的電流與采用傳統下垂控制時相比，均有所下降，如表1 所示。

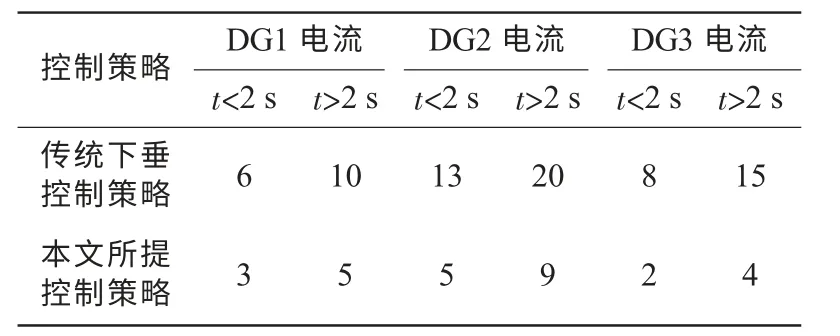
表1 2 種控制方法電流比較 A

由表1 可知，改進下垂控制使得無功能在DG 中合理分配，避免了某些DG的無功過載，因此大大降低了線路電流。

5 結束語

P-f和Q-V 下垂控制能實現功率分配的前提條件是線路呈感性。分析表明，通過設計控制器參數使得微電網中線路呈感性的方法不能同時滿足系統性能和逆變器等效輸出阻抗值的要求。因此，基于虛擬阻抗的思想，在逆變電源的輸出端模擬出一個遠大于逆變器到負載之間電阻的虛擬電抗，確保線路呈感性，從而滿足了P-f和Q-V 下垂控制的應用條件。仿真表明，該方法可以確保P-f和Q-V 下垂控制在阻性線路環境中有較好的功率分配效果，驗證了該方法的有效性。

[1]魯宗相，王彩霞，閔 勇，等.微電網研究綜述[J].電力系統自動化，2007，31(19)：25-34.

[2]王成山，肖朝霞，王守相.微網綜合控制與分析[J].電力系統自動化，2008，32(7)：98-103.

[3]肖朝霞，王成山，王守相，等.含多微型電源的微網小信號穩定性分析[J].電力系統及其自動化，2009，33(6)：81-85.

[4]朱永利，姚建國，劉 驥.微電網關鍵技術及研究現狀.江蘇電機工程[J].2012，31(3)：81-84.

[5]BRABANDERE K D,BOLSENS B,DEN KEYBUS J V,et al.A Voltage and Frequency Droop Control Method for Parallel Inverters[J].IEEETransonPowerElectronics,2007,22(4):1107-1115.

[6]GUERRERO J M,MATAS J,VICU?A L G,et al.Decentralized Control for Parallel Operation of Distributed Generation Inverters Using Resistive Output Impedance [J].IEEE Trans on Industry Electronics,2007,54(2):994-1004.

[7]王成山，肖朝霞，王守相.微網中分布式電源逆變器的多環反饋控制策略[J].電工技術學報，2009，24(2)：100-107.

[8]ENGLER A.Applicability of Droops in Low Voltage Grids [J].International Journal of Distributed Energy Resources,2005,01(1):1-6.

[9]LASSETER R H.Microgrids and Distributed Generation[J].Journal of Energy Engineering American Society of Civil Engineers,2007,133(3):144-149.

[10]HERNANDEZ-ARAMBURO C A,GREEN T C.Fuel Consumption Minimization of a Microgrid [J].IEEE Trans on Industry Applications,2005,41(3):673-681.

[11]陳 波，朱凌志，朱曉東.并網光伏電站低電壓穿越仿真與分析[J].江蘇電機工程，2012，31(5)：13-17.

[12]薛亞麗，李東海，徐 峰，等.最優PI 控制器參數整定及評價[J].清華大學學報（自然科學版），2004，44(8)：1067-1070.

[13]LI Y W,KAO C N .An Accurate Power Control Strategy for Power-electronics-interfaced Distributed Generation Units Operating in a Low-voltage Multibus Microgrid [J].IEEE Trans on Power Electronics,2009,24(12):2977-2988.