彈道再入目標軌跡跟蹤中非線性濾波算法研究＊

田亞菲 莫 驊 于 飛

（1．蘭州大學信息學院 蘭州 730000）（2．總參謀部通信訓練基地 張家口 075100）

1 引言

彈道再入目標的軌跡跟蹤問題一直以來受到人們的普遍關注，它是彈道導彈防御系統的核心技術，直接影響對來襲導彈攔截的成功率。針對跟蹤目標的動力學模型和雷達的觀測模型具有典型的非線性特性，國內外相關文獻提出許多非線性濾波算法，在算法選擇上存在明顯不同的觀點［1～3］。常見的算法中，大致可分為兩大類［4］：一類是基于點的濾波算法，主要包括擴展卡爾曼濾波器（EKF）和無跡卡爾曼濾波器（UKF）及對應的改進算法；另一類是基于密度的濾波算法，包括貝葉斯粒子濾波器（PF）及對應的改進算法。

本文依據彈道再入目標動力學模型和雷達觀測模型特點，從算法基礎理論出發對比分析EKF和UKF算法的異同點，通過仿真實驗全面比較了EKF、UKF和PF三種基本算法的性能，得出到在高斯噪聲條件下，EKF要優于UKF和PF，在閃爍噪聲條件下，PF要優于EKF和UKF的結論。

2 基于點的濾波算法理論

2．1 線性遞歸估計算法的基本思想

本質上講，EKF和UKF在狀態更新階段是一個基于最小均方誤差（MMSE）條件下的線性遞歸估計算法。一個非線性動態系統的狀態方程和觀測方程可用下面兩式來描述。

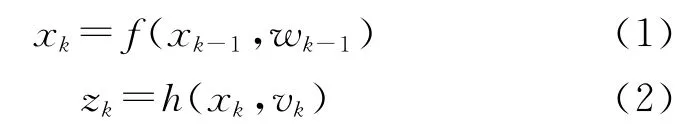
使用線性回歸估計方法可以從當前觀測值zk中估計出k時刻的狀態變量xk，其中經典的算法是線性最小均方誤差估計法（LMMSE）。觀測值序列的概率密度函數未知的平穩過程在前二階矩已知的條件下，可以通過遞歸迭代的算法完成估計，此時基于觀測值的估計是觀測值的線性變換。若符合高斯約束條件時，LMMSE算法是基于MMSE約束條件下的最優估計。

用zk表示從初始時刻到k時刻所得到的一組觀測數據，LMMSE 估計中E＊xk｜zk具有如下解析形式［5］：

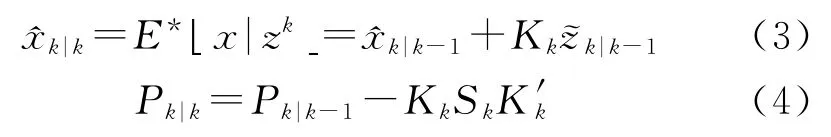
如果以上式中狀態一步預測、一步預測誤差協方差，觀測值預測、觀測預測估計協方差Sk，狀態估計值與觀測估計值互協方差都能通過給定的k-1時刻的狀態估計值和誤差協方差Pk-1｜k-1（即初值）求出，此LMMSE算法就是真正意義上的遞歸運算。若系統的動力學方程和觀測方程能滿足線性和高斯條件，以上計算公式就是著名的kalman濾波算法。

對于具有觀測方程（2）的非線性系統

和都依賴于k-1時刻以前的觀測值zk-1和相應時刻LMMSE 估計值。為實現真正的遞歸線性估計，要求k時刻的估計值僅從和Pk-1｜k-1就能求得，即：

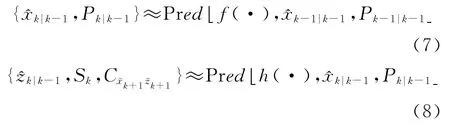
以上兩式中，Pred f（·），，Pk-1｜k-1表示｛，Pk-1｜k-1｝通過非線性函數f（·）的傳遞作用來近似得到一步狀態預測值和對應的協方差Pk｜k-1。Pred h（·），，Pk｜k-1表示 通過狀態預測值來近似得到觀測預測值和相應的誤差矩陣。近似運算由于舍棄了部分信息，從而導致信息傳遞的不完整，使非線性濾波器的性能發生退化。通常采用兩種方法來克服近似運算帶來的弊端：一是盡可能地使用最優的近似，這樣就能避免過多的舍棄信息，保證預測的準確性，例如采用高階的泰勒級數展開方法（TSE）；另外一種方法是用一種適當的分布來逼近非線性函數而不進行舍棄，這樣的預測中包含了所有非線性系統的統計信息，例如無跡變換方法（UT）［6］。

無論觀測方程是否滿足線性條件，只要能實現非線性系統的近似線性化，得到預測值的一階矩和二階矩信息，LMMSE估計器就可以非常理想地直接應用在非線性系統的狀態更新上，這就是EKF和UKF本質上相同之處。兩者的區別僅在于在式（7）～式（8）中對非線性系統的近似處理上采用不同的策略。

2．2 EKF的線性化策略

EKF的近似策略是對非線性函數的Taylor展開式進行一階或二階的線性化截斷，忽略高階項。假設過程噪聲和量測噪聲是0均值且互不相關的的高斯噪聲，在一階EKF中，非線性系統的狀態方程（1）和觀測方程（2）通過以下的步驟完成線性化：

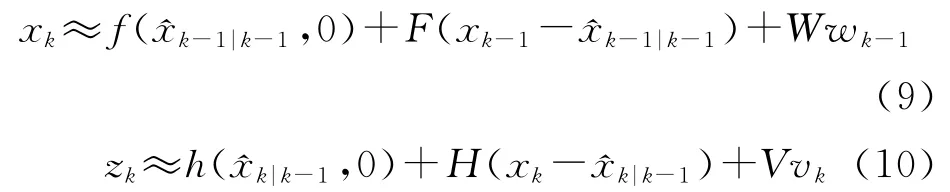
F和H分別是函數f（·）和h（·）對狀態變量x求偏導的雅克比矩陣，即和W和V分別是函數f（·）和h（·）分別對過程噪聲w和量測噪聲v求偏導數的雅克比矩陣，即W［i，j］＝根據以上線性化變換，預測及狀態更新過程描述如下

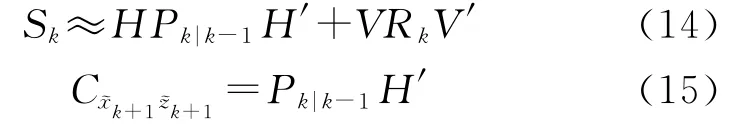
式（11）～式（15）與LMMSE 的遞歸線性運算式共同構成了一階EKF算法公式。

EKF的估計精度嚴重依賴于系統的非線性程度。為提高近似精度，可采用二階EKF。雖然二階EKF可以比一階EKF獲得更好的濾波性能，但是計算量較大，同時要求非線性函數的海森矩陣在數學上存在，而在計算海森矩陣中會產生計算誤差。因此，針對彈道再入目標觀測方程的強非線性特性，在EKF線性化近似之前，可以采用坐標系轉換的方式來盡可能地減弱其非線性特性［7］。對于極坐標下所描述的觀測方程，可以通過以下兩式轉化成直角坐標系的方程［8］。

轉化后的觀測變量成為偽線性的形式，減弱了雷達觀測變量在初始極坐標系下的非線性程度。

2．3 UKF的線性化策略

在基于近似非線性函數的概率分布比近似其本身更容易［9～10］的思想指導下，Julier等提出了基于unscented transformation的Kalman濾波算法，即UKF。x為nx維的隨機變量，y＝g（x）是一個非線性變換，假設x的均值和方差分別表示為和Cx，算法描述如下：

第一步：計算sigma點的值χi及其權重Wi：

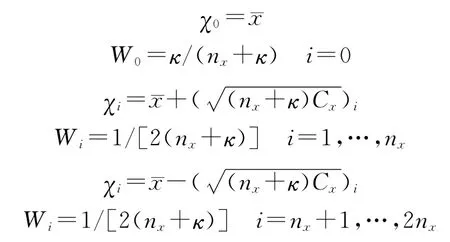
其中κ是縮放比例系數，是矩陣（nx＋κ），Cx的方根的第i行（列）。

第二步：通過非線性函數傳播sigma點：

第三步：計算y的均值和方差，以及x和y的協方差：

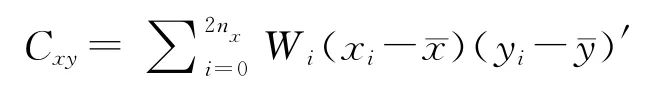
非線性系統的狀態方程（1）和觀測方程（2）通過UT 完成線性化變換：

和分別表示在k-1 時刻預測值和更新值，和是在k-1時刻過程噪聲和觀測噪聲。狀態更新階段同EKF一樣使用LMMSE估計算法。

盡管采用有限個采樣點簡化了近似過程，但是計算采樣點的方根運算增加了計算量，且根式中的矩陣一旦失去正定勢必導致濾波器發散。

3 基于密度的PF算法理論

Gordon和Salmond在1993年提出了一種基于序列重要抽樣濾波思想的Bootstrap非線性濾波方法［11］，從此奠定了粒子濾波（PF）算法的基礎。該算法的基本原理是對于一個平穩的時變動態系統，設k-1時刻系統的后驗概率密度為p（xk-1｜zk-1），根據一定的原則選擇n個隨機樣本點（粒子），k時刻獲得觀測信息后，經過預測更新和狀態更新，n個粒子的后驗概率密度近似為p（xk｜zk），隨著粒子數目的增加，粒子的概率密度函數就逐漸逼近狀態變量的概率密度函數，此時粒子濾波器的估計就達到了最優貝葉斯估計的效果［12］。

基本的粒子濾波算法流程如下：

第一步初始化：取k＝0，按p（x0）抽取N個樣本點，i＝1，2，…，N；

第四步歸一化權重：

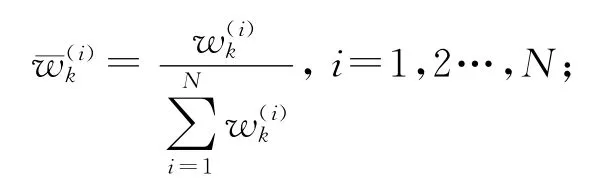
第五步重采樣：根據各自歸一化權重的大小復制或者舍棄樣本，得到N個近似服從p分布的樣本。

進博會食品及農產品展區6萬平方米，分為乳制品、蔬果農產品、肉制品和水產品、休閑食品甜食調味品、酒類和飲料等五大專業展區。徜徉其間，從參觀者身上你會感受到中國對美好生活的追求和向往是那么強烈！中國當自強！中國農業當自強！

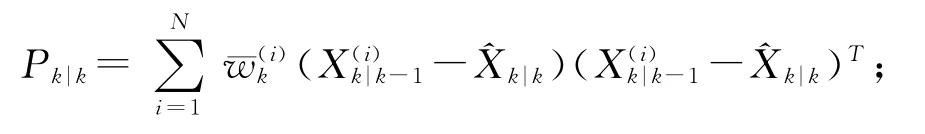
第七步k＝k＋1，重復第二至六步進行迭代運算直到結束。

PF算法通過尋找一組在狀態空間傳播的隨機樣本來對概率密度函數完成近似，以樣本均值代替積分運算，從而獲得狀態變量最小方差分布。它與EKF、UKF不同，對狀態變量沒有高斯約束，因此近年來成為了非線性非高斯系統狀態估計的“最優”估計器。但是PF算法濾波精度與粒子數量、重要性函數、重采樣方法的選取有很大關系［13］。近年來國內外出現了大量的改進算法，但計算量巨大、實時性差的缺點始終未能克服，在一定程度上限制了其在彈道再入目標軌跡跟蹤問題上的工程應用。

4 仿真研究

4．1 彈道再入目標的數學模型及仿真環境描述

在不影響模型精確度的前提下，假定地球表面為平面，目標為質點且不考慮自旋。相關文獻對彈道再入目標的數學模型進行了較為系統的分析［7，14］。本文用如下兩式描述動力學方程和觀測方程。

xk＝［xk，˙xk，yk，˙yk］′是狀態變量，各元素分別表示目標在直角坐標系下x軸和y軸方向上的位置和速度分量。zk＝［rk，θk］′是觀測變量，各元素分別表示雷達對目標的測量距離和角度。wk是過程噪聲，代表觀測噪聲，各元素分別是距離和角度的觀測誤差。假設過程噪聲和觀測噪聲互不相關，且服從不依賴于初值x0的0均值高斯分布，它們的協方差矩陣通過以下三個矩陣式描述，其中Q是過程噪聲協方差矩陣，q是過程噪聲的方差，R是觀測噪聲協方差矩陣。

式（18）中非線性函數Ψ（·）定義為

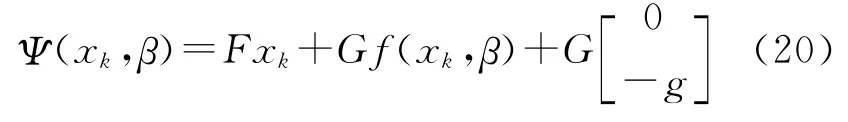
式（20）右端后兩項描述的是空氣阻力和重力對目標狀態變量的影響作用。g是重力加速度，f（xk，β）是空氣動力阻力函數，β為彈道系數，一般的，該系數是時間變量t的函數，即β（t）。文獻［15］討論了參數β（t）的建模方式對非線性濾波算法的性能影響。為簡化模型，本文采用中的彈道系數為確知參數。式（20）中的狀態轉移矩陣F和驅動矩陣G分別表示為

空氣動力阻力函數f（xk，β）定義為式（21）。

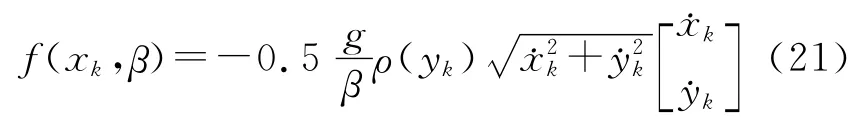
ρ（·）是隨海拔高度呈指數衰落的空氣密度函數。觀測方程中的非線性測量函數h（·）表示為

仿真中雷達掃描周期T＝2s，仿真跟蹤步數60步，目標彈道系數β＝40000kg／ms2，蒙特卡洛仿真次數為1000次，目標初始狀態［332000m，2290cos（190°）m／s，98000m，2290sin（190°）m／s］，高斯噪聲環境下觀測噪聲的標準差分別是σr＝100m 和σε＝0．05rad，過程噪聲方差q＝2。

在高斯噪聲條件和閃爍噪聲條件下，分別使用EKF、UKF及PF進行濾波，通過比較不同方向上位置、速度的估計精度和運算時間來對比三種算法的基本性能。EKF采用坐標變換的方法減弱觀測方程的非線性特性，使用一階近似，PF 中粒子數為500，采用殘差重采樣方法。

4．2 仿真結果及分析

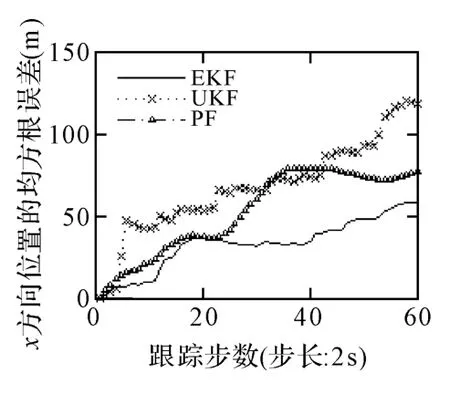
圖1 三種算法在X 軸上位置的RMSE

圖2 三種算法在X 軸上速度的RMSE

圖3 三種算法在Y 軸上位置的RMSE

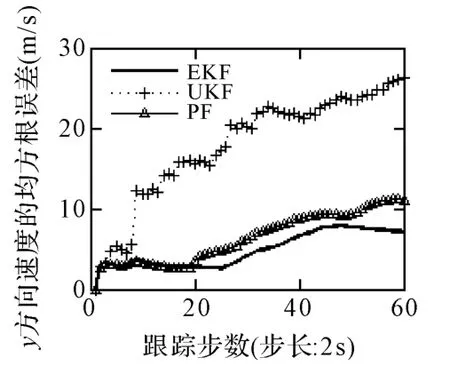
圖4 三種算法在Y 軸上速度的RMSE

圖1比較了高斯條件下三種濾波算法在X和Y軸方向上位置與速度的均方根誤差（RMSE），由于各濾波器的初值已給定，從初始時刻開始三種濾波器就能得到良好的跟蹤效果。圖1中，EKF 和PF對X軸方向上位置變量的跟蹤精度幾乎一致，要略優于UKF。從理論上講，如果適當增加PF的粒子數量和嘗試不同的重采樣算法，會提高其跟蹤精度，但是會帶來運算量的劇增。在仿真的第60步，三種濾波器的結果趨于穩定狀態，分別收斂于60m、70m 和120m 的誤差水平。圖2表明，EKF和PF對X方向上速度估計的性能要優于UKF，誤差僅是后者的1／3左右。圖3中盡管UKF在第40步左右出現190m 的誤差，但是三種濾波器在第50步后，誤差穩定于160m，可以認為三種濾波器的性能相當。圖4可以得到和圖2基本相同的結論。

通過對仿真結果的分析可看出PF 由于在粒子數量和重采樣方法選擇策略兩個條件限制下，并未能達到理想的跟蹤精度，但仍體現出良好的性能，基本與EKF 的性能相當。相同條件的仿真中EKF則要優于UKF，這并非與文獻［10］的論述相悖，只是由于在彈道再入目標軌跡跟蹤問題上，若彈道系數預先確知，對觀測方程采用適當的偽線性變換，削弱其非線性程度，EKF 是可以達到了較為精確的濾波效果的。理論上講，UKF 能夠得到比EKF更高的近似精度，而并非在任何情形下都要優于EKF。UT 作為一種線性化的技術，只是為了獲得濾波器狀態更新時必要的信息，而并不能完全取代其它的線性化技術。

表1給出了MATLAB 中測量的三種濾波器相對于EKF在一次蒙特卡洛仿真中的運算時間。

表1 三種算法的相對運行時間

三種濾波算法中，UKF的運算時間為EKF 的1．85 倍，運行時間與EKF 相當，估計精度不及EKF。PF盡管在運行精度上和EKF相當，運行時間卻是其91．05倍。

表2比較了閃爍噪聲環境下三種濾波算法的X 和Y 軸方向上位置和速度的均方根誤差的均值（ARMSE）。閃爍噪聲采用高斯噪聲和具有“厚尾”特性的拉普拉斯分布噪聲加權和來實現。在嚴重閃爍噪聲干擾條件下，仿真程序中閃爍噪聲權重Weight＝0．9。

表2中，閃爍噪聲條件下EKF 出現了極大偏差，UKF發散，濾波器無法正常工作，因此基于點的濾波器在此條件下失去了對目標的跟蹤性能。PF的ARMSE盡管相對于高斯環境下略有升高，但仍然收斂。

表2 三種算法在閃爍噪聲環境下的ARMSE

5 結語

本文基于彈道再入目標的軌跡跟蹤問題，比較了EKF、UKF 和PF 的性能。通過分析LMMSE濾波器的基本原理，可知所有基于點的濾波算法在狀態更新階段的本質是相同的，僅在線性化策略上有所區別。盡管在高斯噪聲條件下非線性濾波問題中，UKF要比EKF 具有更高階的信息，其性能優于EKF，但在彈道再入目標軌跡跟蹤問題中，如果目標的彈道系數確知，EKF 具有更高的估計精度和更短的運算時間，能夠接近優化后的PF 算法的性能。因此高斯條件下在濾波器的選擇上本文更傾向于EKF 算法。閃爍噪聲條件下，基于高斯假設的基于點的濾波算法失去了理論基礎，濾波器性能出現偏差甚至是發散，此時基于密度的PF 算法就成為了“最優”的估計器，同時對彈道再入目標滯空時間短暫與PF 算法運算時間長的矛盾應該予以重視。

應當指出的是，初始狀態對非線性濾波器的穩定性非常關鍵，彈道再入目標的初始狀態的確定方法對濾波算法的性能會產生很大影響，這個問題有待進一步研究。當彈道系數作為狀態變量的一個待估參量時，其建模方法對非線性濾波器的性能會產生影響。下一步將繼續研究這些因素對彈道目標軌跡跟蹤問題中非線性濾波器選擇策略的影響。

［1］Farina A，Ristic B，Benvenuti D．Tracking a Ballistic Target：Comparison of Several Nonlinear Filters［J］．IEEE Transactions on Aerospace and Electronic Systems，2002，38（3）：854-867．

［2］江曉東，謝京穩，郭軍海．三種非線性濾波在再入彈道估計中的分析研究［J］．戰術導彈技術，2012（1）：43-49．

［3］劉鑫，郭云飛，薛安克．幾種濾波器跟蹤性能的比較［J］．計算機與數字工程，2013（3）：391-393．

［4］Zhao Z L，Chen H M，Chen G S，et al．Comparison of Several Ballistic Target Tracking Filters［M］．New York：IEEE，2006：2197-2202．

［5］Zhao Z L，Li X R，Jilkov V P．Best Linear Unbiased Filtering with Nonlinear Measurements forTarget Tracking［J］．Aerospace and Electronic Systems，IEEE Transactions on，2004，40（4）：1324-1336．

［6］Li X R，Jilkov V P．A Survey of Maneuvering Target Tracking：Approximation Techniques for Nonlinear Filtering［C］／／Pefense and Security．Intemational Society for Optics and Photonics，2004：537-550．

［7］Li X R，Jilkov V P．A Survey of Maneuvering Target Tracking—PartⅢ：Measurement Models［C］／／Internation Symposium on Optical Science and Technology．International Society for Optics and Photonics，2001：423-446．

［8］Yaakov B S，Li X R．Estimation with Applications to Tracking and Navigation：Theory Algorithms and Software［M］．New York：John Wiley ＆Sons，Inc．，2001．

［9］Julier S J，Uhlmann J K．Unscented Filtering and Non-linear Estimation［J］．Proceedings of the IEEE，2004，92（3）：401-422．

［10］Julier S J，Uhlmann J K，Whyte H F．A New Method for the Nonlinear Transformation of Means and Covariances inFilters and Estimators［J］．Automatic Control，IEEE Transactions on，2000，45（3）：477-482．

［11］Gordon N J，Salmond D J，Smith A F M．Novel Approach to Nonlinear／non-Gaussian BayesianState Estimation［J］．Iee Proceedings F Radar and Signal Processing，1993，140（2）：107-113．

［12］Doucet A，Freitas N，Gordon N．Sequential Monte Carlo Methods in Practice［M］．New York：Springer-Verlag，2001．

［13］馮馳，王萌，汲清波．粒子濾波器重采樣算法的分析與比較［J］．系統仿真學報，2009（4）：1101-1105．

［14］Li X R，Jilkov V P．A Survey of Maneuvering Target Tracking-partⅡ：Ballistic Target Models［C］／／Proceedings of 2001SPIE Conference on Signal and Data Processing of Small Targets，2001，4473：559-581．

［15］Ristic B，Farina A，Benvenuti D．Tracking a Ballistic Object on Reentry：Performance Bounds and Comparison of NonlinearFilters［C］／／Radar，Sonar and Navigatio，IEE Proceedings，2003，150（2）：65-70．