基于S函數實現的參數自整定模糊PID控制器

魯改鳳，盧東偉，孟 波，王 佳，鞠 陽

(華北水利水電大學，河南 鄭州450045)

自計算機進入控制領域以來，尤其是數字計算機取代模擬計算機調節器成為計算機控制系統的主要部分以來，不僅實現了軟件的PID 控制算法，而且可以采用計算機本身自有的邏輯功能，使數字PID控制技術的應用更加靈活，更加有實用價值. 數字PID 控制技術是日常生產過程中比較普遍采用的一種基本的控制算法，其控制系統在機電、冶金、機械、化工等行業中獲得了廣泛的應用. 數字式計算機技術結合先進的智能控制理論，二者的綜合發展為復雜動態不確定系統的控制提供了一種新的解決途徑.利用先進的數字智能控制技術，不僅可以設計出先進的智能PID 控制，而且可以對PID 的參數進行智能整定.自整定的模糊PID 參數控制系統能在控制過程中對不確定的條件、參數、延遲和干擾等因素進行在線的檢測后進行確定性的分析，采用模糊推理的方法實現PID 參數KP，KI和KD的在線自整定.此方法不僅保持了一般PID 控制系統對PID 控制參數調節簡單、使用方便、魯棒性強等優點，而且具有比較大的調節靈活性以及適應性，對控制系統中各參數的控制精度比較好，是目前較常采用的一種比較先進的控制系統.

利用MATLAB 方法對模糊自整定的PID 控制系統的參數進行數字仿真，可快速方便地實現多種控制規則，控制參數精度高，使模糊自整定的PID 控制系統的參數控制效率以及準確性得到大大提高［1］.

1 參數自整定模糊PID 控制系統的結構設計

1.1 參數自整定模糊PID 控制系統的結構

參數自整定模糊PID 控制系統的結構主要由2部分組成:一是參數可變的PID 控制器，二是模糊控制系統.其結構如圖1所示.

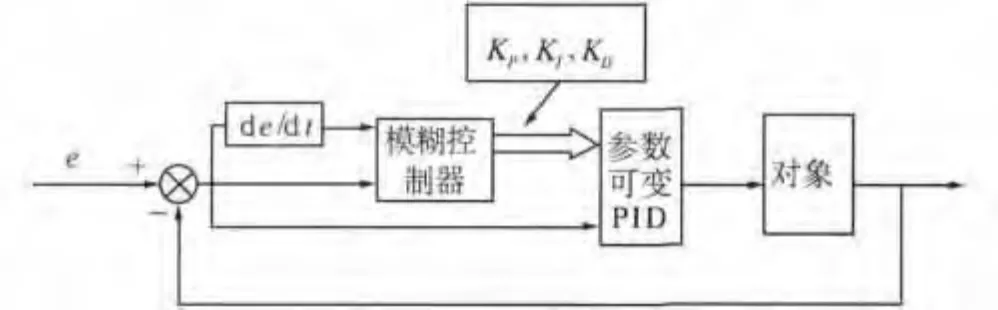
圖1 自整定模糊PID 參數控制系統框圖

誤差e 和誤差的變化率de/dt 送入模糊控制器，經過模糊化及模糊運算，得到輸出的模糊控制變量，再通過解模糊，得到PID 控制器的3 個控制參數KP，KI，KD，這3 個參數再輸入到PID 控制器中，然后再應用于控制對象.

應用模糊集合理論建立控制器參數KP，KI，KD與系統誤差絕對值e 和誤差變化率絕對值de/dt 之間的二元連續函數關系，通過模糊控制器根據不同的e 和de/dt 在線自整定來確定PID 的3 個參數.以滿足不同e 和de/dt 對控制參數的不同要求，從而使被控對象達到良好的性能要求.

1.2 PID 參數整定原則

常規PID 控制算法的離散形式為［3］:

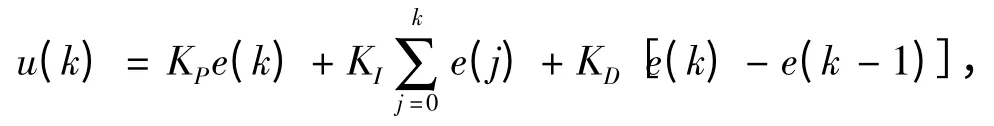
式中:k 為采樣序號，k = 1，2，…;u(k)為第k 次采樣時刻控制器的輸出值;e(k)為第k 次采樣時刻的輸入偏差值;e(k－1)為第k－1 次采樣時刻的輸入偏差值;KI為積分系數，KI= KPT/TI;KD為微分系數，KD= KPTD/T.

1)當e 的絕對值較大時，若使PID 控制系統具有較良好的跟蹤性能，這時取較大的KP，以及較小的KD，同時為避免控制系統響應出現超調大，這時應對積分的控制作用加以限制，通常取KI= 0.

2)當e 的絕對值處于中間大小時，為使控制系統響應超調較小，此時KP的值應取較小值. 在此種情形下，控制系統中KD的值響應較大，KI的取值應適當.

3)當e 的絕對值較小時，為了使當前控制系統有比較良好的穩定性，KP和KI均應取大值，同時為避免控制系統在預先設定的初值附近出現比較大的振蕩，當de/dt 值較大時KD取較小值，通常KD為中等大小.

1.3 各變量在模糊控制器中隸屬度函數的確定

由PID 控制系統參數的在線自整定原則可以確定e，de/dt，KP，KI，KD的隸屬度函數.PID 參數控制的模糊控制器的輸入是2 輸入，而輸出為3 輸出.在控制器中以e 的絕對值和de/dt 的絕對值為輸入參數變量，以KP，KI，KD為輸出參數變量. 模糊控制器的各個參數變量的基本論域為誤差絕對值e = {0，E1，E2，E3}.誤差變化率絕對值

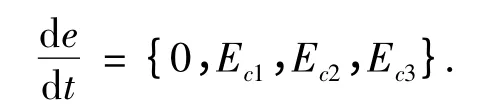
輸出KP= {0，UP1，UP2，UP3};

輸出KI= {0，UI1，UI2，UI3};

輸出KD= {0，UD1，UD2，UD3}.

變量e，de/dt 和KP，KI，KD的論域取值大(B)，中(M)，小(S)，零(Z)，其中Z 采用zmf 隸屬度函數，B 采用smf 隸屬度函數，S，M 則采用trimf 隸屬度函數［4］.

誤差比例系數和誤差變化率比例系數對模糊控制器的影響也很重要［5］.若誤差的基本論域為［－e，e］，誤差變化率的基本論域為［－ ec，ec］，誤差模糊狀態的基本論域為［－ n，n］，誤差變化率的模糊狀態的基本論域為［－ m，m］，則誤差比例系數Ce和誤差變化比例系數Cec可由下列公式決定:

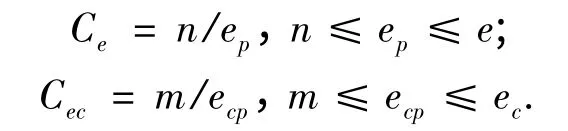
參數可變PID 控制器的結構如圖2所示.

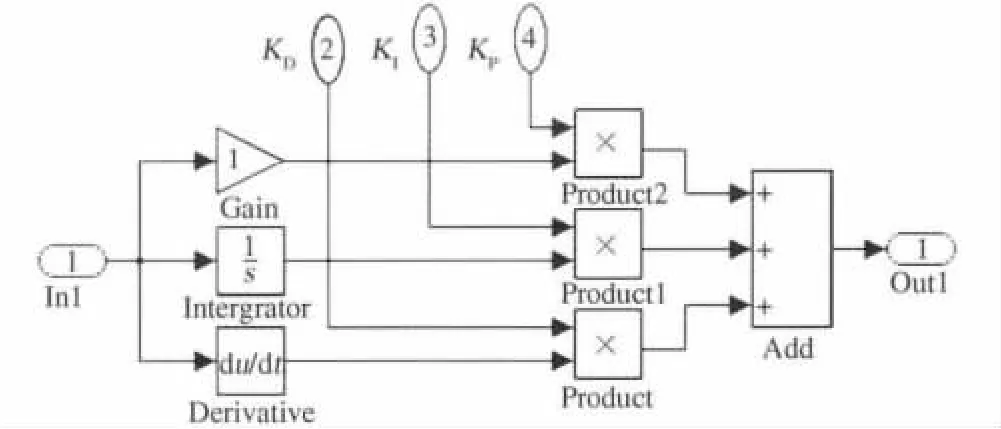
圖2 參數可變PID 控制器結構圖

2 大時間延遲系統的參數自整定模糊PID 控制仿真

該次仿真的大時間延遲系統的數學模型為exp(－200 s)×3/(7 000 s +1)，該系統為帶有純滯后的一階慣性環節.

先在MATLAB 中利用次最優降階法對該系統進行近似，然后再用Ziegler－Nichols［6］經驗公式得到PID 的3 個相關參數KP，KI和KD，即KP=0.485 1，KI= KP/ti= 0.242 5，KD= KPtd= 2.425，然后利用此3 參數構成的連續PID 控制器對exp(－200 s)×3/(7 000 s + 1)這一對象仿真. 經過多次仿真發現KP，KI，KD這3 個參數分別整定在14，0.001，1 600時，系統的性能比較好. 其實現過程有如下3 種:①設定誤差的模糊狀態的基本論域為［0，10］，設定誤差變化率的模糊狀態的基本論域為［－ 3，3］;②設定誤差的模糊狀態的基本論域為［0，3］，設定誤差的模糊狀態的基本論域為［0，0.003］;③設定誤差的模糊狀態的基本論域為［0，300］，設定誤差的模糊狀態的基本論域為［0，0.000 03］.

設定在3 個不同的基本論域并反復調試，假設Ce= 1/50，Cec= 5，KP的作用因子為2，KI的作用因子為1，KD的作用因子為2，然后根據參數整定原則寫出模糊控制規則表.

同時為了縮短系統響應時間，在e ＞200 時采用PD 控制，使KI= 0，在e ≤200 時模糊控制器的輸出才起作用.

2.1 利用S 函數構建模糊控制器的方法

交互式的模型輸入與仿真環境SIMULINK 工具箱是MATLAB 仿真軟件的擴展，是一個用來對動態系統進行建模、仿真和分析的軟件包，其中S 函數(S-Function)是SIMULINK 提供的內置模塊，是SIMULINK 模塊的計算機語言描述，用戶可以在S函數中編程實現算法.

在利用S 函數構建模糊控制器的過程中，要用Flag = 0，Flag = 2，Flag = 3 這3 種情況.其中Flag =0，調用初始化函數，對該S 函數進行初始化;Flag =2，調用離散狀態的更新函數，模糊規則表的建立，各種模糊控制量的建立，都是在該離散狀態的更新函數中完成;Flag = 3，輸出解模糊后的KP，KI和KD.

2.2 利用S 函數構建模糊控制器的過程

模糊控制器為2 輸入和3 輸出的模型，誤差e，和誤差變化率de/dt，作為輸入，KP，KI，KD為輸出，e，de/dt，KP，KI，KD的模糊子集均為{B，M，S，Z，S，M，B}，其編寫的S 函數如下.

編寫完畢后，將其存盤為fpids.m 文件(文件名和函數名應一致)，以備在SIMULINK 庫中，即SFunction 塊調用.

2.3 仿真結果

MATLAB 仿真軟件建立起系統模型如圖3所示，用S 函數模塊對PID 參數進行模糊處理，通過多次修改控制規則進行優化設計，并經反復調試確定最終參數［7－9］.

通過仿真可以發現，該系統在設定為1 000 時的上升時間為1 250 s 左右，超調不超過1.8%，調節時間小于2 000 s，如圖4所示. 同時，在同樣的PID 控制器中如果不加模糊控制器，可以發現當加入干擾后普通的PID 控制系統需要更長的調節時間，并且超調量更大.

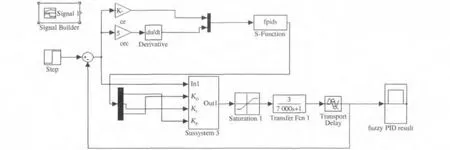
圖3 基于S 函數模糊整定－PID 控制器系統仿真結構圖

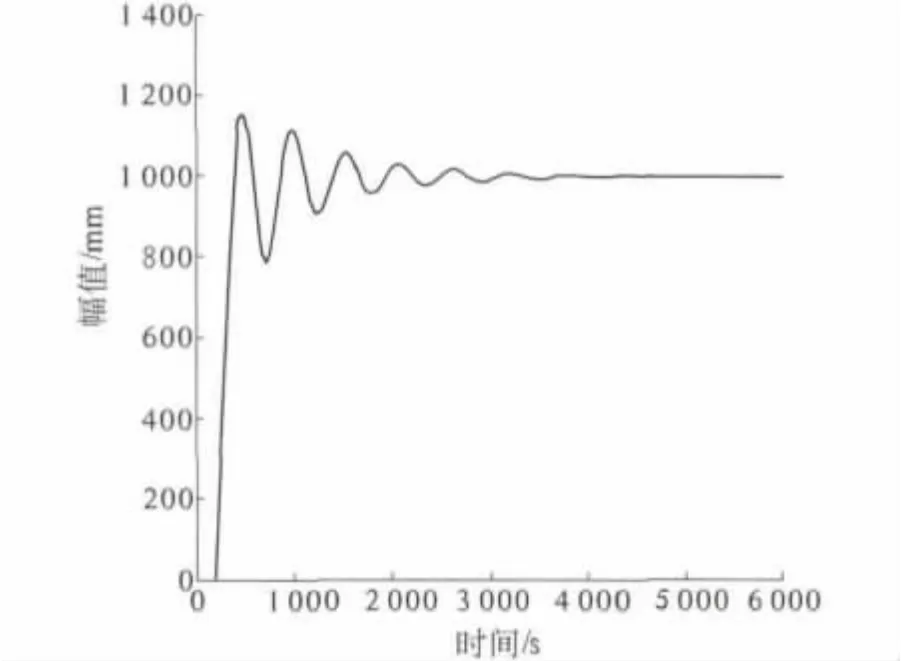
圖4 模糊PID 控制的階躍響應

3 結 語

采用參數自整定模糊PID 控制系統，對于上述的大時間延遲系統來說，它的響應時間更短，超調量小，系統的魯棒性也有很大的改善.文中提出的利用S 函數實現模糊整定PID 控制器的方法，對于隧道窯溫度控制、水溫控制的大時間延遲系統的控制性能改善有較大的實際意義.

［1］黃曉宇.基于MATLAB 的模糊自整定PID 參數控制器的計算機仿真［J］.自動化與儀器儀表，2001，95(3):21－24.

［2］吳振順，姚建均.模糊自整定PID 控制器的設計及其應用［J］.哈爾濱工業大學學報，2004，36(11):576－580.

［3］孫庚山，蘭西柱.工程模糊可能改制［M］.北京:機械工業出版社，1995.

［4］王鳴.基于模糊控制理論的一種PID 參數自整定控制的設計和仿真［J］.自動化與儀器儀表，2000，87(1):14－17.

［5］王耀南.計算智能信息處理技術及其應用［M］. 長沙:湖南大學出版社，1999.

［6］劉金琨.先進PID 控制MATLAB 仿真［M］.北京:電子工業出版社，2004.

［7］費春國.模糊自調整控制器的研究及應用［D］.天津:天津科技大學，2003:25－26.

［8］楊智.工業自整定PID 調節器關鍵技術綜述［J］. 化工自動化及儀表，2000，27(2):5－10.

［9］李卓.基于模糊推理的自整定PID 控制器［J］.控制理論與應用，1997，14(2):238－243.