通用強度折減點安全系數的定義及在邊坡穩定分析中的應用

□王 佳（山西省水利建設開發中心）

0 引言

點安全系數是衡量結構安全度的重要指標，其計算方法主要有傳統安全系數法、超載法、傳統強度折減法。傳統強度折減法的定義為保持作用在模型上的荷載大小與分布不變，按一定的方式逐漸降低材料強度參數值，直到模型破壞。傳統強度折減點安全系數即是材料的設計強度參數和模型破壞時的材料強度參數的比值，該參數反映了材料每一點的強度儲備。但是該安全系數有非常大的局限性。首先，對于某些準則，例如mohr-coulomb準則來說，傳統強度折減系數有取值上的局限性——必須在一定的取值范圍內才能使該方法有意義。另外，對于在確定拉壓比情況下的多參數準則，不同的參數折減會造成此系數的不同結果，影響結構安全度的判斷[1]。因此，定義一個不受上述限制的通用的強度折減安全系數是非常必要的。

1 基于通用強度折減法的點安全系數

1.1 通用強度折減點安全系數的定義

對于各向同性材料，材料的破壞面或強度極限面在主應力空間一般表示

或用應力不變量表達[2]如式

或用Haigh-Westergaard坐標系[3]表示為：

其中：

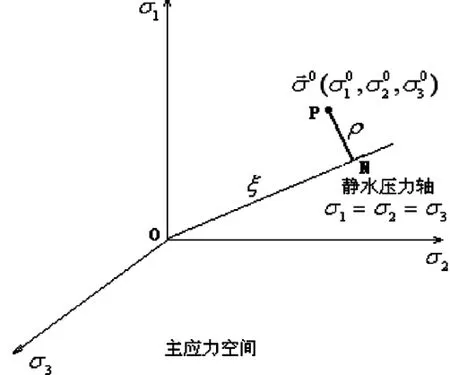
圖1 主應力空間中應力狀態的幾何表示圖

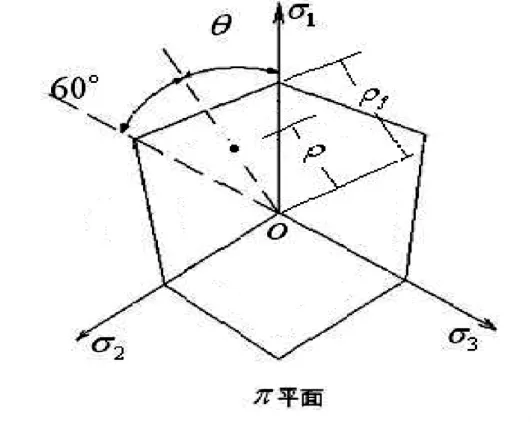
圖2 極半徑與臨界極半徑示意圖

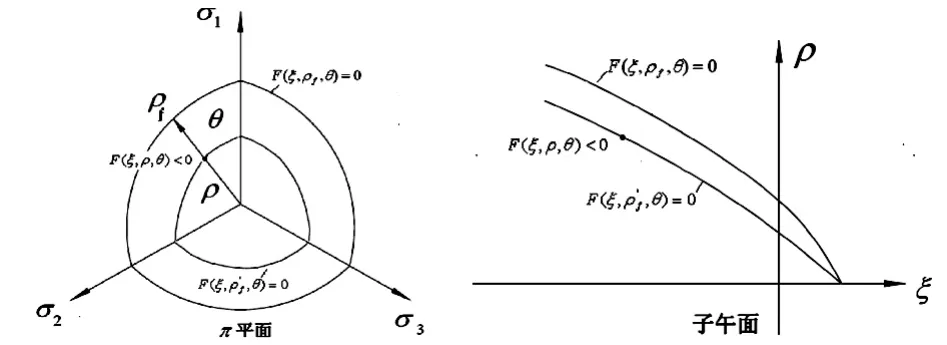
圖3 通用強度折減法的物理意義圖

通用強度折減法也是基于強度折減的思想，不同的是，其物理意義不是指強度參數的折減，而是通過π平面臨界上極半徑ρf的擴大或縮小，使強度極限面整體擴大或縮小，最終使得應力點落在強度極限面上，即達到強度極限狀態，如圖3所示。由此，定義新的安全系數——通用強度折減安全系數表達式為：

根據定義，可以得到新定義的安全系數滿足以下條件：

圖4 通用強度折減安全系數計算示意圖

1.2 通用強度折減點安全系數計算

如上節所示，通用強度折減點安全系數為應力點相應的臨界極半徑與該點極半徑的比值。臨界極半徑的求解如圖5，以Mohr-Coulomb準則為例，E點為應力點D到強度極限面最短距離的點，也稱為失效點。DE為應力點D的失效距離[3]。從圖4中可以看出DE⊥AC，且△ABC≌△DEF≌△EFC，根據相似關系，可以得到

其中：

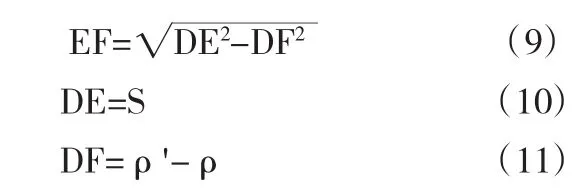
從而可以得出：

當準則的強度極限面為曲線時，求解時可以用曲線的割線距離來計算。因此可以得到該應力點的通用強度折減安全系數：

通用強度折減系數的幾何意義就是調整強度極限面F(ξ,ρf,θ)＞0，使其極半徑除以一個系數 Kf，從而使應力點（σ1，σ2，σ3）落在新的假設強度極限面F(ξ,ρf/Kf,θ)=0上。換言之，也即是保持其ξ,ρ,θ，也就是其應力狀態不變，調整應力點σ1，σ2，σ3）的半徑乘以一個系數Kf，使其落在強度極限面上，得到 F(ξ,ρ·Kf,θ)=0，以 Mohr-Coulomb 準則為例，如圖 5所示。

圖5 通用強度折減法的幾何意義圖

2 通用強度折減安全系數在水利工程中的應用

安全系數在水利工程中有大量應用，經常見于堤防邊坡、大壩邊坡及巖洞的穩定計算。此處以某河流堤防工程邊坡穩定分析為例，通過有限元建模計算，分析比較通用強度折減安全系數與傳統邊坡穩定安全系數的計算成果。

2.1 工程概況

某河流邊坡堤防工程全長3.52 km。該工程右岸堤防樁號0+700～3+515段按河堤標準進行護砌，采用斜坡式和直斜復合式斷面，堤頂寬12.00 m，堤頂高程5.10～5.70 m。根據景觀總體布局，堤頂高程5.10～高程3.50 m、高程3.50 m～高程2.50 m分別采用三維植被網、干砌方塊石和直擋墻護砌，并適當布置景觀臺階和觀光平臺，高程2.50 m～坡腳（設計河底高程）采用干砌方塊石護坡，高程3.50，2.50 m處設消浪平臺寬3.00m，堤基采用大開挖置換處理，堤身回填開山石渣。右岸堤防樁號2+220斷面圖如圖6所示。

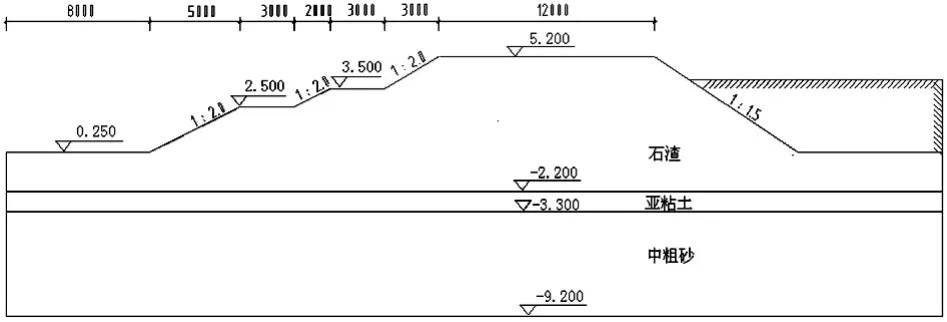
圖6 某河流右岸堤防樁號2+220斷面圖

2.2 材料參數及計算工況

2.2.1 設計斷面和材料參數

該河右岸堤防工程的設計斷面如圖6所示，各土層材料參數列入表1。

點強度參數折減法下和通用強度折減法下的土坡安全系數均可以較好地反映土坡的穩定性。根據《堤防工程設計規范》，對于3級建筑物，正常運用條件下，采用瑞典條分法計算的壩坡抗滑穩定安全系數≥1.20，非常運用條件的安全系數應≥1.10，由表2可知，各計算斷面在各工況下的邊坡穩定安全系數均大于規范要求值，滿足穩定要求。工況2的安全系數小于工況1的安全系數，與前面位移分析時的預測相符。

從表中數據可以看出，點強度參數折減法下的土坡安全系數在情況1時，與瑞典條分法接近；在情況2時大于后者，約3%～6%。通用強度折減法下的土坡安全系數普遍小于強度參數折減法：在情況1時，也小于瑞典條分法下的安全系數，約5%～7%；情況2的土坡安全系數與瑞典條分法下的安全系數接近。由此可見，點強度參數折減法下的土坡安全系數在一定程度上雖然可以作為土坡穩定分析的代表值，但若從計算角度來看，它大于極限平衡法的上限值，從工程角度來看則偏于危險。而通用強度折減法下的土坡安全系數同樣可以作為實際工程的代表值，從計算角度更為合理，從工程角度則更為安全。

表1 樁號2+220堤防斷面壩基各土層物理參數統計表

2.2.2 計算工況和荷載情況

根據《堤防工程設計規范》（GB50286-98），該工程的地震設計烈度為6度，不進行抗震計算。由于該河設計洪水位比規劃地面低，故僅對堤防臨水側邊坡進行抗滑穩定計算，計算工況選取施工期、100年一遇設計洪水位3.84 m兩種工況進行計算。

土坡的荷載情況為：兩個設計工況均有重力荷載和堤頂荷載。運行期在浸潤線下采用浮容重，不考慮臨水側水壓力荷載。堤頂路段兩側是人群荷載，均布4 kPa，分布寬度每側2.50 m。中間是汽車荷載，荷載值22.321 kPa，分布寬度7 m。不計地震荷載。

2.3 有限元計算結果分析

該模型是非均質成層多級土坡，采用單元形心處的主應力計算。因土坡為成層多級土坡，破壞型式為兩次破壞過程，分別為第一級土坡破壞和整體土坡破壞。為了更好地直觀計算結果，在此稱第一級土坡破壞為情況1，土坡整體破壞為情況2。分別記錄兩個情況下的折減系數，列于表2。剛體極限平衡法的結果運用北京理正軟件進行瑞典條分法下的邊坡穩定安全系數，連同規范允許值一并列入表2。

表2 臨水側邊坡穩定安全系數表

3 結語

基于臨界極半徑折減的的通用強度折減法對傳統強度折減點安全系數的局限性進行改進，具有明確的物理意義和幾何意義，且符合強度安全的度量方式。通過對巖土材料和混凝土材料的多種強度準則計算，文章定義的通用強度折減點安全系數能夠正確地反映各種應力條件下的點安全度，具有良好的表征性。文章定義的強度折減點安全系數具有實用性，該邊坡工程作為非均質成層多級土坡，是一個典型的人工復雜土坡。對于這樣的實際工程，通用強度折減法仍然可以較好地反映土坡的穩定性，具有實際應用意義。

[1]錢向東，焦彩虹.基于多參數強度準則的安全系數定義問題[J].水利水電科技進展,2007,27(4)：34-37.

[2]陳惠發，A.F.薩里普.混凝土和土的本構方程[M].北京：中國建筑工業出版社，2004.

[3]錢向東，姜弘道.多軸強度安全系數的定義及應用[J].建筑科學與工程學報,2008,(1)：37-42.