由劣弧測量而引出的一種新的描述及評價測量的方法
平夏PING Xia;王國民WANG Guo-min;童云飛TONG Yun-fei
(無錫市計量測試中心,無錫 214101)
(Wuxi Measurement Test Center,Wuxi 214101,China)
0 引言
首先,要指出一個長久以來存在的誤區。我們總是會看到這么一句話:“一直以來,劣弧的圓心及其半徑的測定是一項未解決的技術難題……”其實,這并不是一個真實存在的很嚴重的問題。當然,這里并不是說能夠測準劣弧圓心和半徑,事實上確實是測不準,但是,為題在于:我們為什么一定要測準圓心和半徑?這么做有何實際意義?
事實上,真實存在的點處于弧狀部位,我們實際測量的正是這些點的位置,而所謂用各種方法擬合出來的圓心和半徑只是我們自己定義的一個假象的概念,它們的重要性是很低的。那么如何來描述及評價一段劣弧,是本文將要探討的問題。
1 描述與評價
在幾何量測量中,永遠是取實際物體的某些特征點,即使是掃描也不可能“面面俱到”,所以測量的點的數目是可數的。某次測量了若干個點,我們稱記錄測量點的過程稱之為“描述”。
在測量完畢后,我們要把記錄的數據進行處理以得到測量的結果,那么我們稱處理數據的過程為“評價”,那么將上述N 個點擬合成的圓、平面、直線等就是評價的結果。
2 傳統的描述與評價
三點擬合圓的方法是大家都熟知的,那么在零件表面的形狀誤差與測量誤差不可避免的情況下,所采點的誤差與所計算出來的半徑誤差存在如下關系:
如圖1,設實際測得到三點A1,B1,C1與理論三點A,B,C 的誤差均為e,可以推導得:
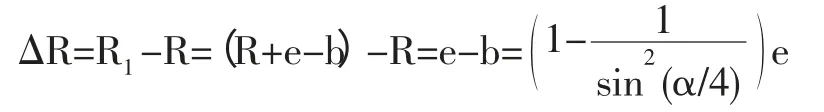
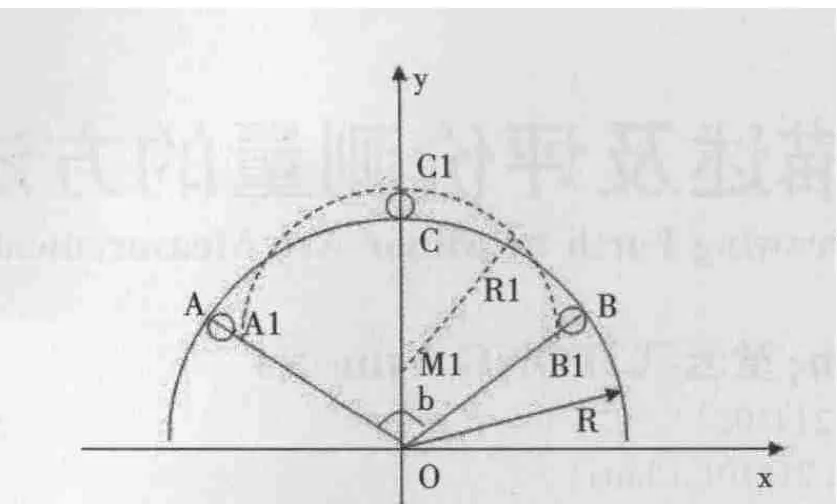
圖1
由上式可知,圓心角越小,誤差放大比例越大,這就是所謂的“差之毫厘,謬以千里”。
那么為什么會引起誤差放大呢?正是因為我們的描述不是一個完備的描述,即使我們在劣弧上盡量采集更多的點,它也是不完備的,那么用傳統的評價方式得到的半徑及圓心坐標偏離理論值就非常大。
通常來說,上述“描述”的“評價”可以取為:
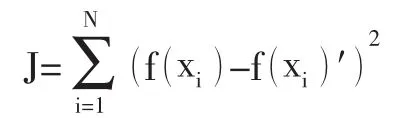
其中f(xi)為實際測量點,是原始的描述,f(xi)′為擬合圓,是評價的結果,J 越小說明越接近實測點的真實信息。最小二乘法的思想就是令J 取最小值為約束條件,從而得到一些結果。
3 一種新的描述與評價
圓與圓弧的測量一般分為二種情況:定圓心與半徑的測量或只定半徑的測量。
對于整圓或大圓心角圓弧來講,測量圓心位置及半徑是較為簡單的問題,這里不作進一步討論,而對于劣弧來說,測量圓心位置及半徑就如引言中所說,是測不準的。那么我們是否能換一種思維方式呢?測不準圓心位置及半徑,我們是否能通過評價其輪廓度來確定其圓心位置及半徑的準確性?我們認為是可行的,與實際工作狀態也是相符的。這就引出了一種新的描述與評價。
以劣弧為例,這種“描述”型式的“評價”怎么計算呢?
我們令f(x)=(x-x0)2+(y-y0)2=R2,該曲線為理論圓的“描述”曲線。
當所測劣弧是定圓心與半徑的,則其描述與評價如下式:J=max
上面表達式的含義是求出每個實測點到理論圓心的距離與理論半徑的差值的絕對值,取其中的最大值為J,則其輪廓度為2J。
當所測劣弧只定半徑,則其描述與評價就相對復雜,如下式:J=
上面表達式的含義如下:不斷平移同一個“描述”曲線(即理論圓),計算每個實測點到理論圓心的距離與理論半徑的差值的絕對值的最大值,這些不同位置的“描述”曲線所得到的所有值中取一個最小值,將此最小值作為我們的“評價”:J,取2J 作為該劣弧的輪廓度。該描述與評價可以編制一應用程序,進行快速計算,部分程序見下:
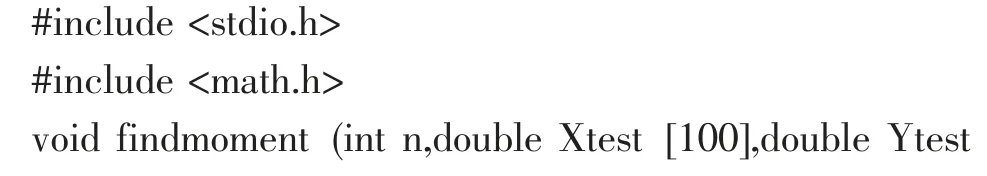

綜上所述,傳統的“描述”是記錄測量點的過程,“評價”是擬合特征(圓、橢圓、面、線)的過程,評價結果為特征,例如由圓心及半徑構成的圓。而我們新的“描述”是先構建理論曲線(特征),然后對測量點與“描述”曲線進行“評價”,評價的結果為一偏離量。
有了這種:“測點——描述——評價”的思想,就可以把長度與幾何量測量中的幾乎所有有關誤差放大的問題歸結于同一類,即:我們只需要關心怎么把每一個單點測量準確,而不需要考慮其他問題,因為那些都可以用“測點——描述——評價”的思想加以解釋,這種方法有邏輯性,并且與工業中的實際操作更為契合。
下面給出一個在會產生誤差放大的測量中如何表示測量結果的建議:
①給出描述類型,比如“圓描述”或者“橢圓描述”等;②給出此描述的“評價”,即J(偏離量)的表達式;③求出此次測量的J 的數值。
4 結論
前面討論了由劣弧測量而引出的一種新的描述及評價測量的方法,主要是為計量檢測人員提供一種新的檢測思路,不能總是按部就班,受困于傳統的思維方式中。希望能與大家共勉,共同提高計量檢測技術。
[1]陳其偉.三坐標測量短圓弧和短直線[J].金屬加工,2002.
[2]第一機械工業部.六項基礎互換性標準匯編[M].中國標準出版社,2004.
[3]董良海.關于短圓弧測量問題探討[C].江蘇省計量測試學會論文集,2010.

