表面貼裝翼形引腳焊點3D外形預測

鄭冠群

（深圳職業技術學院 電子與信息工程學院，廣東 深圳 518055）

表面組裝技術（Surface Mount Technology，SMT）是現代電子產品的主要組裝技術，SMT焊點的特點是微小、密集、種類多，既要保障電氣性能暢通，又要保障機械連接可靠[1]．焊點的外觀形態直接影響焊點的質量，也間接的影響焊點的可靠性[2]，因此精確預測焊點形態非常重要．

1 焊點形成的數學描述

SMT焊點形成過程可簡單描述為在元件與基板間施加焊料，加熱，焊料受熱熔化后沿元件金屬化端和PCB焊盤表面潤濕鋪展，冷凝后形成具有一定幾何外觀形態的焊點．根據熱力學基本理論，任何系統的存在遵循能量最小原理，因此焊點的形態可認為是由液態焊料以及與其接觸的固相、氣相所組成的三相系統能量趨向最小時的，即達到靜態平衡時的焊料的外觀形態．為了簡化問題，建立模擬焊點形成的數學模型，本文對互連軟釬焊焊點的形成過程做了如下假設[3]：（1）焊盤與釬料接觸表面平整，相互之間不會發生滲透；（2）焊料內部不產生孔洞，夾雜等缺陷；（3）在潤濕過程中，焊料不發生氧化等反應，其成分、性能固定；（4）焊料在期間一直處于融化狀態，溫度梯度為零，熱膨脹以及化學勢均導致的體積變化均不考慮．

依據能量最小原理，在不受外力的情況下，整個系統總能量E可以表示為重力勢能Eg與表面勢能Es的之和：

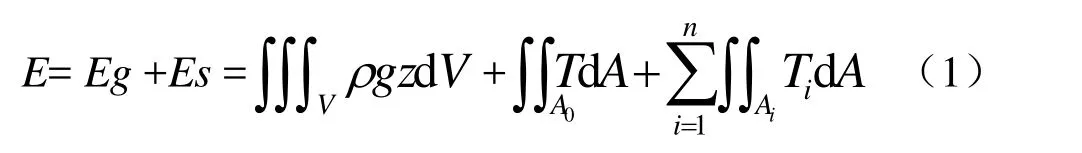
式中，ρ為焊料的密度； g為重力加速度； z為高度，V為焊料的體積；iT為固液界面的張力；T為表面張力； A0為焊料自由表面的面積； A 為固液界面的面積；n為焊料接觸的固相界面的數量．

當系統受外力時，最小能量為：

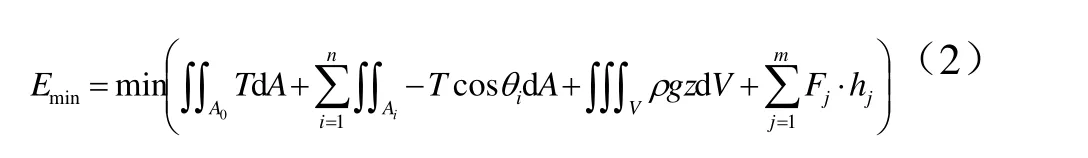
式中，Fj為系統外力； hj為外力作用高度； m為外力總數；iq為焊料與固相接觸角．

2 焊點形態計算的有限元方法

有限元模擬計算的方法一般分為如下3步：

1）整體結構離散化．用有限單元方法模擬計算，首先要將整體結構劃分成有限數量的單元，單元之間通過節點彼此相連接．

2）對于單元的求解．通過對單元進行力學分析建立單元剛度矩陣Ke．對于平面靜力學問題，

應用虛位移原理得到：

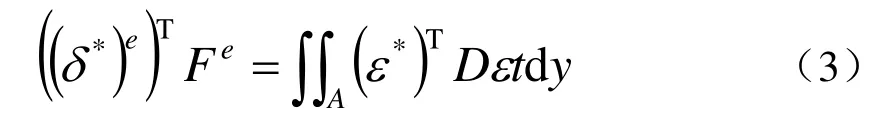
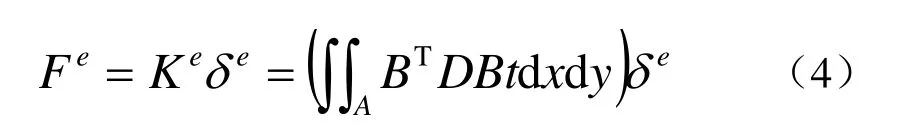
式中，B為應變矩陣; D為彈性矩陣，

對于三節點的三角形單元，為線性位移模式，單元剛度矩陣為

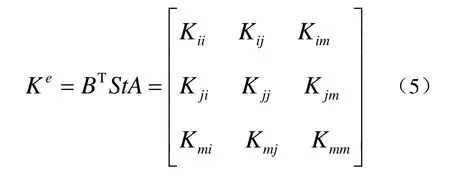
式中，i, j, m為三角形單元節點編碼．

對于平面應力問題有：

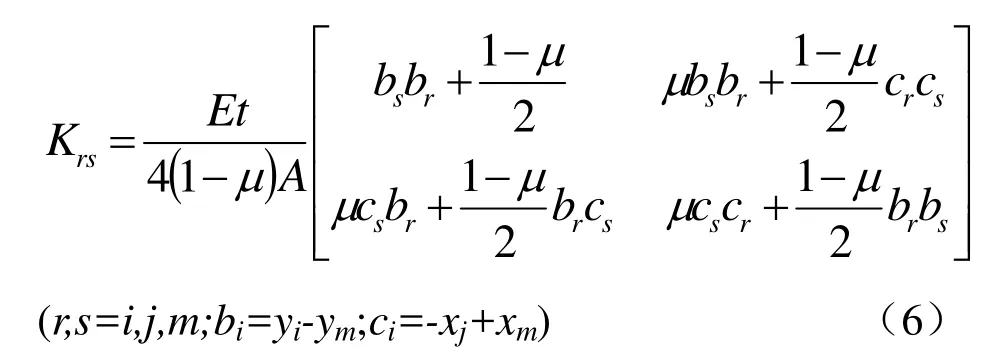
單元抵抗變形的能力可以通過單元剛度矩陣表示，為通過單元所引起的節點力來定義其元素值．其矩陣是對稱矩陣且不可求逆，具有奇異性．

3）整體分析．有限元分析方法在結構分析中只采用節點載荷，單元之間通過節點傳遞力，表面力，體積力與集中力都移動到節點中加載，按照順序形成載荷矢量，并得到總體的平衡方程：

式中，P?等效節點載荷．

最終引進邊界約束條件，求解節點位移．

3 翼形引腳焊點模型

本文所使用釬料為經過熱風重熔的液態Sn-3.0Ag-0.5Cu進行模擬，假設釬料在純 Cu焊盤上進行鋪展，在不潤濕基地上完全不潤濕，所選的基本潤濕鋪展參數見表1．

本文對翼形引腳器件的焊點建立了焊點形態模型，模擬翼形引腳焊點形成的初始形態模型如圖1所示．

如圖2所示，模型中液體焊料體由自由液面F1-F4，引線側面F5，F6，引線豎直端面F7，引線底面F8，引線彎角面F9以及焊盤表面F10圍成．對于引線彎角平面，其能量與體積約束的建立要引入間隙面．當模型中有圓弧或曲面的時候，建模時使用直線來代替弧線，因此在直線外側和弧線之間將存在一個間隙面（gap）．如果不對其進行特殊處理，計算中gap將不斷變大使計算失真．因此必須對gap進行特殊處理，使其也具有相應能量和等效體積描述．gap中的弧線，叫做間隙弧線（gap trace），模擬弧線的直線叫做間隙邊（gap edge）．在處理引線的彎角部分的兩端頭時，我們將引入gap面．

表1 液態Sn-3.0Ag-0.5Cu無鉛焊料基本潤濕鋪展參數[4-5]

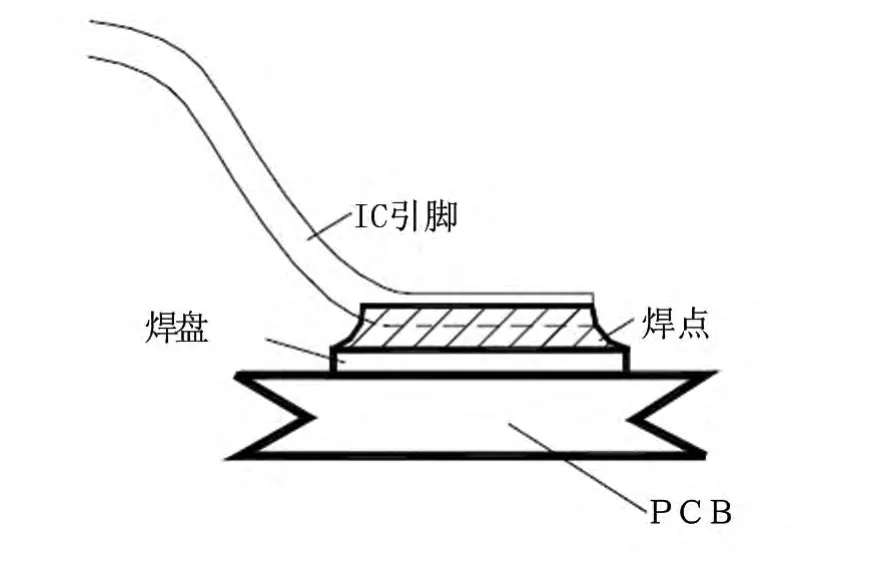
圖1 翼形引腳焊點結構

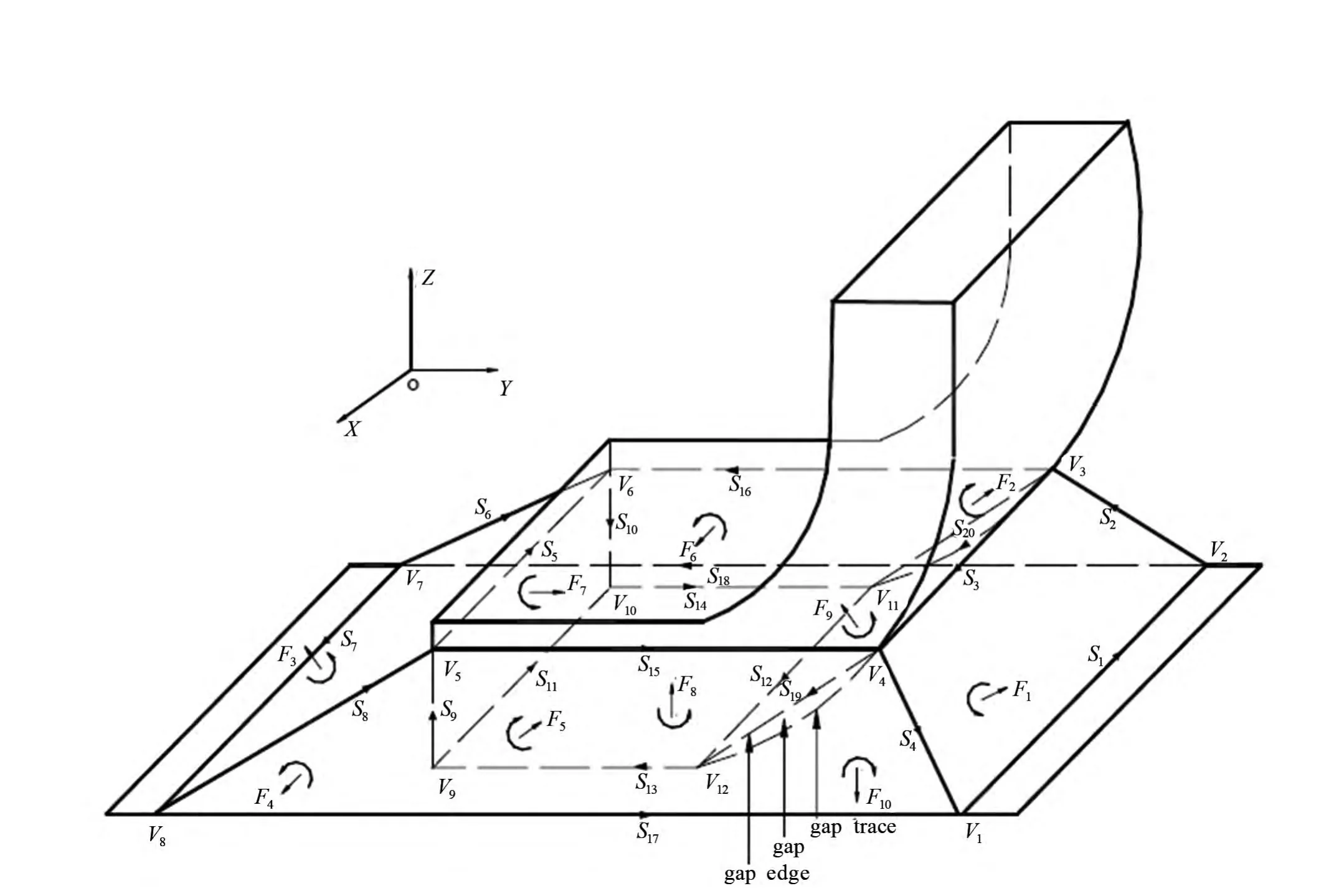
圖2 翼形引腳焊點三維形態模型

1）表面勢能：因假設焊料不能淹沒引線，故引線內側不與焊料接觸，只需考慮引線外側．引線外側的空間約束為表面勢能可描述為：

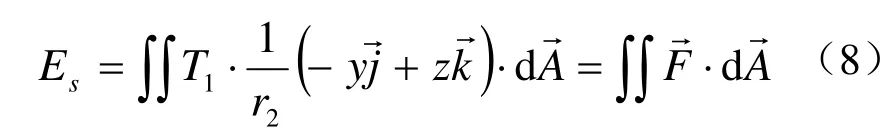
式中，T1為焊料沿引線表面鋪展的界面張力，r2為引線外側圓角半徑．

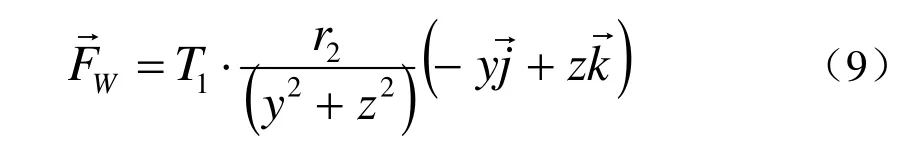
由斯克托司公式可得：

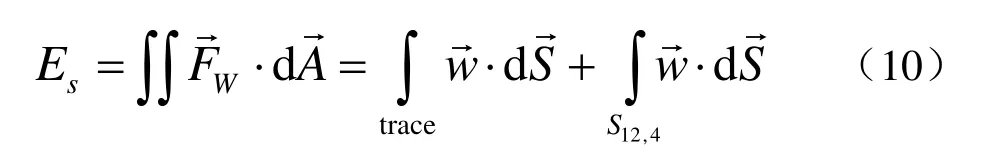
因在實際計算模型中，只有gap edge，gap trace并不存在，因此需要把gap trace上的線積分過渡到gap edge．因 ? ′ 與gap平行，所以

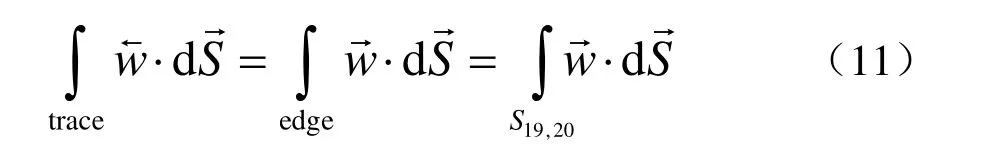
2）重力勢能：可描述為：

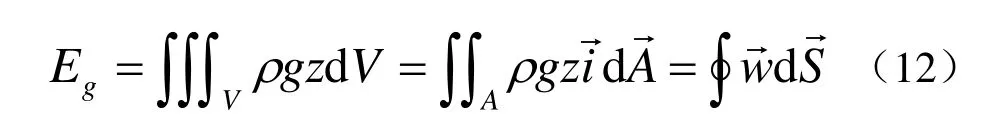
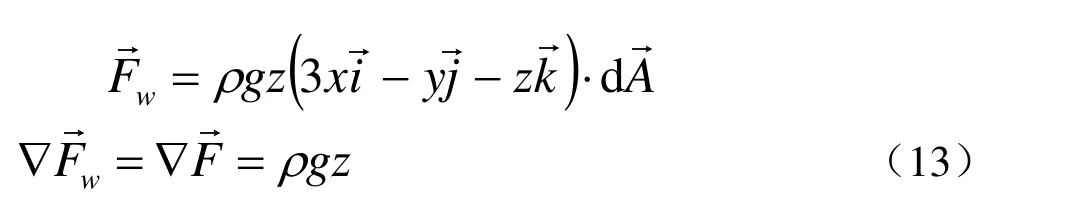
可得：

式12可表示成為：

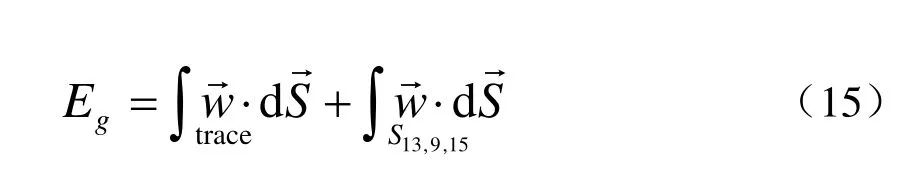
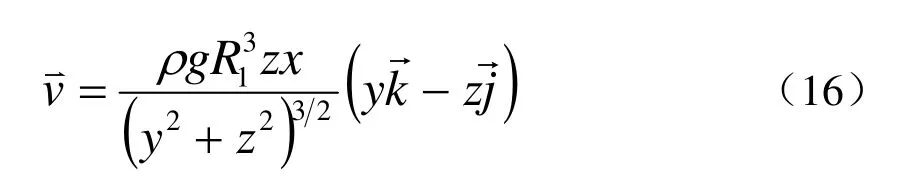
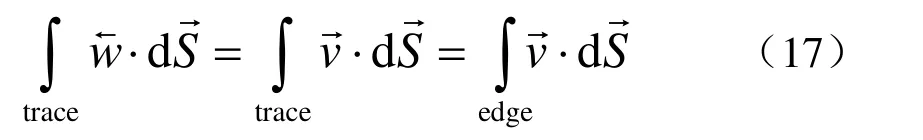
重力約束定義方式為直接把v加到間隙邊的定義中，對于引線另一側面的重力勢能，采取同樣的辦法可以推得．

3）體積約束：對于引線彎角柱面有：

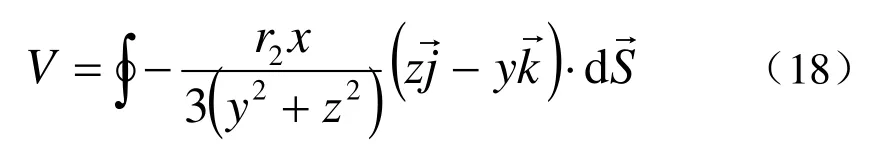
對于引線側面（包括面F5與間隙面gap）有：

定義無散矢量：

則有：

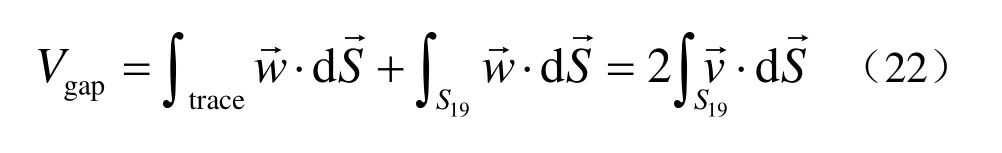
在進行求解的過程中，求解結果與網格劃分有很大關系．為了得到更為精確地答案，需要進行多次迭代．但迭代的過程中，需要把小于一定長度的線刪除，并且把小于一定面積的面刪除后，重新劃分網格并進行迭代計算，這樣才能得到較為精確地結果．以SOP封裝焊點為例，圖3（a）為SOP封裝焊點在不進行刪除重復網格，重新劃分網格的情況下分別迭代多次所得結果，可以看出，在不進行網格清理的情況下，多次迭代不僅沒有令求解結果達到所預期的接近真實的情況，反而使得求解不收斂，最終出錯，當迭代到80次后，結果與實際不吻合．而如果在迭代過程中，不斷刪除重復網格并重新劃分網格，能保證系統能量的最小化，得到的結果與實際吻合，如圖3（b）所示．焊料在Cu焊盤表面進行了鋪展，潤濕面積比初始形狀有所增加，而中間的面積有所減小．與吳玉秀等[6]所得結果相似，證明結果較為合理．

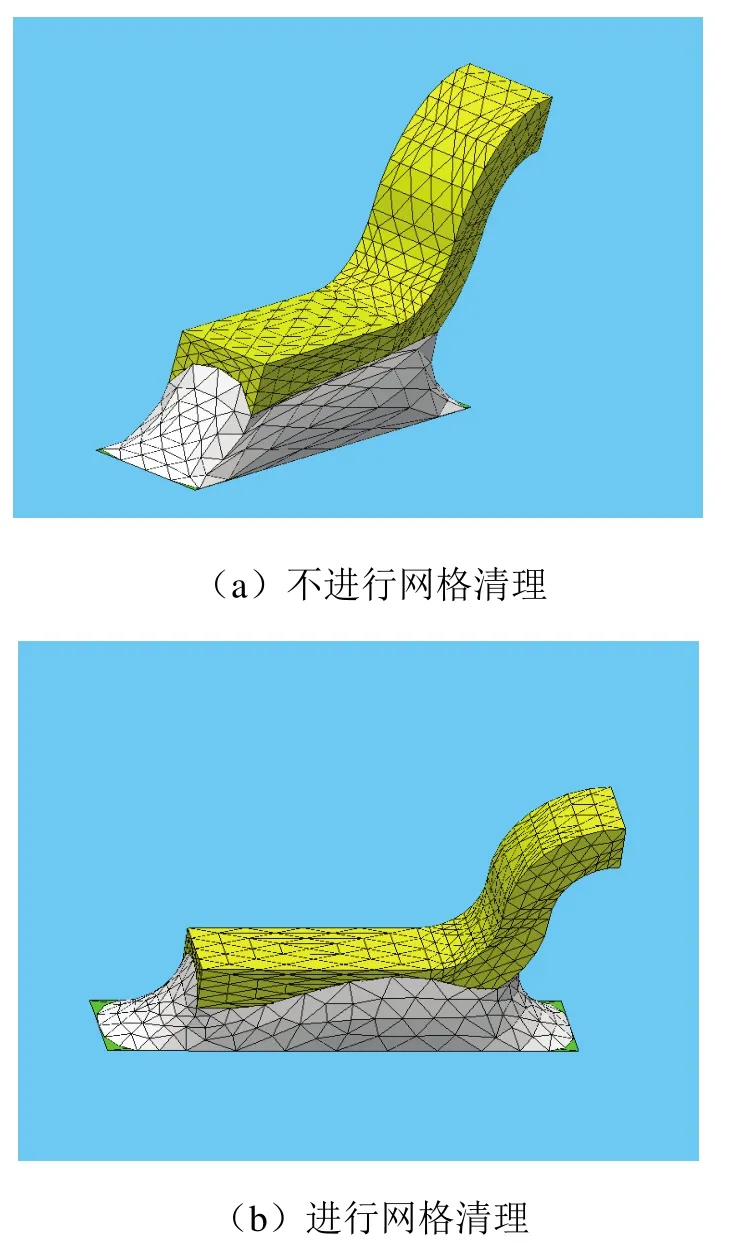
圖3 翼形焊點形態模擬結果

[1] Akay H U, Zhang H, Paydar N H. Experimental Correlation of an Energy-based Fatigue life Prediction Method for Solder Joints[J]．Advances in Electronic Packaging,ASME-EEP, 1997，19（2）：1567-1574．

[2] 王國忠，王春青．SMT焊點形態影響焊點熱循環壽命的試驗研究[J]．電子工藝技術，1997，18（5）：182-184．

[3] Chiang K N，Chen W L. Electronic Packaging Reflow Shape Prediction for The Solder Mask Defined Ball Grid Array[J]．Transactions-American Society of Mechanical Engineers Journal of Electronic Packaging, 1998，120：175-178．

[4] Yang L，Liu W，Wang C，et al．Self-assembly of Three- dimensional Microstructures in MEMS via Fluxless Laser Reflow Soldering[C]//12th International Conference on Electronic Packaging Technology and High Density Packaging (ICEPT-HDP),2011：1-4．

[5] 吳玉秀．QFP焊點可靠性及其翼形引線尺寸的優化模擬[D]．南京：南京航空航天大學，2007：59-65．