基于灰色模型的集裝箱貨量預(yù)測(cè)

鄭 剛

(大連中遠(yuǎn)國(guó)際貨運(yùn)有限公司，遼寧 大連 116001)

基于灰色模型的集裝箱貨量預(yù)測(cè)

鄭 剛

(大連中遠(yuǎn)國(guó)際貨運(yùn)有限公司，遼寧 大連 116001)

為提高集裝箱貨量的預(yù)算精度，根據(jù)灰色模型理論，建立基于GM(1,1)模型的集裝箱貨量預(yù)測(cè)方案，并首次將該模型運(yùn)用到班輪公司集裝箱貨量的預(yù)測(cè)研究中。通過(guò)對(duì)中國(guó)遠(yuǎn)洋和中海集運(yùn)2008—2011年的集裝箱貨量進(jìn)行實(shí)證檢驗(yàn)，證明GM(1,1)模型預(yù)測(cè)效果較好，對(duì)班輪公司宏觀戰(zhàn)略的制定和全面預(yù)算的管理具有重要意義。

交通運(yùn)輸經(jīng)濟(jì)學(xué)；預(yù)測(cè)；灰色模型；GM(1,1);集裝箱量

2013年，世界經(jīng)濟(jì)危機(jī)與希望并存，全球集裝箱班輪業(yè)繼續(xù)掙扎在虧損與盈利的邊緣。集裝箱貨運(yùn)量是班輪公司最重要的經(jīng)營(yíng)數(shù)據(jù)之一，直接關(guān)系到主營(yíng)業(yè)務(wù)的收入和成本，班輪公司發(fā)展戰(zhàn)略的制定和全面預(yù)算的管理離不開(kāi)對(duì)集裝箱貨量的科學(xué)預(yù)測(cè)。但是，在全球政治經(jīng)濟(jì)環(huán)境、市場(chǎng)競(jìng)爭(zhēng)環(huán)境、運(yùn)力投放、航線(xiàn)調(diào)整等諸多不確定因素的影響下，傳統(tǒng)的線(xiàn)性回歸模型已不再適用于集裝箱貨量預(yù)測(cè)，需尋找更加科學(xué)、合理的預(yù)測(cè)模型。

華中科技大學(xué)鄧聚龍[1]教授創(chuàng)建的灰色模型理論適用于樣本空間小、信息資源復(fù)雜的不確定性系統(tǒng)的研究。已有多位學(xué)者[2-11]將該模型應(yīng)用于港口吞吐量的預(yù)測(cè)工作中，并取得了很好的成績(jī)。本文通過(guò)實(shí)證檢驗(yàn)，證明灰色模型在班輪公司集裝箱貨量的預(yù)測(cè)研究中同樣具有較高的精度和實(shí)用價(jià)值。

1 灰色模型理論簡(jiǎn)析

1.1灰色模型的思想

基于灰色模型(Grey Model，GM)的預(yù)測(cè)方法稱(chēng)為灰色預(yù)測(cè)。傳統(tǒng)的預(yù)測(cè)方法要求數(shù)據(jù)樣本量大、數(shù)據(jù)遵循一定的變化趨勢(shì)，而灰色預(yù)測(cè)對(duì)數(shù)據(jù)沒(méi)有特殊要求，應(yīng)用范圍比較廣泛。當(dāng)時(shí)間序列無(wú)明顯變化趨勢(shì)時(shí)，采用累加的方法可生成一個(gè)變化趨勢(shì)明顯的時(shí)間序列，按該數(shù)列的增長(zhǎng)趨勢(shì)可建立預(yù)測(cè)模型，考慮灰色因子的影響進(jìn)行預(yù)測(cè)，然后采用“累減”的方法進(jìn)行逆運(yùn)算，恢復(fù)原時(shí)間序列，得到預(yù)測(cè)結(jié)果。

1.2灰色模型的構(gòu)建

目前使用比較廣泛的灰色預(yù)測(cè)模型是關(guān)于數(shù)列預(yù)測(cè)的一個(gè)變量、一階微分的GM(1, 1)模型。GM(1, 1)的構(gòu)造如下。

設(shè)X(0)=(x(0)(1),x(0)(2),…，x(0)(n))，其中，x(0)(k)≥0,k=1,2，…,n；X(1)為X(0)的一次累加生成序列：X(1)=(x(1)(1),x(1)(2),…,x(1)(n)),其中

(1)

Z(1)為X(1)的緊鄰均值生成序列：Z=(z(1)(2),z(1)(3),…,z(1)(n)), 其中

k=2,3,…,n

(2)

設(shè)待估參數(shù)列為P=[a,b]T，采用最小二乘法確定模型參數(shù)：P=(BTB)-1BTY

(3)

(4)

將式(4)代入式(3)，并解微分方程，可得白化方程的解為

k=1,2,…,n

(5)

預(yù)測(cè)模型計(jì)算所得的結(jié)果為一次累加生成值的預(yù)測(cè)值，需對(duì)其進(jìn)行一次累減還原才能得到原始值的預(yù)測(cè)值。

(6)

1.3灰色模型的檢驗(yàn)

灰色理論建模可采用3種檢驗(yàn)方式，即殘差檢驗(yàn)、關(guān)聯(lián)度檢驗(yàn)和后驗(yàn)差檢驗(yàn)。殘差檢驗(yàn)是按點(diǎn)檢驗(yàn)的，屬于算術(shù)檢驗(yàn)；關(guān)聯(lián)度檢驗(yàn)是根據(jù)模型曲線(xiàn)與行為數(shù)據(jù)曲線(xiàn)的幾何相似程度進(jìn)行檢驗(yàn)的，屬于幾何檢驗(yàn)；后驗(yàn)差檢驗(yàn)是按照殘差的概率分布進(jìn)行檢驗(yàn)的，屬于統(tǒng)計(jì)檢驗(yàn)。

1.3.1殘差

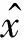
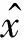
(7)

(8)

1.3.2關(guān)聯(lián)度

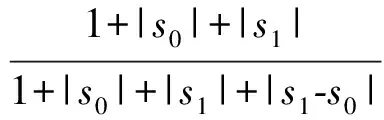
(9)

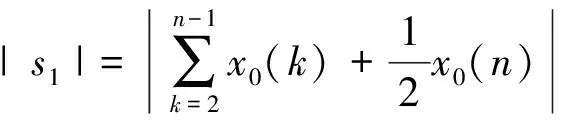
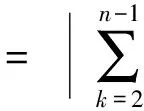
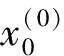
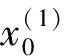
1.3.3后驗(yàn)差

(10)

(11)

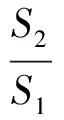
如果模型能夠通過(guò)殘差檢驗(yàn)、關(guān)聯(lián)度檢驗(yàn)和后驗(yàn)差檢驗(yàn)，則可用所建模型進(jìn)行預(yù)測(cè)；否則，需要對(duì)模型進(jìn)行殘差修正。模型精度檢驗(yàn)等級(jí)見(jiàn)表1。

表1 模型精度檢驗(yàn)等級(jí)

2 基于GM(1,1)的集裝箱貨量預(yù)測(cè)

2.1樣本數(shù)據(jù)

根據(jù)中國(guó)遠(yuǎn)洋(SH.601919)近年公布的集裝箱貨運(yùn)量數(shù)字，利用GM(1,1)模型對(duì)2012年該公司集裝箱貨運(yùn)量進(jìn)行預(yù)算，樣本數(shù)據(jù)序列見(jiàn)表2。

表2 2008—2011年中國(guó)遠(yuǎn)洋集裝箱貨運(yùn)量 TEU

2.2模型建立

按照表2的數(shù)據(jù)，構(gòu)造原始時(shí)間序列：

X(0)=(5 792 593,5 234 292,6 215 371,6 910 041)

一次累積生成序列：

X(1)=(5 792 593,11 026 885,17 242 256,

24 152 297)

緊鄰均值生成序列：

Z(1)=(8 409 739,14 134 570.5,20 697 276.5)

可知

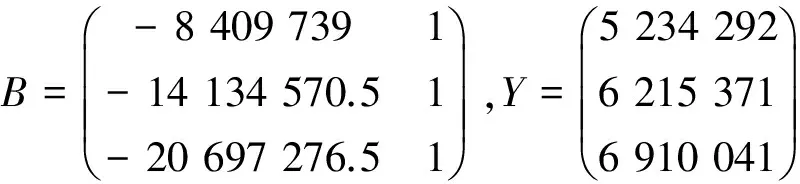
利用最小二乘法求得參數(shù)列

建立中國(guó)遠(yuǎn)洋集裝箱貨運(yùn)量預(yù)測(cè)模型為

(5 792 593+30 705 541)e0.135 638k-30 705 541

2.3模型預(yù)測(cè)及精度檢驗(yàn)

依據(jù)創(chuàng)建模型預(yù)測(cè)集裝箱貨運(yùn)箱量，并計(jì)算絕對(duì)誤差和相對(duì)誤差(見(jiàn)表3)。

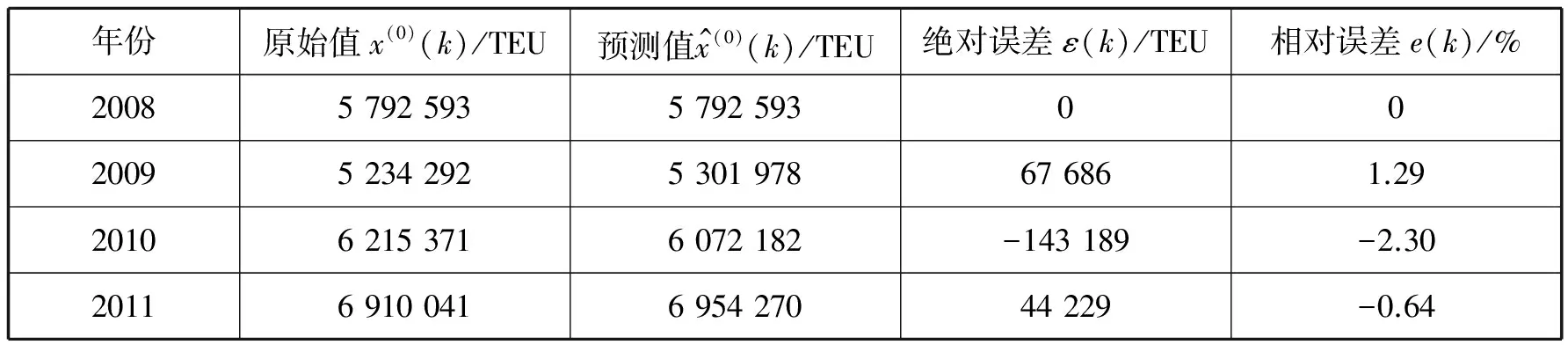
表3 2008—2011年中國(guó)遠(yuǎn)洋集裝箱貨運(yùn)量預(yù)測(cè)值及誤差

1) 殘差檢驗(yàn)：平均相對(duì)誤差為1.412 336%，預(yù)測(cè)誤差比較小。

2) 關(guān)聯(lián)度檢驗(yàn)：絕對(duì)關(guān)聯(lián)度為0.936 9gt;0.90，原始序列于預(yù)測(cè)序列關(guān)聯(lián)度很高。

3) 后驗(yàn)差檢驗(yàn)：方差比C=0.137lt;0.35，小概率誤差P=1gt;0.95。

因此，判定模型等級(jí)為I級(jí)，不需要對(duì)模型進(jìn)行修正，模型預(yù)測(cè)精度高。

利用上述GM(1,1)模型，對(duì)2012—2015年中國(guó)遠(yuǎn)洋集裝箱貨運(yùn)量進(jìn)行預(yù)測(cè)(見(jiàn)表4)。

表4 2012—2015年中國(guó)遠(yuǎn)洋集裝箱貨運(yùn)量預(yù)測(cè) TEU

預(yù)測(cè)2012年中國(guó)遠(yuǎn)洋集裝箱貨運(yùn)箱量可達(dá)796.4萬(wàn)TEU，2013年將達(dá)到912萬(wàn)TEU。

2.4對(duì)中海集運(yùn)(SH.601866)的集裝箱貨量預(yù)測(cè)

參照上述方法，對(duì)國(guó)內(nèi)第二大集裝箱班輪公司中海集運(yùn)(SH.601866)建立GM(1,1)模型為

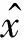
(6 942 148+129 441 927)e0.048 59k-129 441 927

該模型等級(jí)也為I級(jí)，預(yù)測(cè)結(jié)果見(jiàn)表5。

表5 2012—2015年中海集運(yùn)集裝箱貨運(yùn)量預(yù)測(cè) TEU

預(yù)測(cè)2012年中海集運(yùn)的集裝箱貨運(yùn)量可達(dá)784.8萬(wàn)TEU，2013年將達(dá)到823.9萬(wàn)TEU。

2.5實(shí)證檢驗(yàn)

根據(jù)中國(guó)遠(yuǎn)洋和中海集運(yùn)公布的2012年年報(bào)，實(shí)際貨運(yùn)量和預(yù)測(cè)的誤差見(jiàn)表6。

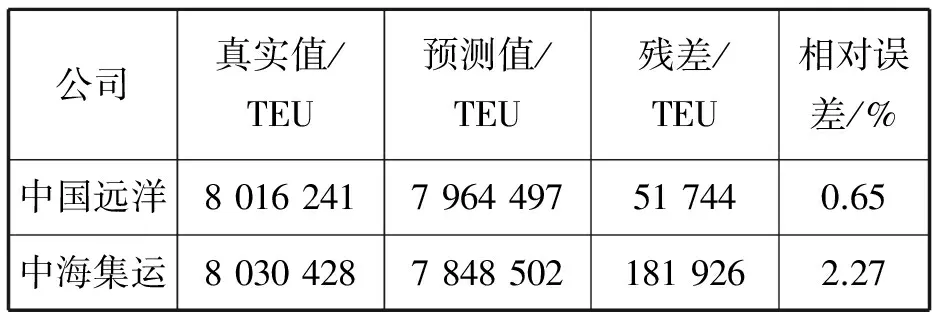
表6 2012年預(yù)測(cè)箱量和實(shí)際箱量

2012年初，中國(guó)遠(yuǎn)洋自身預(yù)測(cè)當(dāng)年貨量730萬(wàn)TEU，而實(shí)際完成801.6萬(wàn)TEU。顯然，灰色模型預(yù)測(cè)結(jié)果誤差很小，精度很高，具有較高的實(shí)用價(jià)值。

4 結(jié) 語(yǔ)

GM(1,1)模型具有無(wú)限增長(zhǎng)的特性，即當(dāng)時(shí)間無(wú)窮大時(shí)所得的預(yù)測(cè)結(jié)果也將趨向于無(wú)窮大。因此，灰色模型在集裝箱貨量的短期預(yù)測(cè)中是適用的，而中長(zhǎng)期預(yù)測(cè)的結(jié)果的可靠性就明顯偏弱，所以一般只選取前兩個(gè)預(yù)測(cè)數(shù)據(jù)值。

即便如此，通過(guò)上述實(shí)證研究，證明灰色模型可以成功地預(yù)測(cè)集裝箱貨量，對(duì)班輪公司戰(zhàn)略制定和全面預(yù)算工作具有重要意義，值得借鑒、推廣。

[1] 鄧聚龍.灰理論控制[M].武漢:華中理工大學(xué)出版社,2002.

[2] 曾波,孟偉.面向特殊序列的灰色預(yù)測(cè)建模方法[M].重慶:重慶大學(xué)出版社,2011.

[3] 黨耀國(guó),劉思峰,王正新，等.灰色預(yù)測(cè)與決策模型研究[M].北京:科學(xué)出版社,2009.

[4] 歐陽(yáng)凱,袁松寶,劉俐.基于灰色模型的我國(guó)物流產(chǎn)業(yè)增加值預(yù)測(cè)[J].物流工程與管理, 2011，33(11):61-63.

[5] 陳淑燕,陳家勝.一種改進(jìn)的灰色模型在交通量預(yù)測(cè)中的應(yīng)用[J].公路交通科技,2004，21(2)：80-83.

[6] 周茵.殘差灰色預(yù)測(cè)模型在物流需求預(yù)測(cè)中的應(yīng)用[J].鐵道運(yùn)輸與經(jīng)濟(jì),2007(11):59-61.

[7] 楊中慶，趙彬彬，廖慧敏.灰色組合模型在港口集裝箱吞吐量預(yù)測(cè)中的應(yīng)用[J].水運(yùn)工程, 2006(9):14-15.

[8] 施澤軍,李凱.基于灰色模型和指數(shù)平滑法的集裝箱吞吐量預(yù)測(cè)[J]. 重慶交通大學(xué)學(xué)報(bào):自然科學(xué)版, 2008,27(2):302-304.

[9] 鐘霞，吳中，王麗.灰色理論及其組合模型在交通運(yùn)量預(yù)測(cè)中的運(yùn)用[J].交通標(biāo)準(zhǔn)化,2004(12):36-39.

[10] 萬(wàn)軼凌，朱士東.組合預(yù)測(cè)在水路貨運(yùn)量預(yù)測(cè)中的應(yīng)用[J].交通與運(yùn)輸,2006(2):27-29.

[11] 虞亞平，王冠中，李大治.廣義灰色關(guān)聯(lián)度的簡(jiǎn)便計(jì)算方法[J].南通大學(xué)學(xué)報(bào)：自然科學(xué)版,2008，7(2):85-90.

GreyModelforPredictionofContainerShipment

ZHENGGang
(Dalian International Freight Co., Ltd, Dalian 116001, China)

The study was designed to predict the quantity of container shipment. The method used in this study is gray system model GM(1,1). With shipping data between 2008 and 2012, the prediction technology is used to forecast the container shipment of COSCON and CSCL. Test results indicate that GM(1,1) model is of higher adaptability and accuracy.The research is of great value to the managment of shiping company.

prediction; gray mode; GM(1,1); container shipment

2014-01-10

鄭 剛(1974-),男,山東肥城人，工程師，碩士生，從事集裝箱管理及市場(chǎng)預(yù)測(cè)研究。E-mail: zhg@sanly.cn.

1000-4653(2014)02-0118-04

F552

A