重視邏輯思維 提高解題能力

◆王洪富

(山東省昌邑市石埠鎮(zhèn)石埠初級(jí)中學(xué))

在數(shù)學(xué)教學(xué)中，我們常常會(huì)發(fā)現(xiàn)許多學(xué)生對(duì)圖形處理技能和推理論證技能比較薄弱。幾何對(duì)于中學(xué)生來(lái)說(shuō)是個(gè)重點(diǎn)也是難點(diǎn)。數(shù)學(xué)教學(xué)與思維的關(guān)系十分密切。隨著現(xiàn)代教育技術(shù)的發(fā)展和教育理念的不斷更新，初中數(shù)學(xué)教學(xué)的任務(wù)已不僅僅是使學(xué)生獲取基礎(chǔ)知識(shí)，而是更側(cè)重于學(xué)生思維能力的發(fā)展，培養(yǎng)學(xué)生自覺(jué)地運(yùn)用數(shù)學(xué)知識(shí)去分析、解決日常生活中問(wèn)題的能力，從而形成良好的思維品質(zhì)。下面談一談我自己在教學(xué)實(shí)踐中的幾點(diǎn)體會(huì)。

一、合作探究，營(yíng)造創(chuàng)造性思維的環(huán)境

提及合作，教師腦海中大多會(huì)出現(xiàn)這樣一種教學(xué)流程:教師出示思考題——學(xué)生討論——匯報(bào)討論結(jié)果。初一看，流程清楚，學(xué)生討論積極、氣氛活躍，參與面廣，似乎學(xué)生的主體作用得以真正發(fā)揮。然而，不妨冷靜地思考，作為具有思維獨(dú)特性的個(gè)體——學(xué)生，他獨(dú)立思考的時(shí)間得到保證了嗎?當(dāng)問(wèn)題呈現(xiàn)后，教師不引導(dǎo)學(xué)生認(rèn)真分析、認(rèn)真思考就組織學(xué)生討論，必然導(dǎo)致討論流于形式、淺嘗輒止。特別是那些“慢知”的學(xué)生，要么默默無(wú)聞，要么人云亦云。教師在組織學(xué)生合作交流前要留給學(xué)生思考的時(shí)間，先讓每個(gè)學(xué)生獨(dú)立精心分析、凝神思索，然后再進(jìn)行小組交流，思維碰撞，集聚團(tuán)體智慧，形成優(yōu)化方案，這樣每個(gè)學(xué)生都有思考的時(shí)間，都有表達(dá)自己觀點(diǎn)的機(jī)會(huì)，才能形成真正意義上的思維碰撞與智慧共享。只有在這種氛圍中，學(xué)生才能充分發(fā)揮自己的聰明才智。課堂教學(xué)中有意識(shí)地搞好合作教學(xué)，設(shè)計(jì)集體討論、查缺互補(bǔ)、分組操作等內(nèi)容，鍛煉學(xué)生的合作能力。特別是一些不易解決的問(wèn)題，讓學(xué)生在班集體中開(kāi)展討論，這是營(yíng)造創(chuàng)新環(huán)境發(fā)揚(yáng)教學(xué)民主環(huán)境的表現(xiàn)在班集體中。學(xué)生在輕松環(huán)境下，暢所欲言，各抒己見(jiàn)，學(xué)生敢于發(fā)表獨(dú)立的見(jiàn)解，或修正他人的想法，或?qū)讉€(gè)想法組合為一個(gè)更佳的想法，從而在學(xué)習(xí)過(guò)程中，培養(yǎng)學(xué)生思維的嚴(yán)密性。

二、加強(qiáng)數(shù)學(xué)語(yǔ)言教育，訓(xùn)練學(xué)生用精練簡(jiǎn)明的書(shū)面語(yǔ)言表達(dá)的能力

數(shù)學(xué)語(yǔ)言是信息的數(shù)學(xué)化表示形式，它是數(shù)學(xué)思維的載體，也是數(shù)學(xué)信息處理和交流的工具。使用數(shù)學(xué)語(yǔ)言，狹義地說(shuō)可以提高數(shù)學(xué)思維效率;廣義地說(shuō)，它適應(yīng)了“數(shù)學(xué)社會(huì)化和社會(huì)數(shù)學(xué)化”的信息處理需要。教給學(xué)生嫻熟的數(shù)學(xué)語(yǔ)言，是培養(yǎng)學(xué)生數(shù)學(xué)素養(yǎng)的一個(gè)重要方面。數(shù)學(xué)語(yǔ)言包括自然語(yǔ)言、圖像語(yǔ)言和符號(hào)語(yǔ)言。教學(xué)中，要充分運(yùn)用并創(chuàng)設(shè)這種語(yǔ)言使用良好環(huán)境，讓學(xué)生投身于數(shù)學(xué)語(yǔ)言環(huán)境學(xué)習(xí)數(shù)學(xué)語(yǔ)言，使用數(shù)學(xué)語(yǔ)言，用數(shù)學(xué)語(yǔ)言表達(dá)思想、解決問(wèn)題。一定要逐步使學(xué)生適應(yīng)這種嚴(yán)格的推理方式，并且在書(shū)寫(xiě)上能反映出來(lái)。特別是在幾何的教學(xué)上，一定要重視這種邏輯的演繹，這也是訓(xùn)練邏輯推理能力的有效方法。

狠抓幾何語(yǔ)言訓(xùn)練:(1)要求學(xué)生理解和熟記幾何常用語(yǔ)。加強(qiáng)學(xué)生的理解，為了讓學(xué)生熟記“幾何常用語(yǔ)”，經(jīng)常組織學(xué)生在課堂上練習(xí)和學(xué)說(shuō)，以提高他們的口頭表達(dá)能力。

(2)將定義、定理等翻譯成符號(hào)語(yǔ)言，并畫(huà)出圖形，符號(hào)語(yǔ)言能將文字語(yǔ)言與圖形結(jié)合起來(lái)，有利于學(xué)生理解幾何概念的本質(zhì)屬性，也為文字證明打下基礎(chǔ)

(3)編寫(xiě)范句，形成規(guī)范的書(shū)寫(xiě):如延長(zhǎng)_____到點(diǎn)____，使_____=____。此外，我講課時(shí)，努力做到語(yǔ)言規(guī)范化。對(duì)幾何語(yǔ)言的教學(xué)，我是隨著幾何知識(shí)的教學(xué)逐步進(jìn)行，通過(guò)培養(yǎng)和訓(xùn)練學(xué)生的幾何語(yǔ)言，使學(xué)生的思維能力在探討中進(jìn)一步得以發(fā)展。

三、變式教學(xué)，感悟共性，培養(yǎng)求同存異的思維能力

變式其實(shí)就是創(chuàng)新。當(dāng)然變式不是盲目的變，應(yīng)抓住問(wèn)題的本質(zhì)特征，遵循學(xué)生認(rèn)知心理發(fā)展，根據(jù)實(shí)際需要進(jìn)行變式。實(shí)施變式訓(xùn)練應(yīng)抓住思維訓(xùn)練這條主線，恰當(dāng)?shù)淖兏鼏?wèn)題情境或改變思維角度，培養(yǎng)學(xué)生的應(yīng)變能力，引導(dǎo)學(xué)生從不同途徑尋求解決問(wèn)題的方法。通過(guò)多問(wèn)、多思、多用等激發(fā)學(xué)生思維的積極性和深刻性。另外，由于巧妙設(shè)計(jì)變式于課堂教學(xué)中，學(xué)生感到課堂的豐富多彩，從而增強(qiáng)課堂的趣味性。

如“直角三角形斜邊上的中線是斜邊的一半”學(xué)生在剛學(xué)完這一性質(zhì)時(shí)還不會(huì)靈活運(yùn)用，對(duì)于這一性質(zhì)相當(dāng)陌生，這時(shí)教師就可通過(guò)一系列變式訓(xùn)練來(lái)加深學(xué)生的理解，

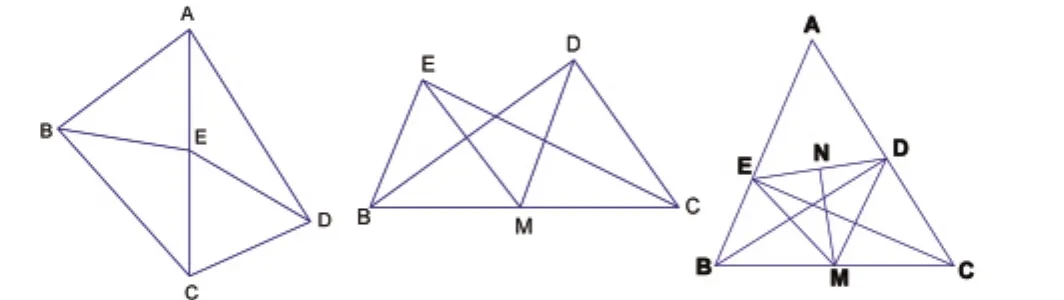
題1:如圖，已知△ABC和△ADC為直角三角形，點(diǎn)E為AC中點(diǎn)，求證:BE=DE.

題2:如圖，已知△BCE和△BCD為直角三角形，點(diǎn)M為BC中點(diǎn)，求證:EM=DM.

題3:如圖:已知BD、CE分別是△ABC的高，M、N分別是BC、DE的中點(diǎn)，分別連結(jié) ME、MD.求證:MN⊥ED.

通過(guò)以上三題的變式訓(xùn)練，學(xué)生應(yīng)該可以很容易感悟出它們之間的共性，都是通過(guò)直角三角形的這一性質(zhì)來(lái)證明線段相等，相信以后在遇到類(lèi)似問(wèn)題時(shí)學(xué)生的反應(yīng)就會(huì)快很多，在此基礎(chǔ)上再來(lái)解決書(shū)上的這一例題就會(huì)方便很多。

四、引導(dǎo)學(xué)生自主探索，培養(yǎng)思維品質(zhì)

鼓勵(lì)學(xué)生獨(dú)立思考，課堂教學(xué)的時(shí)間是有限的，教師必須把握好學(xué)生自主探索活動(dòng)的時(shí)間，給最終的歸納總結(jié)留有余地。給學(xué)生自主探索適當(dāng)?shù)目臻g，探索過(guò)程中獲得的結(jié)果固然重要，探索過(guò)程本身也具有重要價(jià)值。對(duì)于學(xué)生的探索活動(dòng)，教師不僅要給予啟發(fā)、引導(dǎo)，而且應(yīng)適時(shí)地進(jìn)行歸納，明晰進(jìn)一步探索的思路。對(duì)于進(jìn)行自主探索有困難的學(xué)生，教師應(yīng)給以具體的幫助、鼓勵(lì)和指導(dǎo)，努力使他們也能參與探索活動(dòng)。

數(shù)學(xué)教學(xué)是數(shù)學(xué)思維活動(dòng)的教學(xué)，因此，數(shù)學(xué)素質(zhì)的培養(yǎng)主要表現(xiàn)在教學(xué)活動(dòng)中對(duì)學(xué)生思維品質(zhì)的培養(yǎng)。科學(xué)的思維方法主要有十種，它們分別是:分析與綜合，抽象和概括，系統(tǒng)化和具體化，比較和歸類(lèi)，歸納和演繹。在引導(dǎo)學(xué)生自主探索教學(xué)過(guò)程中我們要緊密結(jié)合教材內(nèi)容，掌握學(xué)生思維活動(dòng)的心理規(guī)律，有計(jì)劃、有目的地教給學(xué)生科學(xué)的思維方法，以綜合他們的學(xué)習(xí)能力和創(chuàng)造精神。優(yōu)質(zhì)的思維品質(zhì)是指思維具備深刻性、敏銳性、批判性和創(chuàng)造性。挖掘教材，培養(yǎng)思維的深刻性，應(yīng)通過(guò)知識(shí)形成過(guò)程引導(dǎo)學(xué)生進(jìn)行數(shù)學(xué)抽象和概括，明確知識(shí)間的聯(lián)系，把握知識(shí)的結(jié)構(gòu)，培養(yǎng)思維的敏銳性。

五、成功是最好的激勵(lì)

掌握數(shù)學(xué)知識(shí)后的愉快情緒體驗(yàn)，能使學(xué)生得到心理上的補(bǔ)償和滿足，激勵(lì)他們獲得更多的成功。通過(guò)這種方式，使得抽象的數(shù)學(xué)概念成為看得見(jiàn)、摸得著的東西，從而內(nèi)化到學(xué)生的知識(shí)結(jié)構(gòu)中，從而取得較好的教學(xué)實(shí)效。

實(shí)踐證明，思維能力的培養(yǎng)并不是完全不可捉摸的，培養(yǎng)學(xué)生邏輯思維能力，要有一個(gè)較長(zhǎng)的過(guò)程，不能操之過(guò)急，必須有意識(shí)、有計(jì)劃地從簡(jiǎn)單到復(fù)雜循序漸進(jìn)，使學(xué)生逐步學(xué)會(huì)推理論證的方法。增強(qiáng)對(duì)概念的理解深度。