基于相平面法的變PID控制算法

楊 樂，樊澤明，王惠萌，閆鴻雁

（1.西北工業大學自動化學院，陜西 西安 710129；2.西北工業大學航海學院，陜西 西安 710129）

0 引言

PID 控 制 器 （proportional integral derivative controller，亦稱PID調節器）是目前控制領域應用最廣泛的一種常規控制器，具有原理簡單、易于實現、魯棒性強等優點。在工業過程控制中，PID類型的控制技術占有主導地位［1－2］。

PID控制器由比例單元P、積分單元I和微分單元D組成，通過Kp，Ki和Kd三個參數設定。PID控制器主要適用于基本線性和動態特性不隨時間變化的系統［3］。但傳統的數字PID控制算法針對某些非線性和動態特性差的系統，控制效果并不理想。本文針對此問題，提出了基于相平面法的變PID控制算法。

1 PID控制算法簡介

在計算機控制算法中，經常用到理想微分的PID控制算法［4］。該控制算法是對連續生產過程中的PID控制算法進行離散化而得到的。在連續域中PID控制器的表達式［5］見公式（1）。

式（1）中：u為控制量；Kp，Ki和Kd為分別為比例、積分和微分參數；e為偏差。

對該式進行離散化，可分別得到位置型和增量型的理想微分的PID控制算法［5］。位置型算法見公式（2），增量型算法見公式（3）。

由于該離散差分方程是由一階差分近似法得到的，所以變換精度較差，變換后系統的單位脈沖響應和頻率特性都有較大的差別，因此仍有很多待改進的地方。特別是在系統的動態特性較差的時候，傳統PID控制算法的運算結果并不理想；另一方面，積分項的不穩定性，也使得控制器在穩態誤差減小的同時，動態性能和穩定性變差；同時，傳統的PID算法自始至終都使用相同的控制算法來進行控制，缺少相應的對應性，也使得系統的整體性能并不理想。

通過利用相平面分析法對傳統的PID算法進行了改進，得到了基于相平面法的PID變策略算法，這種算法利用相平面圖像對系統的響應過程進行實時分析，在系統的不同狀態下使用不同的控制策略，達到“對癥下藥”效果，消除了傳統PID算法積分項帶來的不穩定性，避免了傳統PID算法缺少對應性的問題，使整個系統性能大幅提升。

2 基于相平面法的變PID控制算法

2.1 控制誤差的相平面法分析

相平面法（phase plane method）是 Poincare H于1885年首先提出來的，它是求解一、二階線性或非線性系統的一種圖解法，通過圖解法將一階和二階系統的運動過程轉化為位置和速度平面上的相軌跡，比較直觀、準確地反映系統的穩定性、平衡狀態和穩態精度［6］。該方法主要用來分析系統的穩定性［7］。

以系統的誤差為橫坐標，誤差的導數為縱坐標（在相平面中分別用e和e′表示），可以利用相平面圖描繪出系統的響應過程，根據響應過程的不同階段，可以將相平面劃分成若干區域［8］，如圖1所示。

如果用M表示誤差上下界，ε和ε′分別表示e和e′要求的精度，根據一般系統的響應，可對系統在不同時刻所處于的相平面的不同區域作以下分析［9］：

1）當系統處于C1或C2區域時，即｜e（k）｜＞M時，表明系統誤差很大，此時應該使系統誤差盡可能快地減小。

2）當系統處于C3區域時，即e（k）＜ε且e′（k）＜ε′時，表明系統已經達到控制要求，此時應該保持該狀態，使系統誤差保持在規定范圍內。

3）當系統處于C4到C9區域時，表明系統正在趨于一個由誤差較大到規定誤差范圍內的過程中（系統穩定的情況下），在該過程中根據e（k）／e′（k）的大小，對系統響應的不同時刻的誤差特征進行分類，確定該時刻系統所在的相平面，根據所在的相平面采用不同的控制策略。

圖1 相平面區域的劃分Fig.1 The division of phase plane area

2.2 基于相平面法的變PID控制算法簡介

一般的被控對象都具有自平衡能力，在控制過程中不同時間段會有不同的特征，通過對這些特征的分析，可以改變PID控制算法的控制策略［10］。即，可以通過其響應的不同階段，反映在相平面的不同區域，采用P（比例）控制，PI（比例、積分）控制，PD（比例、微分）控制和PID（比例、積分、微分）控制等不同策略，對當前情況進行控制，以達到比例、積分、微分三個控制項的最優化利用。其算法的控制過程［11］，如圖2所示。

圖2 PID控制過程框圖Fig.2 PID control process block diagram

2.3 基于相平面法的變PID控制算法設計

由于系統在不同的響應階段需要有不同的控制算法，通過對每個控制周期的誤差進行分析，得到相應的控制效果最好的控制策略，并確定該時刻的控制算法：

1）若誤差值的絕對值大于設定誤差閾值M，即｜e（k）｜＞M時，說明系統處于C1或C2區，這時控制器應該采用最大（或最小）輸出，使系統以最快速度減小當前誤差。

2）若誤差值和誤差導數值同時小于目標誤差，即e（k）＜ε且e′（k）＜ε′時，說明系統處于C1區，表明系統誤差已經達到控制系統的精度要求，這時控制器使用PI控制，引入積分控制以控制穩態誤差。

3）在穩定過程中，若系統處于C4區，說明此時誤差相對較大，仍使用全功率輸出可能會造成超調過大；同時，C4區沒有引入積分項和微分項，是由于在誤差大的情況下引入積分項可能導致積分飽和，影響系統的動態性能；過早地引入微分也會使系統產生不穩定，因此只采用比例控制，即P控制。

4）C5和C8兩個區域同處于一個誤差和誤差導數不是很大的范圍，因此采用PID控制，這樣可以有效避免由于積分分離而導致系統產生過大的殘差。

5）C6和C7兩個區域同處于一個誤差的導數較大而誤差較小的范圍，在此范圍加入微分項可以有效抑制系統的超調，使得系統的超調有所減小。

6）C9區域是一個有較大反向誤差的區域，在此引入PI控制可以達到消除積分飽和的目的，減小積分項的累積量，使得系統的快速性有所改善。

綜上所述，各個相平面區域的控制模式見表1。表1中，U表示當前控制量的輸出；e（k）表示該時刻系統誤差，e（k－1）表示上一個控制周期的系統誤差，e（k－2）類推。

表1 各個相平面區域的控制模式Tab.1 The control mode of each phase plane area

3 Matlab仿真設計

3.1 控制對象

系統的離散方程組見公式（4）。

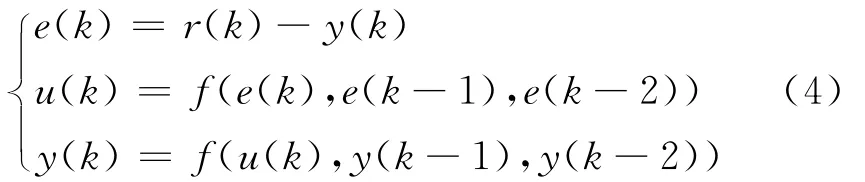
式（4）中：e（k）—k時刻的偏差；r（k）—k時刻的輸入量；y（k）—k時刻的輸出量；u（k）—k時刻的控制量。

對同一系統使用不同的控制方案進行控制分析，選取相同的Kp，Ki和Kd參數進行仿真控制，并對結果進行對比分析。

3.2 實驗結果及分析

3.2.1 比例項實驗

選取Kp＝10，Ki＝0，Kd＝0，得到的仿真結果如圖3所示。

圖3 Kp＝10，Ki＝0，Kd＝0時的仿真結果Fig.3 The simulation result when Kp ＝10，Ki ＝0，Kd ＝0

由圖3可以看到，如果僅使用P控制，相平面PID和普通PID動態性能相當，但穩態誤差有所減少，說明當僅有P控制時，該控制器性能相對優越。

3.2.2 積分項實驗

圖4 Kp＝10，Ki＝0.15，Kd＝0時的仿真結果Fig.4 The simulation result when Kp ＝10，Ki＝0.15，Kd＝0

選取Kp＝10，Ki＝0.15，Kd＝0，得到的仿真結果如圖4所示。由圖4可見，該控制狀態下的穩態誤差較大，為了消除穩態誤差，又引入了積分項進行控制。當控制器引入積分項時，普通PID控制系統發生明顯的震蕩，動態性能變差，但相平面的PID控制器控制動態性能好，超調小，調節時間短。

進一步增加積分項，選取Kp＝10，Ki＝0.3，Kd＝0，得到的仿真結果如圖5所示。

圖5 Kp＝10，Ki＝0.3，Kd＝0時的仿真結果Fig.5 The simulation result when Kp＝10，Ki＝0.3，Kd＝0

由圖5可見，普通PID控制器已經發散，不能達到控制效果，而相平面的PID控制器控制效果仍然良好。當普通PID控制器有較大改變時，偏差較大，在積分項的作用下，往往會產生過大超調和長時間波動，甚至引起系統的不穩定；而相平面PID控制器采用了積分分離，這樣就使得僅當誤差相對較小時才引入積分項，對普通PID的積分項進行了改進。

3.2.3 微分項實驗

選取Kp＝10，Ki＝0.15，Kd＝3，得到的仿真結果如圖6所示。

圖6 Kp＝10，Ki＝0.15，Kd＝3時的仿真結果Fig.6 The simulation result when Kp ＝10，Ki＝0.15，Kd ＝3

由圖6可見，該控制狀態下的動態性能還不是很理想，為了改善系統的動態性能，再加入微分項。選取Kp＝10，Ki＝0.2，Kd＝8，得到的仿真結果如圖7所示。

圖7 Kp＝10，Ki＝0.2，Kd＝8時的仿真結果Fig.7 The simulation result when Kp ＝10，Ki＝0.2，Kd＝8

由圖7可見，加入微分項，使得控制系統的動態特性有所增強，當持續增大微分項時，雖然相平面的PID控制超調會比普通PID控制大，但此過程中，普通PID控制器的控制曲線向右移動，動態性能變差，而相平面PID非但不會，反而震蕩幅值變小。

4 結論

通過對系統響應的不同時段進行相應的誤差分析，得到了一種基于相平面的變PID控制算法，該算法通過系統所處的不同時刻，采用不同的控制策略，其性能明顯優于傳統PID控制。并對兩種算法進行了仿真對比，得到以下結論：

1）改進的控制器相對于普通PID控制器有更好的穩定性，對積分項的處理優于傳統PID，積分項的分離也使得控制器在消除靜態誤差時的能力更強，并且不存在殘差，其控制效果明顯優于普通PID控制。

2）該算法可以根據控制人員的不同需要，靈活地改變M，ε和相平面區域線的斜率等的大小，從而達到不同的控制精度，同時使得控制方法和控制手段更加靈活，針對某些非線性和動態特性差的系統有更好的適應性，可滿足不同工程的控制需求。

3）根據控制的不同需要，控制人員可以自行設定相平面中不同區域的控制策略，這就使得該控制算法的改進方式更多，且改進簡單易行，以便適應不同工程領域的不同控制特點。

［1］胡包鋼，應浩.模糊PID控制技術研究發展回顧及其面臨的若干重要問題［J］.自動化學報，2001，27（4）：557－584.

［2］Chen G .Conventional and Fuzzy PID Controllers［J］.An Overview Int.J of Intelligent Control ＆ Systenms，1996（1）：235－246.

［3］黃友銳，曲立國.PID控制器參數整定與實現［M］.北京：中國科學出版社，2010.

［4］王錦標.計算機控制系統［M］.2版.北京：清華大學出版社，2008.

［5］馮衛星，樊澤明，王亮.智能閥門定位器PID參數自整定及控制算法設計［J］.機床與液壓，2009，37（11）：143－144，147.

［6］張吉禮，歐進萍，于達仁.基于相平面軌跡特征的規則自調整模糊控制方法［J］.控制理論與應用，2004，20（04）：607－611.

［7］劉叔軍，蓋曉華.相平面分區控制閉環特性的分析與仿真［J］.南陽理工學院學報，2009，1（01）：12－16.

［8］王鳴.一種換熱器的變PID參數的整定方法及其實現［J］.自動化儀表，2001，22（05）：18－19.

［9］王子謙，薛履中.簡化的模糊PID控制器研究［J］.自動化儀表，2006，27（04）：4－7.

［10］陶永華.新型PID控制及其應用［M］.北京：機械工業出版社，1998.

［11］盧京潮.自動控制原理［M］.西安：西北工業大學出版社，2009.