成敗型系統(tǒng)可靠性增長的Bayes評估

袁 昆 李曉鋼

(北京航空航天大學(xué) 可靠性與系統(tǒng)工程學(xué)院，北京100191)

產(chǎn)品研制，特別是大型復(fù)雜產(chǎn)品的研制過程中，在產(chǎn)品可靠性和性能指標沒有達到預(yù)定目標之前，通常會反復(fù)經(jīng)歷試驗—分析—改進—再試驗的過程，以改進暴露出來的缺陷和增強可靠性.由于改進措施的引進，使得產(chǎn)品可靠性從總體上不再服從同一分布，而是呈現(xiàn)動態(tài)增加的趨勢.在產(chǎn)品設(shè)計定型前要求可靠度必須達到門限值，而實際情況不允許有大樣本提供，因此Bayes理論結(jié)合現(xiàn)場試驗數(shù)據(jù)的方法多被用來實現(xiàn)最終階段的可靠性評估.

在產(chǎn)品確定定型前，往往會進行可靠性增長試驗，以驗證產(chǎn)品可靠性是否滿足要求.而如何利用可靠性增長試驗評估可靠性，目前提出的主要的可靠性增長模型主要包括 Smith模型［1］、Barlow-Scheuer模型［2］、Logistic 模型［3］、折合因子法［4］等.這些模型往往基于無信息先驗分布或者對各階段增長試驗信息進行折合，能給出當(dāng)前試驗階段結(jié)束時的可靠性估計，但無法給出產(chǎn)品的最終可靠性.McLaren［5］將當(dāng)前階段的試驗數(shù)據(jù)與之前階段的試驗數(shù)據(jù)、糾正措施結(jié)合起來，提出了一種迭代過程，并采用均方誤差來評價模型的優(yōu)劣.Nicholls等人［6］在假設(shè)成敗型產(chǎn)品總失效個數(shù)服從泊松分布的基礎(chǔ)上，認為各階段失效發(fā)生概率服從Dirichlet分布，推導(dǎo)出可靠度的Bayes估計.為克服以往Bayes分析模型的缺點，Mazzuchi和Soyer［7］提出了基于次序 Dirichlet先驗分布的可靠性增長模型，利用次序Dirichlet分布的邊緣分布和聯(lián)合分布能夠很好地結(jié)合專家經(jīng)驗和相似產(chǎn)品的數(shù)據(jù)信息的特性，對產(chǎn)品各階段可靠性進行評估和預(yù)測.劉飛等人［8］將次序Dirichlet先驗分布的Bayes分析方法應(yīng)用到指數(shù)型產(chǎn)品的可靠性增長分析，并采用Gibbs抽樣得到Bayes區(qū)間估計.然而Li等人［9］指出次序Dirichlet分布在可靠性增長評估中的缺陷，并提出了基于新Dirichlet先驗分布的Bayes可靠性增長模型來避免這種缺陷，在每個增長評估階段都分別使用兩個參數(shù)描述階段可靠性的估計值和對估計值的確信程度.明志茂等人［10］基于新 Dirichlet先驗分布，利用Gibbs抽樣給出了多階段可靠性評估模型，并提出利用專家經(jīng)驗估計和最優(yōu)化方法給出先驗參數(shù)估計方法，但該先驗分布參數(shù)估計方法的主觀性比較強，健壯性不是很好.對于可靠性增長中的經(jīng)典AMSAA(Army Material System Analysis Activity)模型，Zhu等人［11］提出了 DGM-AMSAA 模型評估小子樣可靠性增長問題.邢云燕等人［12］利用離散AMSAA模型，由最大熵模型和矩相等的條件，給出Beta分布先驗參數(shù)估計，再結(jié)合現(xiàn)場試驗數(shù)據(jù)給出可靠度的Bayes估計，但該方法相對而言沒有充分利用上一階段的可靠性信息，并且對于離散AMSAA模型估計值的精確度影響也沒有足夠的討論.

基于上述模型的優(yōu)缺點，針對成敗型產(chǎn)品多階段可靠性增長的評估問題，本文提出了基于新Dirichlet先驗分布的Bayes評估模型.新Dirichlet先驗分布能夠充分利用上一階段的可靠性信息，在使用離散AMSAA模型獲得下一階段可靠性預(yù)測值為約束條件的情況下，利用最大熵模型，獲得先驗分布的參數(shù)估計.再結(jié)合現(xiàn)場試驗的數(shù)據(jù)，利用Bayes方法給出試驗之后的可靠性分析與評估.該方法能夠避免離散AMSAA模型的估計后驗可靠性的粗糙性，相較于基于Beta先驗分布和憑借專家經(jīng)驗獲得的參數(shù)估計，分布的最大熵模型更能考慮階段可靠性信息的運用，摒去主觀性對參數(shù)估計的影響，得到的結(jié)果更準確合理.

1 可靠性增長模型

新產(chǎn)品在研制過程中，由于設(shè)計上的潛在缺陷，必然反復(fù)地經(jīng)歷試驗—改進過程，以提高產(chǎn)品的可靠性，此過程稱為可靠性增長試驗(RGT，Reliability Growth Test).設(shè)RGT過程有m個階段，每階段試驗產(chǎn)品數(shù)為 n1，n2，…，nm，相對應(yīng)的失效次數(shù)為 f1，f2，…，fm.每階段試驗結(jié)束后，對故障進行修正改進，使得在新一階段的產(chǎn)品可靠性不斷增加.令第k階段的可靠度為Rk，則各階段的可靠度存在以下序化關(guān)系:

Bayes方法評估產(chǎn)品可靠性重要在于先驗分布的確定和參數(shù)的估計.文獻［7］中采用次序Dirichlet作為先驗分布，能較好地描述專家信息，但只用一個參數(shù)描述所有階段的方差卻并不合適.因此，Li等人［9］從一般的 Beta分布出發(fā)，提出用條件分布的形式描述可靠性增長.在第k階段未試驗前，構(gòu)造(Rk-1，1)上的截尾Beta分布作為該檢測區(qū)間內(nèi)產(chǎn)品可靠度的分布，稱為新Dirichlet分布，即有

新Dirichlet分布構(gòu)建在(Rk-1，1)之間，充分利用上一階段的可靠性評估結(jié)果，每個階段分別采用兩個參數(shù)，相較于次序Dirichlet分布使用一個參數(shù)來說，更能準確地描述專家經(jīng)驗信息，以及體現(xiàn)各個不同階段可靠性增長的變化，有更強的確信度.新Dirichlet分布在性質(zhì)與(0，1)上的標準Beta分布性質(zhì)類似.

在給定的Rk-1的條件下，求得Rk的均值和方差為

新Dirichlet先驗分布的后驗均值相較于Beta分布，增加了前一階段可靠度Rk-1的影響.若對Rk-1的大小進行變通，則其取值大小反映了對當(dāng)前可靠度估計值的不確定性和下一階段可靠度的預(yù)測，具有專家經(jīng)驗的指導(dǎo)意義.從新Dirichlet分布的特征來看，相對于次序Dirichlet分布，新的先驗分布的期望和方差的物理意義不是很明顯.若要應(yīng)用新Dirichlet先驗分布于可靠性增長的Bayes評估問題，必須先獲得先驗分布的參數(shù)估計.

2 新Dirichlet先驗分布的參數(shù)確定

文獻［10］利用專家經(jīng)驗給出每一階段可靠度估計值取值的區(qū)間范圍，再最優(yōu)化與均值和方差相關(guān)的函數(shù)來獲得先驗參數(shù).然而該方法中專家經(jīng)驗給出區(qū)間均值和方差的不同會導(dǎo)致不同的參數(shù)估計，主觀性對參數(shù)估計的結(jié)果影響較大，因此，為能夠摒棄主觀性對于參數(shù)估計的影響，采用基于最大熵原理的參數(shù)估計方法來獲得先驗分布參數(shù)估計.在信息論中，熵是不確定性的一種度量［13］.在無信息或信息很少的情況下，用最大熵來確定先驗分布，就是采取一種保守的方法.新Dirichlet先驗分布已經(jīng)充分包含之前有的可靠性信息，因此基于最大熵原理的參數(shù)估計方法是可信的.

先驗分布π(Rk)的熵可以表示為

若要求得先驗分布的參數(shù)估計，必須給出關(guān)于下一階段可靠性Rk的相關(guān)信息，例如均值或者分位值等信息.本文假設(shè)在給出關(guān)于Rk的期望均值估計的條件下，通過極大化下列模型得到參數(shù)估計:

由于新Dirichlet分布的形式比較復(fù)雜，可借助計算軟件搜索最大熵的估計值.對于下一階段可靠性的估計R^k，可以通過專家經(jīng)驗給出，為了減少主觀性對參數(shù)估計的影響，本文采用離散AMSAA模型求得可靠性估計值R^k.

3 離散AMSAA模型

文獻［14］在對各種產(chǎn)品的失效數(shù)據(jù)進行統(tǒng)計分析時，提出一個近似函數(shù)關(guān)系式來描述失效數(shù)據(jù)與失效時間之間的關(guān)系，即學(xué)習(xí)曲線特性:其中，λ為該函數(shù)形狀參數(shù)，β為尺寸參數(shù)，均為正值;T為累計的試驗時間;函數(shù)K(T)表示到時間T時觀測到的累計失效次數(shù).

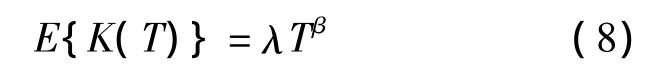
如果將式(8)中的累計試驗時間T改為累計試驗次數(shù)N，使其離散化，便可以得到離散型學(xué)習(xí)曲線特性［15］:

則每一試驗階段失效次數(shù)為

如此，每一階段的可靠度為

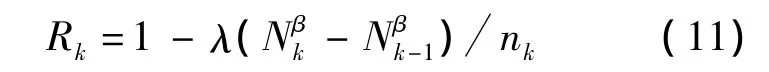
其中，nk=Nk-Nk-1，表示第k階段的試驗樣本數(shù);λ為初始階段可靠性，0＜λ＜1;1-β為增長率，0＜β＜1.

模型假設(shè)改正措施是在試驗結(jié)束之后進行，并且試驗中發(fā)生失敗次數(shù)為隨機數(shù).

對于模型中的參數(shù)求解，可借助于極大似然函數(shù)獲得:

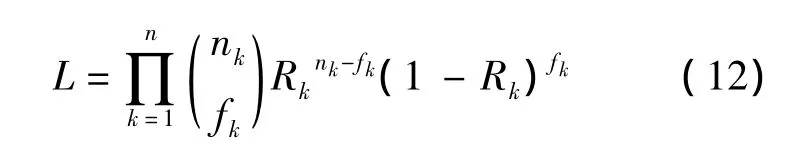
其中，fk表示在第k階段失效次數(shù);n表示試驗的階段數(shù).

已知第k階段的試驗樣本量nk，利用式(12)得到參數(shù)估計值和，則第k階段的可靠性估計值為

4 可靠性Bayes估計

設(shè)在第k階段的可靠性現(xiàn)場試驗中，試驗數(shù)據(jù)為(nk，fk)，則現(xiàn)場試驗數(shù)據(jù)的似然函數(shù)為

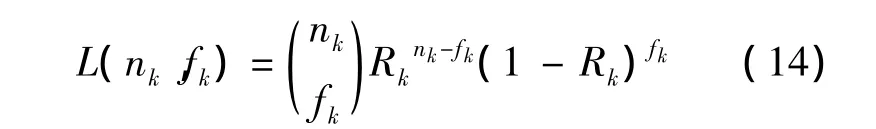
其中，nk為試驗次數(shù);fk為試驗中失敗次數(shù).

先驗分布的參數(shù)估計通過AMSAA模型和最大熵模型得到.由于新Dirichlet分布的性質(zhì)與Beta分布的性質(zhì)相似，那么根據(jù)Bayes原理，結(jié)合現(xiàn)場試驗數(shù)據(jù)得到可靠性后驗分布為

5 實例分析

某成敗型產(chǎn)品研制試驗采用延緩糾正方式，已經(jīng)歷4階段的可靠性試驗.其中，第1階段試驗4次，失敗2次;第2階段試驗5次，失敗2次;第3階段試驗5次，失敗1次;第4階段試驗4次，全部成功.根據(jù)上述試驗數(shù)據(jù)，分析此時試驗結(jié)束時的產(chǎn)品可靠性是否滿足要求(可靠度為0.9).

根據(jù)已有的4階段試驗信息，基于Laplace檢驗統(tǒng)計量進行可靠性增長趨勢檢驗.結(jié)果表明當(dāng)顯著性α=0.2時，μ=-1.3771＜μα=1.282，可靠性有明顯的增長趨勢.由式(12)，得到離散AMSAA模型參數(shù)的極大似然估計，=0.988 4，β^=0.5588.根據(jù)式(13)得到第3階段可靠度估計=0.811，第4 階段可靠度估計=0.837.然而，根據(jù)第3階段和第4階段的試驗信息，可以粗略判斷后驗可靠度至少在90%以上，顯而易見離散AMSAA模型對于下一階段可靠度的估計精度并不十分準確.本文采用基于新Dirichlet先驗分布的Bayes方法估計試驗結(jié)束后的可靠性.

將AMSAA模型估計得到的第3階段可靠性作為起點，在區(qū)間(Rk-1，1)上構(gòu)建新Dirichlet先驗分布.以第4階段可靠性估計值作為均值約束，利用式(7)的最大熵模型獲得參數(shù)的估計.然而由于兩階段可靠性估計值相近，導(dǎo)致最大熵模型求解先驗參數(shù)無解.由于離散AMSAA模型對下一階段參數(shù)估計的不準確，為了校正模型故取0.9Rk-1代替 Rk-1，由式(16)得到最終可靠度的Bayes后驗期望為=0.938，可信度為90%時對應(yīng)的可信下限R0.9=0.7424.

從離散AMSAA模型在給出下一階段的可靠度估計值上看，僅憑離散AMSAA模型估計后驗可靠性可能會存在明顯誤差.如果對離散AMSAA模型獲得的下一階段可靠度估計值的區(qū)間范圍存在準確度的疑慮，從而導(dǎo)致在區(qū)間(Rk-1，1)上給出的可靠度后驗估計值增大的情況，可以選取一個校正系數(shù)c∈(0，1)，作為對估計值R^k-1的信任度，c越趨近于1表明對R^k-1估計值的確信度越大，從而用(cRk-1，1)代替(Rk-1，1)進行該階段的新Dirichlet先驗分布的構(gòu)建.由式(16)可知，該階段的后驗期望有隨著c減小而減小的趨勢，說明c的大小也是對最終后驗可靠度估計值的確信度大小的表示，c越小表明對后驗估計得越趨向于保守.表1列出了不同c值時該階段的后驗可靠度的估計值.從結(jié)果分析上看，當(dāng)c的取值低于某一值時，該階段的先驗參數(shù)b的估計值相同，變化的是先驗參數(shù)a的值，經(jīng)過大量仿真試驗也發(fā)現(xiàn)類似情況，導(dǎo)致上一階段可靠度估計對后驗可靠度估計影響減弱，估計結(jié)果趨向于Beta分布估計，證明了常數(shù) c在可靠性估計中的作用.新Dirichlet先驗分布的估計結(jié)果與Beta先驗分布相比較，Beta先驗分布略顯保守，是因為沒有充分利用每一階段的可靠度信息，因此更能突出新Dirichlet先驗分布的優(yōu)勢.

表1 不同c值對應(yīng)的可靠度后驗估計Table 1 Reliability posterior estimation corresponding to different value of c

然而通常離散AMSAA模型對當(dāng)前可靠度的估計準確度還是比較可信的，但若得到的下一階段可靠度估計值明顯不準確，則需要根據(jù)專家經(jīng)驗對可靠度估計值進行修正.表2列出了對下一階段可靠度估計值進行修正后的后驗可靠度的變化.從表2結(jié)果對比中可以看出，給出先驗信息越高時，獲得的后驗估計也就越大，因此對于先驗信息的修正也反映出專家經(jīng)驗對于產(chǎn)品可靠度的判斷.從兩表對比可以看出，對于下一階段可靠度估計值的修正對后驗可靠度的影響，要大于對上一階段可靠度估計區(qū)間修正的影響.適當(dāng)利用專家經(jīng)驗，可以使得評估結(jié)果更優(yōu).

表2 不同先驗信息對后驗可靠度的影響Table 2 Impact of different prior information on the posterior reliability estimation

從表1、表2的評估結(jié)果分析可以看出，在離散AMSAA模型給出的可靠度估計不甚理想時，如當(dāng)利用離散AMSAA模型估計得到的下一階段可靠度的估計值與當(dāng)前階段估計值相近時，或者離散AMSAA模型對當(dāng)前階段和下一階段的可靠性估計同時出現(xiàn)誤差較大時，可能會導(dǎo)致利用最大熵模型時不能獲得先驗參數(shù)估計.此時后驗可靠度的大小可以通過專家經(jīng)驗對于下一階段可靠度估計的準確性和取值范圍的確信度的判斷對模型進行修正.因此，基于新Dirichlet先驗分布的Bayes估計方法能夠較好地融合專家經(jīng)驗和上一階段的可靠度信息，比單純運用離散AMSAA模型估計下一階段可靠性要準確得多.

6 結(jié)論

1)針對成敗型系統(tǒng)的可靠性增長問題，在結(jié)合離散 AMSAA模型的基礎(chǔ)上，提出了基于新Dirichlet先驗分布的評估模型.該模型能夠充分利用各階段的可靠性信息，在合適的專家經(jīng)驗指導(dǎo)下，能夠較為準確地得到系統(tǒng)增長后的可靠性.

2)該模型評估系統(tǒng)增長后的可靠性的精度與專家經(jīng)驗有關(guān)，在對當(dāng)前階段的可靠度無法給出恰當(dāng)?shù)墓烙嫊r，該模型可以退化成Beta分布，具有一定的靈活性.

3)相較于傳統(tǒng)模型中采用的積分模型，該模型的計算過程較為簡便，避免復(fù)雜的積分問題，能夠保證計算結(jié)果的準確性.

然而，該模型還存在一些問題.

1)當(dāng)離散AMSAA模型對上一階段可靠性的估計存在明顯偏差時，利用校正系數(shù)進行校正時，該系數(shù)選取值的大小存在主觀性.如何給出校正系數(shù)客觀公正的選取規(guī)則，是需要研究的問題.

2)上一階段可靠性估計不準確也可能會導(dǎo)致利用最大熵模型得不到先驗分布的參數(shù)，此時同樣需要借助校正系數(shù)進行改進.在選取校正系數(shù)時，也需要同時考慮極大熵模型的影響.

References)

［1］ Smith A F M.A Bayesian note on reliability growth during a development testing program［J］.IEEE Transactions on Reliability，1977，R-26(5):346-347

［2］ Barlow R E，Scheuer E M.Reliability growth during a development testing program［J］.Technometrics，1966(8):53-60

［3］ Sohn S Y.Bayesian dynamic forecasting for attribute reliability［J］.Computer＆ Industrial Engineering，1997，33(3/4):741-744

［4］田國梁.二項分布的可靠性增長模型［J］.宇航學(xué)報，1992(1):55-61 Tian Guoliang.Reliability growth models for binomial distribution［J］.Journal of Astronautics，1992(1):55-61(in Chinese)

［5］ McLaren A E.A method for reliability growth analysis combined over multiple stages［D］.West Lafayette:Purdue University，2011

［6］ Nicholls J L.Reliability growth of multi-stage single shot systems［D］.Washington D C:The George Washington University，2011

［7］ Mazzuchi T A，Soyer R.A Bayesian attribute reliability growth model［C］//Proceedings of the Annual Reliability and Maintainability Symposium.Piscataway，NJ:IEEE，1991:322-325

［8］劉飛，王中偉，張為華.指數(shù)壽命產(chǎn)品可靠性增長試驗的Bayes分析［J］.國防科技大學(xué)學(xué)報，2006，28(4):128-132 Liu Fei，Wang Zhongwei，Zhang Weihua.Bayesian analysis of reliability-growth test for exponetial life distribution case［J］.Journal of National University of Defense Technology，2006，28(4):128-132(in Chinese)

［9］ Li G Y，Wu Q G，Zhao Y H.On Bayesian analysis of binomial reliability growth［J］.J Japan Statist Soc，2002，32(1):1-14

［10］明志茂，張云安，陶俊勇，等.基于新Dirichlet先驗分布的指數(shù)壽命型產(chǎn)品多階段可靠性增長Bayes分析［J］.兵工學(xué)報，2009，20(6):733-739 Ming Zhimao，Zhang Yun'an，Tao Junyong，et al.Multi-stage reliability growth bayes analysis for exponential product based on new Dirichlet prior distribution［J］.Journal of Acta Armamentarii，2009，20(6):733-739(in Chinese)

［11］ Zhu X，F(xiàn)ang Z.“DGM-AMSAA”model of reliability growth based on the small sample［C］//2013 IEEE International Conference on Grey Systems and Intelligent Services.Piscataway，NJ:IEEE，2013:123-126

［12］邢云燕，武小悅.成敗型系統(tǒng)可靠性增長的動態(tài)Bayes評定方法［J］.系統(tǒng)工程理論與實踐，2010(4):695-699 Xing Yunyan，Wu Xiaoyue.Dynamic Bayesian evaluation method for binomial system with reliability growth［J］.Journal of Systems Engineering-theory ＆ Practice，2010(4):695-699(in Chinese)

［13］ Berger J O.Statistical decision theory and Bayesian analysis［M］.Heidelberger:Springer，1985

［14］ Fries A，Sen A.A survey of discrete reliability-growth models［J］.IEEE Transactions on Reliability，1996，45(4):582-604

［15］ Fries A.Discrete reliability-growth models based on a learningcurve property［J］.IEEE Transactions on Reliability，1993，42(2):303-306