金屬管件受沖擊時的數值模擬和屈曲分析＊

楊彬彬 趙修平 王兆軍

（1．海軍航空工程學院 煙臺 264001）（2．92095部隊 臺州 318000）

1 引言

在現代戰爭中，武器裝備除了要執行自己的作戰任務外，不可避免的要面對來自敵方的威脅［1～2］。所以，在戰場上，我方武器裝備的生存能力，也是武器裝備設計時所必須要考慮到的因素。

不論是飛機、卡車還是艦艇上，都存在著燃料和水等液體的存貯和輸送設備，而細長的輸送管道也滿面暴露在外，或者是安放在防護層較弱的地方。它們承載著裝備的生命動力，是裝備發揮其作戰效能的根本保證［3］。與此同時，這些設備又是最容易受到打擊、最容易被破壞的部分。試想，一輛汽車的油箱著火已經足夠威脅全車人的生命安全，更何況飛機和艦艇［4］。

在實際戰爭中，當炮彈在設備附近爆炸時，產生的破片幾乎可以覆蓋各個角度，也就不可避免地會飛濺到油箱、水箱及其輸送管道上。所以，本文以此為背景，分析不同形狀的破片或子彈等沖擊體，對貯液管件沖擊碰撞時產生的影響。這對今后武器系統的設計優化有著重要的意義［5～12］。

2 碰撞有限元理論

碰撞過程是一個瞬態的大位移和大變形的力學過程，接觸和沖擊載荷影響著整個碰撞過程，且具有幾何非線性和材料非線性等多重非線性的特點［7］。嚴格地說，實際的工程問題都是非線性的，在計算時，常常把非線性的問題理想化，很多時候也能滿足工程要求。隨著高速計算機和各類仿真軟件的發展，對于沖擊碰撞過程中產生的大變形問題，可以通過在計算機的輔助下運用有限元算法加以解決。ANSYS／LS-DYNA［13～15］是一個非線性顯式有限元程序，其算法基于以下方程：

1）能量方程

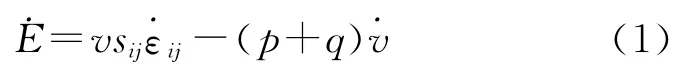
2）動量方程

式中，σij為柯西應力；fi為單位質量體積力；為加速度。

3）質量守恒方程

式中，v為相對體積；ρ為當前質量密度；ρ0為初始質量密度。

4）邊界條件

實際結構的大變形碰撞問題的邊界條件包括面力、位移和接觸條件。

（1）力邊界條件

式中，nj為現實構形邊界的外法線方向余弦；ti為面力載荷。

（2）位移邊界條件

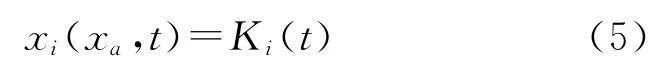
式中，xa為t＝0時候的位移；Ki（t）（t＝1，2，3）為給定位移函數。

對于上述偏微分方程和相應的定解條件，由于方程的非線性性質和邊界條件的復雜性，一般不能用解析方法求出精確解。

采用有限元方法求解上述偏微分方程和相應的定解條件，其伽遼金弱形式的平衡方程為：

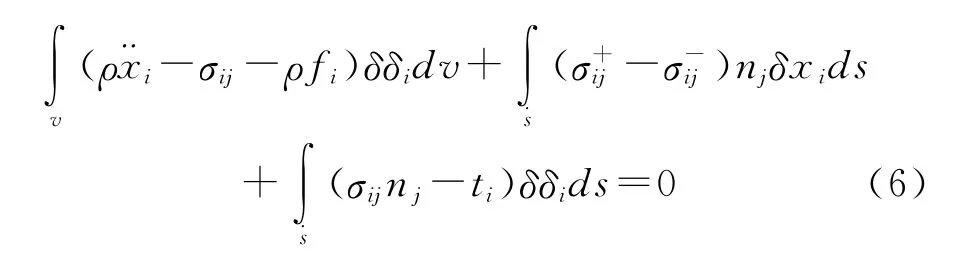
應用散度定理，得到：

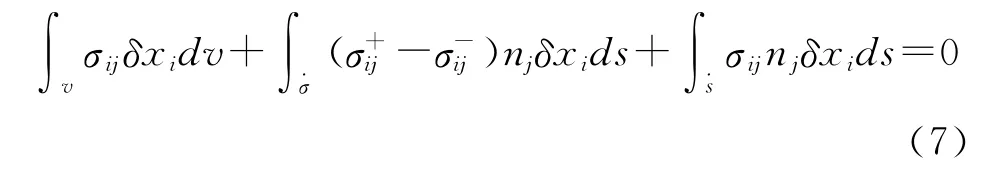
運用分步積分σijδxi-σijδxi＝σijδxi，于是，伽遼金弱形式的平衡方程就可以得到：

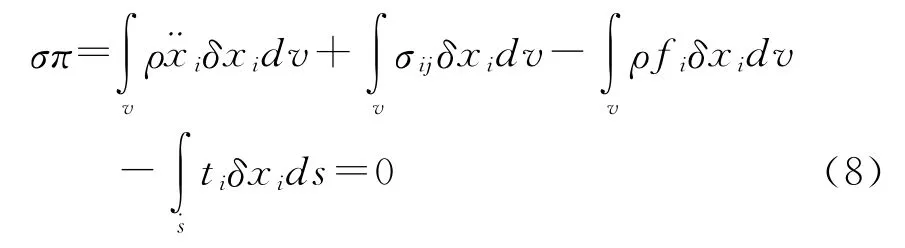
上式經過單元離散后，就可以得到有限元法求解變形碰撞的非線性分析的運動方程：

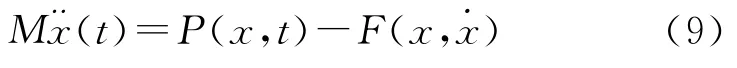
其中，

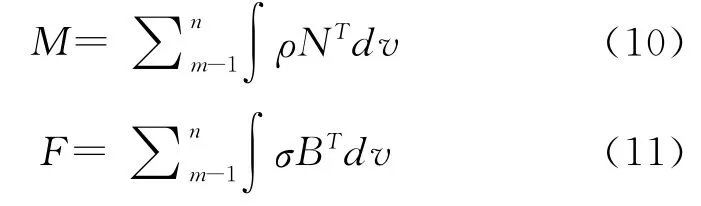
式中，M為總體質量矩陣；（t）為總體結點加速度向量；P為總體載荷向量，由結點載荷、面力、體力等形成；F為單元應力場的等效結點力向量組集而成；N為形函數矩陣；B為應變矩陣；σ為應力向量。

3 有限元模型的建立

建立沖擊體與金屬管件沖擊碰撞有限元模型，必須先建立其幾何模型，幾何模型建立的準確與否、簡化的合理與否將直接影響分析的結果。

根據板殼理論，在圓筒殼上作用集中載荷時，最大應力主要集中在作用點附近，其他部位幾乎不受影響。所以，在幾何模型的建立上，我們截取金屬管的一段進行研究。

假設，質量為M、長為L的薄壁金屬圓柱殼，在沖擊點受到以初速度v運動的、質量為m的沖擊體撞擊。碰撞時，圓柱殼產生塑形動力響應。在碰撞瞬時，金屬殼在沖擊點處也以初速度v運動，而金屬殼的其余部分則處于靜止狀態。也就是說，擾動是從沖擊點處開始向四周進行傳播。這里假定沖擊體始終與金屬殼保持接觸。

圖1 沖擊體與金屬管件有限元模型

模型中，金屬管的有限元模型尺寸為，長L＝200mm，直徑D＝50mm，壁厚t＝1．0mm。為了使沖擊效果更加明顯，把沖擊體設計成為子彈形狀的椎體。在這里采用了三種彈頭（形狀分別為圓柱形、方形和球形）對模型進行分析。沖擊體尺寸為長l＝60mm，直徑或邊長d＝10mm，質量約為m＝0．5kg。其結構如圖2所示。

模型建立好以后，下一步是對其進行有限元網格劃分。采用的是映射網格的方法，此方法通常包含較少的單元數量，對單元的形狀有限制。在有限元模型，金屬管采用SHELL163的4節點單元，網格尺寸為0．02mm 左右；沖擊體采用SOLID164單元，網格尺寸為1mm 左右。

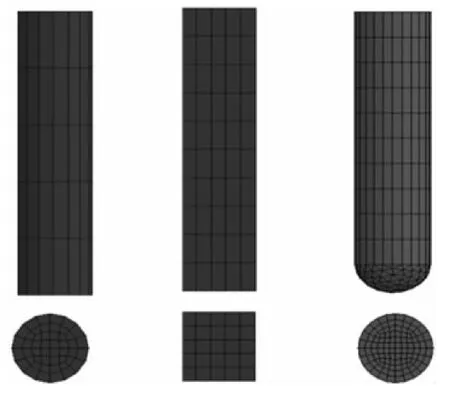
圖2 圓柱形、方形和球形沖擊體

材料方面，彈體采用不變形的剛體（rigid）材料模型，材料為鋁AA 6060T4。圓柱殼中填充的液體，分別為液體為水和工業液壓油。其中液體采用流體（Fluid）材料模型，液體的單元類型為SOLID164單元。材料參數如表1所示。

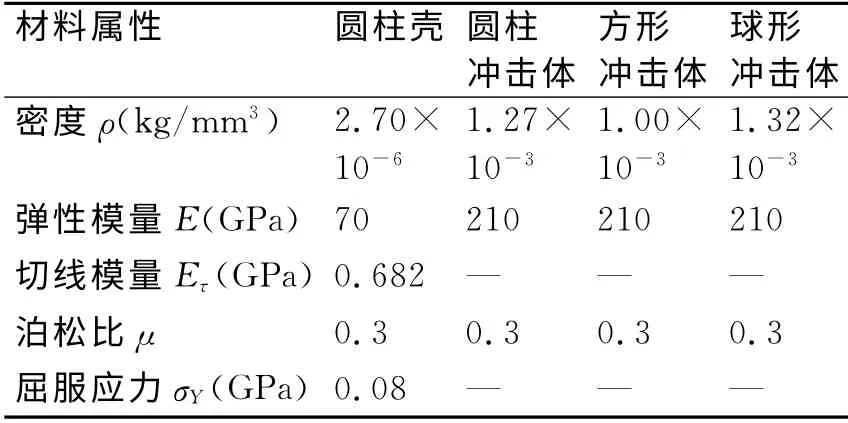
表1 薄壁圓柱殼及子彈的材料屬性

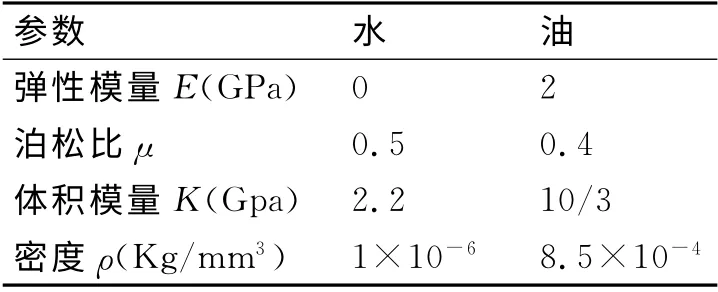
表2 充液圓柱殼中內充物的材料屬性

接觸類型和邊界條件方面，子彈沖擊充液圓柱殼共設定兩種接觸算法：自動單面接觸（ASSC）、自動面-面接觸（ASTS）。對圓柱殼定義自動單面接觸；對子彈和圓柱殼之間定義自動面-面接觸；對圓柱殼和液體之間定義自動面-面接觸。薄壁圓柱殼和液體的邊界條件為兩端固定，子彈僅在沖擊方向以v＝10m／s的速度運動，其他方向的自由度全部固定。

4 ANSYS仿真結果

根據建立的有限元模型，運用ANSYS對其受力過程和能量吸收過程進行有限元分析。對于不同類型的內充物，在不同形狀的沖擊體作用下的時間-能量吸收曲線圖。

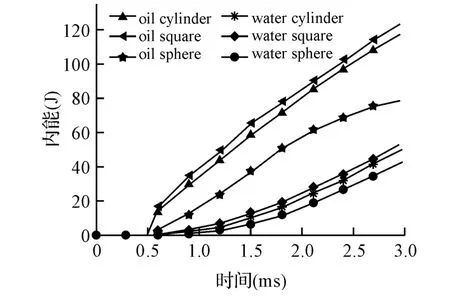
圖3 不同內充物的圓柱殼在不同形狀子彈的沖擊下的時間-能量吸收曲線圖

在同樣的條件下，分別對每一種形狀的從沖擊體進行接觸力的分析，得到時間-接觸力曲線圖。

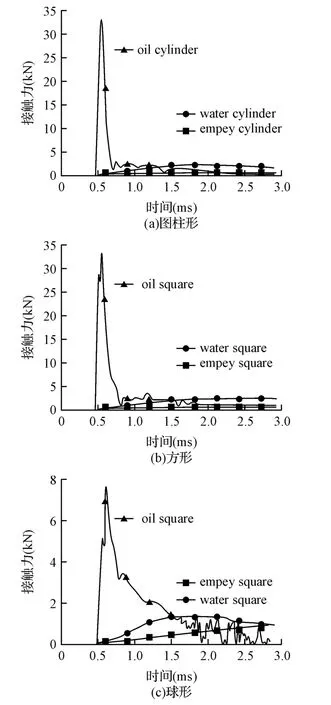
圖4 不同圓柱殼在不同形狀沖擊體作用下的時間-接觸力曲線圖

5 結語

根據仿真結果，不難看出：

1）在圓柱殼內充物相同的情況下：從“時間-能量吸收”曲線可以看出，方形沖擊體作用時金屬殼吸收的能量最大，球形的能量最小，而圓柱形居中。而對于受力方面，從“時間-接觸力”曲線得出，對于不同形狀的沖擊體對圓柱殼接觸力的影響極大。方形和圓柱形沖擊體作用時金屬殼產生的作用力峰值遠遠大于球形沖擊體作用時的峰值。

2）在沖擊體形狀相同的情況下：因為油的密度大于水，所以可以得出，金屬殼內的填充液體的密度越大，外殼在遭受沖擊時所吸收的能量越多。而對于受力方面，密度越大的填充物使得所受沖擊力的峰值越大，在這里可以看出，充油時的峰值要遠遠高于充水的情況。

3）當圓柱殼內充物的密度越大時，沖擊體形狀的變化對殼吸能情況的影響越明顯。同時，密度越大時，“時間-接觸力”曲線初始峰值越高，可見，金屬殼內的液體密度越大時，受到沖擊體作用時會產生強烈的震蕩。

［1］杜星文，宋宏偉．圓柱殼沖擊動力學及耐撞性設計［M］．北京：北京科學出版社，1999．

［2］路國運，程國強，雷建平，等．充液圓柱殼軸向沖擊屈曲的計算機仿真分析［J］．太原理工大學學報，1999，30（6）：555-558

［3］Jones N．結構沖擊［M］．蔣平，譯．成都：四川教育出版社，1994．

［4］B．T．利津，B．A．皮亞特金．薄壁結構設計［M］．廖啟端，譯．北京：國防工業出版社，1994．

［5］Jones N．Recent progress in the dynamic plastic behaviour of structures［J］．J．Appl．Mech．Rew．，1989，42（2）：95-115．

［6］Zhang S Y，Jianping Lei，Longmao Zhao，et al．Experimental investigation and computer simulation on dynamic buckling behavior of liquid-filled cylindrical shells under axial impact［J］．Acta Mechanica Solida Sinica，2000，13（2）：166-172．

［7］翁智遠，王遠功．彈性薄殼理論［M］．北京：高等教育出版社，1987．

［8］Wang L，Yang L，Huang D．An impact dynamics analysis on a new crashworthy device againstship-bridge collision［J］．International Journal of Impact Engineering，2008，35（8）：895-904．

［9］雷正保．大變形結構的耐撞性［D］．長沙：中南大學，2004．

［10］BISAGNI C．Crashworthiness of helicopter subfloor structures［J］．International Journalof Impact Engineering，2002，27（10）：1067-1082．

［11］HEIMBS S．Computational methods for bird strike simulations：Areview［J］．Computers kStructures，2011，89（23-24）：2093-2112．

［12］葛樹文，崔國華，馬若丁．基于能量吸收控制的工程車輛傾翻保護結構設計方法［J］煤炭學報，2008，33（1）：111-115．

［13］尚曉江，蘇建宇．ANSYS／LS-DYNA 動力分析方法與工程實例［M］．北京：中國水利水電出版社，2006．

［14］HALLQUIST J 0．LS-DYNA theory manual［M］．California：Livermore Software Technology Corporation，2006．

［15］趙海鷗．LS-DYNA 動力分析指南［M］．北京：兵器工業出版社，2003．