基于二分圖的艦艇編隊網絡故障定位方法＊

（92493部隊98分隊 葫蘆島 125000）

1 引言

造成艦艇編隊網絡不穩定的原因很多，但很大程度上是因為故障處理不夠及時或對故障處理反應過于強烈造成的。當故障發生后，網絡系統通常需要在全網絡進行大規模故障信息通告，這種通告不僅會造成鏈路負載的增加，也會使節點因頻繁處理故障信息而出現網絡振蕩的現象，影響了網絡的穩定性［1］。

網絡故障定位是根據觀察到的故障癥狀信息推理出故障所在位置的過程。作為故障診斷中最為復雜和耗時的環節，其效果和效率對于后期的故障排除至關重要。而早期故障診斷主要是靠專家來通過人工完成，但是目前網絡系統的規模不斷擴大及網絡復雜性的增加，人工的診斷方法已經不能適應需求。因此需要研究與開發一套可以智能地進行網絡故障診斷的技術［2］。

2 將故障診斷轉化成0-1規劃問題

在進行故障診斷時，我們把實際所觀察到的發生故障的集合用故障S的子集C來表示，C中沒有包含的故障就認為是沒有發生［3］。為便于對網絡的故障診斷進行研究，在此提出如下假設：

1）假定各故障之間相互無依賴關系，彼此互不影響；

2）假定事件和故障間因果映射的強度固定不變。也就是說，不論故障ti是否發生或者何時發生，事件ci總能以相同的概率強度發生。

通過基于二分圖的故障診斷，從候選的故障集合T內找出故障假設X?T，使得此故障假設能夠發生的概率最大，即

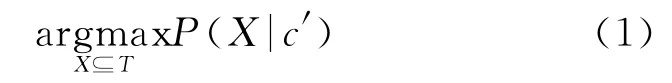
式中c′代表網絡中能夠觀察到的事件的集合。由貝葉斯公式可得：

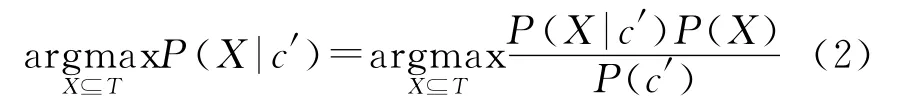
為了可以突出地描述問題，本文定義了一個k維的向量。其中k表示網絡中的所有可能出現的故障個數，每個故障ti與故障假設X之間存在著以下關系：

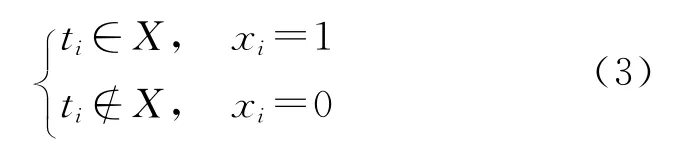
因為P（c′）為常數，所以求式（2）的最大值問題就變為求式（4）的最大值問題。

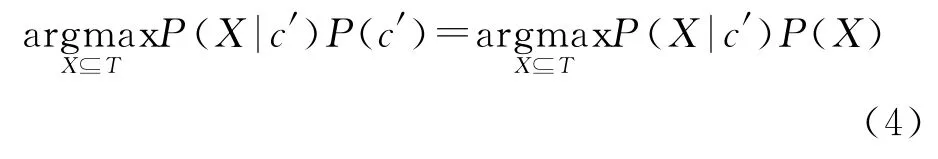
在基于二分圖的網絡故障模型里有：

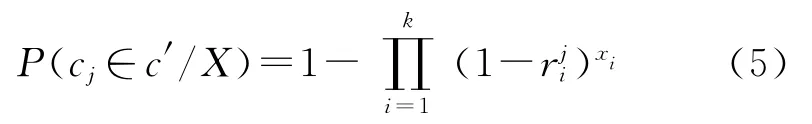
綜合式（1）～式（5），就可得到基于二分圖的網絡故障診斷問題最后的目標函數：

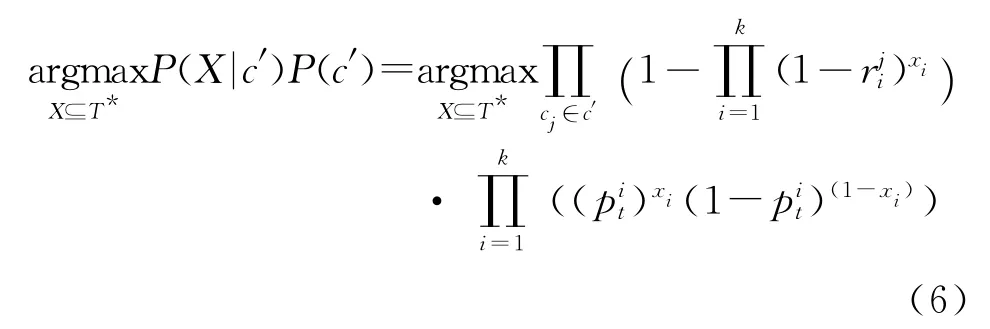
式中T＊表示故障集合T減掉與觀察事件所對應故障集合T′的值，即T′＝T-T＊。根據故障診斷和定位的原理，對每一個觀察事件ci而言，其最優解中應至少含有一個故障ti，即當＞0時，有故障ti存在。因此，在網絡的故障診斷中，對每一個能夠觀察到的事件，其結果中一定至少存在一個故障與之對應。假設矩陣B是由關聯矩陣所得到的一個結果矩陣，其中，矩陣每一行代表一個事件ci所對應故障，即這些故障將一定會

式中，代表一個維的列向量。將式（4）取對數，就可以得到式（8）。

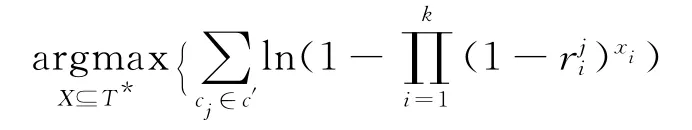
因此，可以將網絡故障的診斷問題轉化成以下的最小化求解問題：

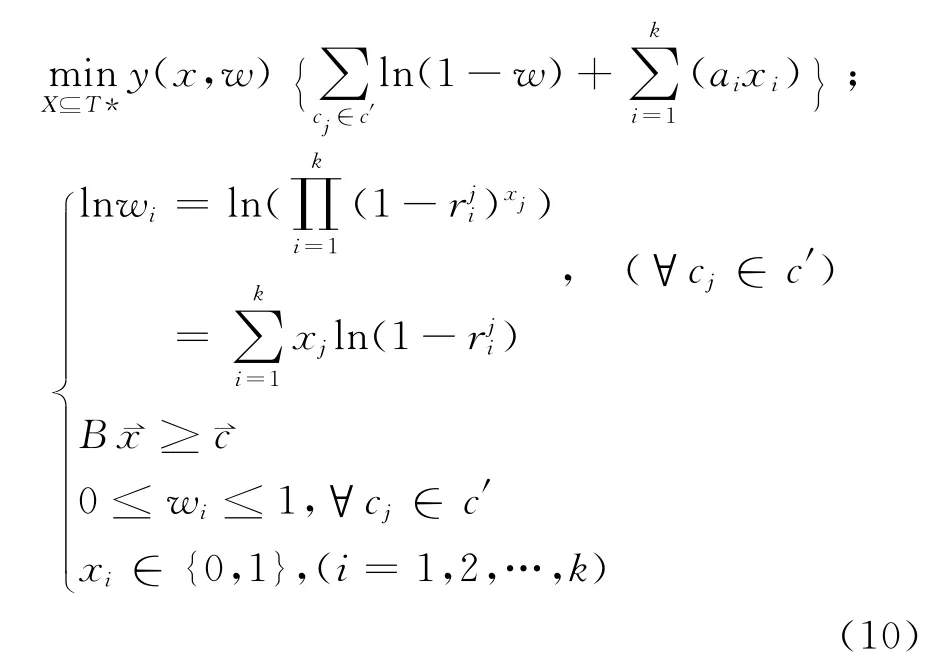
從式（10）能夠得出網絡故障的診斷問題在實質上就是一個求解0-1最優化的問題。通常0-1規劃問題采用窮舉法來求解，另外也有分枝定界方法及拉格朗日方法等。其中，分支定界求法是特殊的一種隱枚舉方法，但是故障診斷中，目標的松弛下界不易求解，因此該方法計算量很大。因此，本文采用基于免疫遺傳進化的算法來求解此最優化問題。

3 基于免疫遺傳算法的定位方法求解

算法的總體思路為：為增強種群動態環境下探索的力度，在遺傳的同時引進了雜合映射的思想來防止種群進化信息出現停滯。為了使個體能夠對故障進行更快響應，在檢測到系統可能發生故障時，將有價值的原記憶信息重新進行激活。將和故障狀態最能夠相匹配的個體遺傳和變異，一方面擴大搜索的空間，另一方面兼顧尋找最優解速度。從而使種群可以更快地追蹤系統的狀態變化。

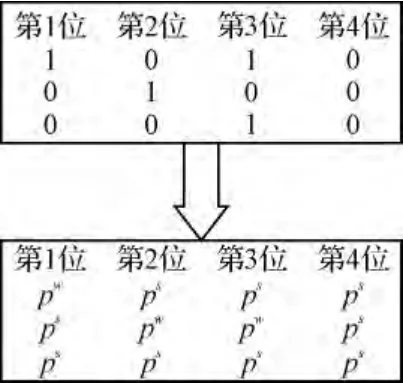
圖1 映射機制舉例

假定在t代種群中進行遺傳的個體數目以概率pd進行選擇［6］。將數目較少的基因座的值叫做該基因座的弱勢基因值，反之稱為強勢基因值。按照雜合子的原理，通過適應性地調整強弱勢基因值的數量來對基因的突變概率進行控制。用與來分別代表弱勢基因值與強勢基因值間映射的概率。映射關系舉例如圖1所示。

與的計算過程為：

1）設種群數目是NP，編碼長度是L。Ⅰk（t）代表第t代個體中第k個基因座的弱勢基因值的期望個數，用γk（t）、ηk（t）分別代表非遺傳個體與遺傳個體中的第k個基因值是弱勢基因值的個體數目，從而得到

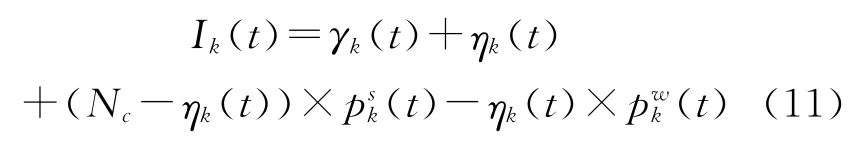
令ND≤NP／2，則由（t）∈［0，1］得

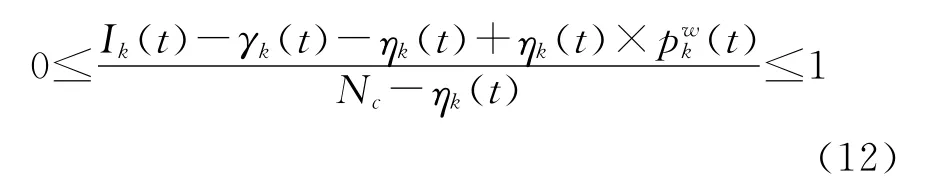
2）對其分兩種情況進行討論：

（1）當Nc＝ηk（t），（t）＝（t）＝0時，染色體上的基因座都是弱勢基因值，不進行運算。

（2）當Nc＞ηk（t）時，若ηk（t）＝0，則染色體的第k位上不存在弱勢基因，因此（t）＝若ηk（t）＞0則有

此不等式能夠成立的邊界條件為γk（t）≤ηk（t）≤γk（t）＋Nc。根據式（11）可知，γk（t）＋ηk（t）＜Ⅰk（t）。由上式可取（t）＝min，1）×ε，其中ε∈［0，1］。相反，則有（t）＝（t）＝0。基于免疫遺傳算法的故障定位方法的步驟如圖2所示。

4 算法的性能測試與結果分析

按照式（10）產生模板T，然后將其與目標串（第t代個體）X做“異或”（“⊕”）運算，異或運算的規則為0⊕0＝0，0⊕1＝1，1⊕1＝0。若在模板T中的某一位值是1，則進行位運算操作后，目標串X的相應位就發生變化（由0變為1，或由1變為0）。而模板的位值是0時，目標串X中相應的位則會保持不變。因此，可將T的位值是1的位和模板的長度之比看作是故障率的大小。下面定義幾個參數：

設網絡Ni中隨機產生鏈路故障數為，故障集為Wi，故障的定位結果為?Wi。故障檢測率誤檢率

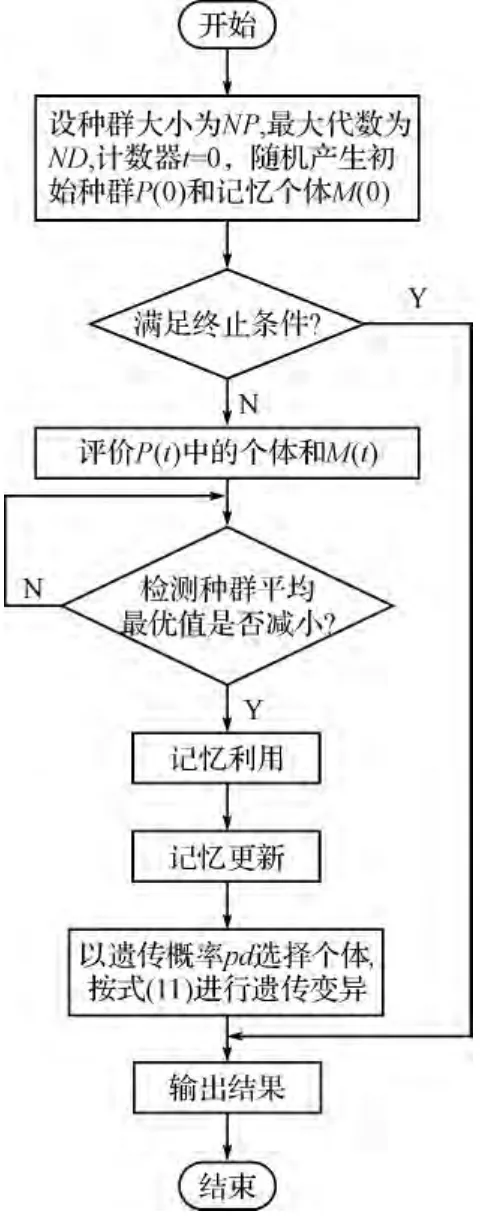
圖2 基于免疫遺傳算法的故障定位方法設計步驟

在仿真中，本文所提的算法與IHU（Incremental Hypothesis Updating）算法和窮舉法作對比，分別得到了TP、FP及故障診斷時間T的值。仿真的結果如圖3所示。

圖3 仿真結果

從圖3可以看出，隨著網絡節點數的增加，網絡規模的擴大，三種方法的性能都有所降低，其中窮舉法由于在網絡規模增大情況下復雜性的增加而性能迅速降低，但是從總體上來說，免疫遺傳定位法的性能始終優于其余兩種方法。免疫遺傳算法的故障定位檢測率始終保持在0．95以上，誤檢率能保持在0．02以下，這與基于免疫遺傳算法的數據計算準確性有關，故障定位時間與IHU 算法相差不大，但明顯低于窮舉法。

5 結語

本文提出了基于免疫遺傳算法的故障定位機制，仿真結果表明其有效性良好。尤其當網絡規模較大或適中時，其優勢則體現更加明顯。這主要因為當網絡規模較大時，歷史的記憶信息可對相似網絡狀況下的網絡尋優有很好的指導意義。

［1］Liu L L，Wang D W，Ip W H．A permutation-based dual genetic algorithm for dynamic optimization problems［J］．Soft Computing，2008，13（7）：725-738．

［2］Howard F．Lipson，David A．Fisher．Survivability-A New Technical and Business Perspective on Security［C］／／Proceedings of the New Security Paradigms Workshop，1999：76-81．

［3］Nancy R．Mead，Robert J．Ellison．Survivable Net-work Analysis Method［EB／OL］．http：／／www．cert．org／archive／pdf／00tr013．pdf，2000．

［4］Harmer P K，Williams P D，Gunsch G H，et al．An artificial immune system architecture for computer security applications［J］．IEEE Transactions on Evolutionary Computation，2002，6（3）：252-280．

［5］Hong Zheng，Jingxin Zhang，Saeid Nahavandi．Learning to detect objects by artificial immune approaches［J］．Future Genaration Computer Systems，2004，20：1197-1198．

［6］楊嬌．二分圖網絡故障傳播模型與故障診斷算法研究［D］．沈陽：東北大學，2010，12：22-40．

［7］王洪峰，汪定偉，楊圣祥．動態環境中的進化算法［J］．控制與決策，2007，22（2）：127-131．

［8］劉黎黎，汪定偉．基于雜合機制的免疫遺傳算法在動態問題中的應用［J］．控制與決策，2009，12（24）：1841-1845．

［9］Zhang Q．Probabilistic Reasoning based on Dynamic Causality Tree Diagrams［J］．Reliability Engineering and System Safety，1994，46：209-220．

［10］Garza C L，Pablo N J，Garza C M，et al．Fault diagnosis of industrial systems with Bayesian networks and neural networks［J］．Computer Science，2008，5317（11）：998-1008．

［11］Li Qing，Xu J Z．Power system fault diagnosis based on subjective Bayesian approach［J］．Automation of Electric Power Systems，2007，31（15）：46-50．