障礙物環境下的動態單純型連續近鄰鏈查詢

李 松，張麗平，劉 艷，郝曉紅，楊和禹

(哈爾濱理工大學a.計算機科學與技術學院;b.計算中心，哈爾濱 150080)

1 概述

數據集中的近鄰查詢問題在空間數據庫、海量數據查詢與分析、大數據處理、數據挖掘、圖像處理和交通控制等領域具有重要的研究意義。國內外學者對近鄰查詢問題進行了廣泛研究，在簡單最近鄰、反向最近鄰、組最近鄰、線段最近鄰和最近對查詢等方面取得了一些重要研究成果［1］。

近年來，由于數據量的顯著增長和實際應用的需要，數據集中的近鄰查詢及其變種問題成為研究的熱點。國內外的研究進一步拓展到移動查詢點的最近鄰查詢［2］、道路網中的連續最近鄰查詢［3-4］、連續集合最近鄰查詢［5］、不確定數據集中的受限最近鄰查詢［6］、可視最近鄰查詢［7］、可視反向最近鄰查詢［8］、高維數據近似最近鄰查詢［9］、不確定數據集的概率頻繁最近鄰查詢［10］、基于Voronoi 圖的反向最近鄰查詢［11］等方面。所取得的成果解決了最近鄰查詢領域的一系列重要問題。

作為最近鄰查詢領域的一個變種問題，單純型連續近鄰鏈(Simple Continues Near Neighbor Chain，SCNNC)查詢在空間數據挖掘、數據相似性分析和智能推理等領域具有較大的作用。已有的研究成果［2-11］無法有效地查詢單純型連續近鄰鏈，為處理單純型連續近鄰鏈問題，文獻［12］基于計算幾何中的Voronoi 圖對數據集中單純型連續近鄰鏈問題進行了研究，提出了一種查詢數據集中單純型連續近鄰鏈的方法。文獻［13］基于空間索引結構R 樹給出了動態數據集中的單純型連續近鄰鏈查詢的算法:SCNNC_R_ST 算法，SCNNC_R_SD 算法和SCNNC_R_XZ 算法。為處理預定數據鏈規模的單純型連續近鄰鏈問題，文獻［14］基于空間Hilbert 曲線給出了查詢算法和更新算法。但文獻［12-14］的研究成果主要適用于無障礙環境下的單純型連續近鄰鏈查詢，不適合處理存在空間障礙物情況下的近鄰鏈查詢問題。由于在現實中空間障礙物的存在較為常見，并且空間數據集往往不是恒定不變的，隨時間和應用的變化，空間數據集經常動態地增加或減少。因此研究障礙物環境下的動態數據集的單純型連續近鄰鏈的查詢具有一定的實際意義。針對已有方法的不足，本文對障礙物環境下的動態數據集的單純型連續近鄰鏈的查詢方法進行研究。

2 基本定義

為了研究障礙物環境下的動態數據集合中的單純型連續近鄰鏈查詢方法，本節首先給出文中所需的基本定義。

定義1 最近鄰查詢［1］

假設有一d 維空間的點集W 和一個查詢點q，最近鄰查詢就是找出子集NN(q，W):NN(q，W)={w∈W|?v∈W:D(q，w)≤D(q，v)}。若要找出w 個最近鄰，該定義則可擴展成w 個最近鄰的查詢，即:wNN(q，W)={v1，v2，…，vw}，其中，?v∈W -wNN(q，W)，w∈wNN(q，W)且D(q，w)≤D(q，v);D(vi，q)≤D(vj，q)，1≤i ＜j≤w。

在定義1 中，D(q，w)和D(q，v)等表示2 個數據點之間的距離。在不強調數據集的情況下，NN(q，W)也可簡寫為NN(q)，表示q 的最近鄰。

基于定義1，下面給出單純型連續近鄰鏈查詢的形式化定義。

定義2 單純型連續近鄰鏈查詢［12］

設有一d 維空間中的數據點集V，V 中一組有序數據點的集合記為CL，CL={vm，vm+1，vm+2，…，vn-1，vn}。其中，vi+1∈NN(vi)(或vi+1?NN(vi)且vi+1∈wNN(vi))，i=m，m+1，…，n-1，稱CL 為V 集中的一條連續近鄰鏈，vm稱為鏈首點，vn稱為鏈尾點。若CL 滿足以下條件，則稱CL 為單純型連續近鄰鏈:

(1)?vi，vj∈CL，若i≠j，則有vi≠vj;

(2)?vi，vj∈CL，若vi+1≠vj+1，則有vi≠vj;

(3)?vi∈CL，vi+1?{vm，…，vi};

(4)?vi∈CL，若vi+1?NN(vi)且vi+1∈wNN(vi)，則有(w-1)NN(vi)?{vm，…，vi}。

在數據集V 中查找一條單純型連續近鄰鏈的查詢稱為單純型連續近鄰鏈查詢，簡記為SCNNCquery。

如圖1 所示，{v1，v2，v3，v4，v5，v6，v7，v8，v9，v10，v11，v12，v13，v14，v15}即是1 條以v1為鏈首點，v15為鏈尾點，共包含15 個數據點的單純型連續近鄰鏈。

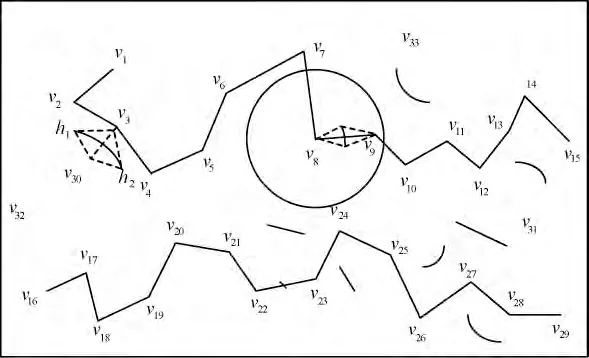
圖1 單純型連續近鄰鏈和空間障礙線

定義3 前驅點/后繼點

在單純型連續近鄰鏈CL 中，設前后有序的相鄰2 個數據點為vi和vj，則稱vi是vj的鏈內直接前驅點，vj是vi的鏈內直接后繼點。本文用PRE(vj)表示vj的鏈內直接前驅點，ACE(vj)表示vj的鏈內直接后繼點。對于CL 中的一個數據點vi，本文稱在CL中排序在vi之前的數據點集為vi的鏈內前驅點集，記為QU(vt)，在CL 中排序在vi之后的數據點集為vi的鏈內后繼點集，記為HJ(vt)。

例如，在圖1 中，v12的鏈內直接前驅點為v11，鏈內直接后繼點為v13，HJ(v11)則為{v12，v13，v14，v15}。

定義4 障礙線

本文中，空間內的障礙物被抽象為直線段或曲線段，統稱為障礙線，記為TLl(如圖1 所示);障礙線的端點稱為障礙邊緣點，記為h。一條障礙線具有2 個障礙邊緣點(如圖1 中的h1和h2所示)。對于數據點對(v，w)，設lVw是v，w 間的直線段，若存在TLl，使得lVw∩TLl≠?且lVw∩TLl?h，則稱數據點v和w 被TLl阻斷，表示為OB(TLl，(v，w));否則，稱數據點v 和w 未被TLl阻斷，表示為┐OB(TLl，(v，w))。

定義5 最短繞障折線

若OB(TLl，(v，w))，稱數據點v 和w 之間的最短距離為最短繞障距離，記為MIN_BL(v，w)，v 和w之間的最短繞障距離連線稱為最短繞障折線，記為lm，lm∩TLl∈h。如圖1 中的折線段v3h2v30。若數據點對(v，w)的繞障折線僅和一條障礙線相關，則稱(v，w)被單級阻斷。

在本文中，如無特殊說明，v 和其無障環境下的最近鄰(NN(v))在有障環境下若被障礙線阻斷，則v和NN(v)被單級阻斷。

定義6 最近鄰判定圓域

設v 和w 之間的最短距離為MIN(v，w)，則以v為圓心，MIN(v，w)為半徑生成的圓域稱為v 的判定圓域。記為Circle(v，MIN(v，w))。若w 是v 的最近鄰，則稱該圓域為v 的最近鄰判定圓域，記為Circle(v，NN_MIN(v，w))。

如圖1 所示，Circle(v8，NN_MIN(v8，v9))即為v8的最近鄰判定圓域。

3 障礙物環境下動態單純型SCNNC 查詢

在現實中，空間數據集往往不是靜態不變的，而是經常會發生動態變化。本文中，障礙物環境下的動態數據集的動態變化主要分為2 類。第1 類是數據集動態增大;第2 類是數據集動態減少。顯然，單純型連續近鄰鏈查詢結果往往會隨著數據集的變化而動態改變。本文3.1 節給出了數據集增大情況下的單純型連續近鄰鏈查詢方法;3.2 節給出了數據集減小情況下的單純型連續近鄰鏈查詢方法。

3.1 數據集增大情況下的單純型連續近鄰鏈查詢

由于障礙物環境下的動態數據集中的單純型連續近鄰鏈的查詢是由數據集的某個初始狀態開始的。本節首先討論障礙物環境下的初始靜態數據集中的單純型連續近鄰鏈的一種啟發式查詢方法(稱為OB_STASCNNC_Search 算法)，其主要思想為:由鏈首點pm 開始調用基于空間索引結構(如空間填充曲線、四叉樹等)的最近鄰查詢算法進行計算，若查詢點與其最近鄰之間無障阻斷，則繼續遞歸進行;如果被阻斷，則進行最近鄰的二次判斷計算，更新部分結果集，遞歸進行，直到查詢出符合要求的近鄰鏈。其中，最近鄰的二次判斷計算可利用障礙判定圓進行。OB_STASCNNC_Search 算法在無障礙物環境下基于空間索引結構進行單個數據點的最近鄰查詢的時間復雜度為O(logn)，計算含w 個連續近鄰鏈點的最近鄰的復雜度為O(wlogn)，設受障礙物影響的鏈中近鄰點對的個數為m，進行最近鄰二次判定的平均計算量為s，則該算法總時間復雜度為O(wlogn+ms)。

當空間數據點動態增加時，障礙物環境下，由鏈首點vm開始的單純型連續近鄰鏈的查詢變得更為復雜。處理該問題的一個較直接的方法(稱為OB_ZJB_UPDATE 方法)即是數據集每次動態更新時，均調用障礙物環境下的靜態數據集的單純型連續近鄰鏈查詢算法(如OB_STASCNNC_Search 算法)進行重新計算。該方法操作較為簡單，但忽略了新增點vnew對查詢的影響細節，對數據集沒有進行預先的過濾判斷，往往會增加許多冗余計算，在數據量較大時，計算代價較大。為了彌補該方法的不足，本小節著重考慮新增點對初始近鄰鏈的影響情況，對數據集進行有效篩選和過濾，提出了新的算法。

針對新增點vnew，為了利用判定圓域對空間數據集進行篩選和過濾，本節首先給出首位點的概念。

定義7 首位點

以一條單純型連續近鄰鏈CL 中的各個點(鏈尾點除外)為圓心，以其到鏈路內直接后繼點的最短距離為半徑所生成的圓域集稱為鏈內最近鄰判定圓域集。圓域集中的一些圓域互相交疊。本文將新增點vnew所位于的鏈內最近鄰判定圓域所對應的圓心點中在鏈內相對位置最靠前(即鏈內序號最小)的數據點稱為vnew相對于判定圓域的首位點。

依據單純型連續近鄰鏈和判定圓的定義與性質可知，在初始單純型連續近鄰鏈CL 生成的情況下，新增點vnew對CL 的影響情況的分析如下:

(1)若新增點vnew落在CL 鏈內最近鄰判定圓域集之外，則對CL 不產生影響。

(2)若新增點vnew落在CL 的鏈內最近鄰判定圓域集之內，則分2 種情況進一步判斷vnew和其在CL中的首位點vt的關系:

1)若vnew和vt之間沒有被障礙物阻斷，則vnew成為vt新的鏈內直接后繼點;

2)若vnew和vt之間被障礙物阻斷，則計算vnew和vt之間的最短繞障距離MIN_BL(vt，vnew)，并和vt及其在CL 中的鏈內直接后繼點ACE(vt)的距離D(vt，ACE(vt))相比較，若MIN_ BL(vt，vnew)大于D(vt，ACE(vt))，則vnew對CL 不產生影響;若MIN_ BL(vt，vnew)小于D(vt，ACE(vt))，則vnew成為vt新的鏈內直接后繼點。若MIN_ BL(vt，vnew)等于D(vt，ACE(vt))，則根據實際需求確定vt的鏈內直接后繼點是否更新。

由以上討論，可得出障礙物環境下數據集動態增大情況下的單純型連續近鄰鏈查詢算法如算法1所示。

算法1 OB_DYNSCNNC_ADD(V，vm，BL，w，vnew)

輸入 空間數據點集V，數據起始點vm，障礙線集BL，待查鏈的數據點數目w，新增數據點vnew

輸出 由鏈首點vm開始的包含w 個數據對象點的一條更新后的單純型連續近鄰鏈CL

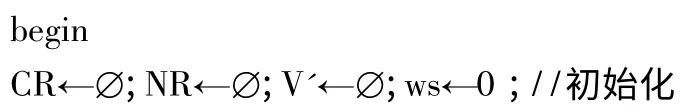
* 判斷新增點vnew和CL 中的數據點的最近鄰判定圓域的位置關系;

//確定vnew所在的數據點的最近鄰判定圓域集NR

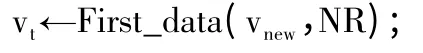
//確定vnew相對于NR 的首位點vt

//更新單純型連續近鄰鏈CL

//更新單純型連續近鄰鏈CL

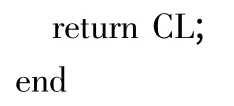
由算法1 的核心步驟可知，該算法初始時調用OB_ STASCNNC_Search 算法生成初始單純型連續近鄰鏈的時間復雜度為O(wlogn +ms)。根據新增點vnew的空間位置，利用鏈內最近鄰判定圓域確定受影響的鏈內點vs的平均時間復雜度為O(s')，由vs為鏈首點開始調用OB_STASCNNC_Search 算法生成部分近鄰鏈的時間復雜度為O(w'logn +m's')，其中，w'是vs之后需要確定的鏈內數據點的個數;m'是需要二次計算和判斷的數據點的個數。該算法核心步驟總的時間復雜度即為O(w+w')logn+ms+m's')。該算法的效率和空間障礙物的數量、空間數據點的數量和受新增點vnew影響的鏈內點的位置關系較大。

3.2 數據集減小情況下的單純型連續近鄰鏈查詢

數據集的動態變化的另一種情況是數據集的動態減小。與3.1 節的討論類似，處理該類問題也可用較為直接的方法(OB_ZJB_UPDATE 方法)。OB_ZJB_UPDATE 方法的主要思想是在數據集每次動態減少時，均調用障礙物環境下的靜態數據集的單純型連續近鄰鏈查詢算法進行重新計算。由于有大量的冗余計算，該方法的計算代價較高。本小節考慮減少點對初始近鄰鏈的影響情況，對數據集進行有效篩選和過濾，提出新的算法。

依據單純型連續近鄰鏈和判定圓的定義與性質可知，在初始單純型連續近鄰鏈CL 生成的情況下，減少點vdel對CL 的影響情況的分析如下:

2015年在2013年所采集的產生抗藥性種群13JLGY-6、13JLGY-9、13JYJD-1、13JCWJ-3的原采集地采集看麥娘種子，分別命名為15JLGY-6、15JLGY-9、15JYJD-1、15JCWJ-3，采用整株生物測定法測定其抗藥性。結果發現，這4個種群看麥娘對精唑禾草靈的相對抗性倍數在9.36～31.79倍之間(表5)。

(1)若減少點vdel不是CL 中的數據點，則CL 不受影響;

(2)若減少點vdel是CL 中的數據點，則減少vdel僅對vdel的鏈內后繼點集有影響，對vdel的鏈內前驅點集沒有影響。只需考慮vdel的鏈內后繼點集的變化更新。

由以上討論，可得出障礙物環境下數據集動態減少情況下的單純型連續近鄰鏈查詢算法如算法2所示。

算法2 OB_DYNSCNNC_DET(V，vm，w，TL，vdel)

輸入 空間數據點集V;數據起始點vm;待查鏈的數據點數目w;障礙線集TL;減少的數據點vdel

輸出 由鏈首點vm開始的包含w 個數據對象點的一條更新后的單純型連續近鄰鏈CL

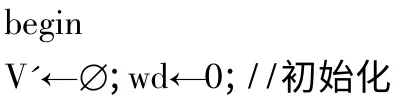
判斷滿足輸入條件的初始單純型連續近鄰鏈CL 是否已生成;

由算法2 的核心步驟可知，該算法初始時調用OB_STASCNNC_Search 算法生成初始單純型連續近鄰鏈的時間復雜度為O(wlogn+ms)。根據刪減點vdel與CL 的關系確定受影響的vdel的鏈內后繼點集的平均時間復雜度為O(s')，由vdel的鏈內直接前驅點vq開始調用OB_STASCNNC_Search 算法生成部分近鄰鏈的時間復雜度為O(hlogn +ts);該算法總的時間復雜度為O((w+h)logn +(m+t)s)，其中，h 是vq之后需要確定的鏈內數據點的個數;t 是vq之后需要考慮的被障礙物阻斷的點對個數。該算法的效率與空間障礙物的數量、空間數據點的數量、數據鏈CL 中受vdel影響的數據點的數量之間的關系較大。

4 實驗結果與分析

本文第3 節研究了障礙物環境下的動態數據集的單純型連續近鄰鏈查詢方法。分別提出了OB_DYNSCNNC_ADD 算法和OB_DYNSCNNC_DET 算法。本節在Pentium4，3.2 GHz CPU、8 GB 內存，Windows XP 環境下，利用C++builder 6.0 對所提出的算法進行實驗分析。實驗數據是在二維空間中利用筆者開發的空間數據生成軟件GEDATA4.0 隨機生成的模擬數據。

設數據集包含的數據量為n，障礙線的個數為g，待查詢的單純型連續近鄰鏈所包含的數據點的數目為w。ζ 表示在不同條件下OB_DYNSCNNC_ADD算法和OB_DYNSCNNC_DET 算法相對于反復調用障礙物環境下的靜態數據集的單純型連續近鄰鏈查詢算法進行計算的直接方法(即OB_ZJB_UPDATE方法)的計算效率的比率。圖2 主要展示了以下3種情況的實驗結果:

情況1 OB_DYNSCNNC_ADD 算法相對于OB_ZJB_UPDATE 方法的計算效率的比較。條件為n 不同，g 和w 相同;(圖2(a)中，g=177，w=225，縱坐標ζ 表示OB_DYNSCNNC _ADD 算法相對于OB_ZJB_UPDATE 方法的計算效率的比率;橫坐標表示數據集中包含的數據量，單位為4K，K=1 024)。

情況2 OB_DYNSCNNC _ADD 算法相對于OB_ ZJB_UPDATE 方法的計算效率的比較。條件為w不同，n 和g 相同;(圖2(b)中，n=10K，g=175，縱坐標ζ 表示OB_DYNSCNNC _ADD 算法相對于OB_ZJB_UPDATE 方法的計算效率的比率;橫坐標表示所查詢的單純型連續近鄰鏈所包含的數據點的個數，單位為K/10，K=1 024)。

情況3 OB_DYNSCNNC_DET 算法相對于OB_ZJB_UPDATE 方法的比較。條件為n 不同，g 和w 相同;(圖2(c)中，g=126，w=210，縱坐標ζ 表示OB_DYNSCNNC_DET 算法相對于OB_ZJB_UPDATE 方法的計算效率的比率;橫坐標表示數據集中包含的數據量，單位為3K，K=1 024)。

由圖2(a)可知，當障礙線的個數g，連續近鄰鏈所包含的數據點的數目w 一定時，隨著數據集包含的數據量增多，OB_DYNSCNNC_ADD 算法相對于OB_ZJB_UPDATE 方法的計算效率的比率將明顯增大。圖2(a)中，當n 為12K 時，其計算效率的比率為2.2，當n 增加到60K 時則提高到4.3。由圖2(b)可知，當數據集包含的數據量n，空間障礙線的個數g 一定時，隨著連續近鄰鏈所包含的數據點的數目w的增多，OB_DYNSCNNC_ADD算法的計算效率將明顯優于OB_ZJB_UPDATE 方法。在圖2(b)中，當w 為0.2K 時，其計算效率的比率為2.0，當w 增加到1.6K 時則提高到5.5。由圖2(c)可知，當障礙線的個數g，連續近鄰鏈所包含的數據點的數目w 一定時，隨著數據集包含的數據量n 增多，OOB_DYNSCNNC_DET 算法的計算效率將優于OB_ZJB_UPDATE 方法。在圖2(c)中，當n 為3K時，其計算效率的比率為1.8，當n 增加到57K 時則提高到4.0。

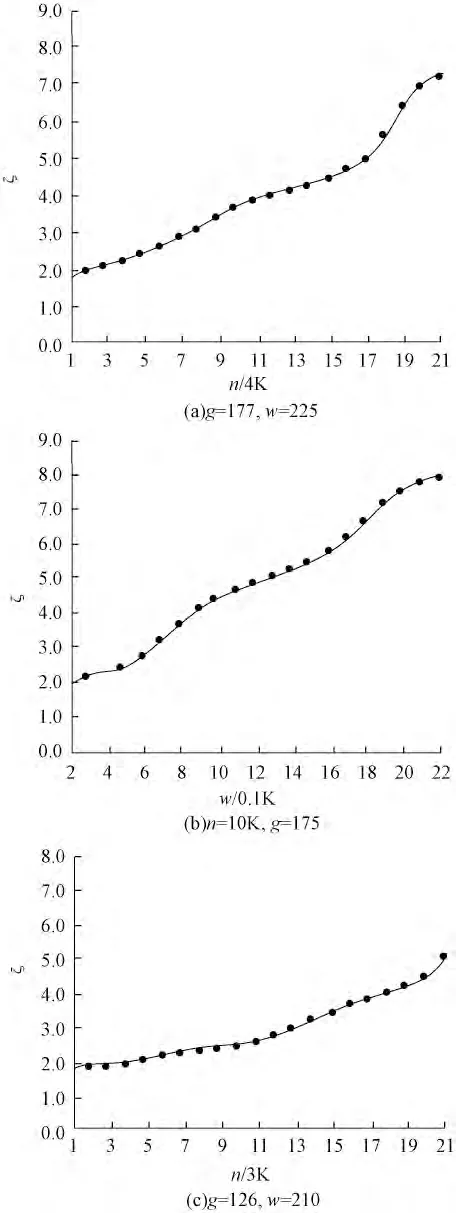
圖2 實驗結果比較

由圖2 的實驗比較可知，在數據集的數據量，待查鏈包含數據點的個數和障礙線的個數較多時，本文提出的算法的優勢更為明顯。在查詢過程中，算法對大量的冗余的數據點進行了預先判斷和過濾，減少了不必要的冗余計算，從而較大程度地提高了查詢效率。

5 結束語

為了處理障礙物環境下的動態數據集中的單純型連續近鄰鏈查詢問題，本文對數據集動態增大和數據集動態減小2 種情況下的障礙物環境下的單純型連續近鄰鏈查詢問題進行研究，分別提出了OB_DYNSCNNC_ADD 算法和OB_DYNSCNNC_DET 算法，并分3 種情況對所提算法進行了實驗比較和分析。理論研究與實驗表明，當數據集的數據量、待查鏈包含數據點的個數和障礙線的個數較多時，本文提出的算法的優勢較為明顯。未來的研究工作主要集中在以下兩方面:(1)將本文的方法和區域關系(如Vague 區域關系［15］)結合處理受限區域中的復雜單純型連續近鄰鏈查詢問題。(2)障礙物環境下的不確定單純型連續近鄰鏈查詢問題。

［1］郝忠孝.時空數據庫查詢與推理［M］.北京:科學出版社，2010.

［2］Song Zhexuan，Roussopoulos N.K Nearest Neighbor Search for Moving Query Point［C］//Proc.of the 7th International Symposium on Advances in Spatial and Temporal Databases.Berlin，Germany:Springer-Verlag，2001:79-96.

［3］Mouratidis K，Yiu M L，Papadias D.Continuous Nearest Neighbor Monitoring in Road Networks［C］//Proc.of VLDB.Seoul，Korea:［s.n.］，2006.

［4］Hu Ling，Jing Yinan，Ku W S，et al.Enforcing k Nearest Neighbor Query Integrity on Road Networks［C］//Proc.of the 20th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.Redondo Beach，USA:ACM Press:346-349.

［5］Elmongui H G，Mokbel M F，Aref W G.Continuous Aggregate Nearest Neighbor Queries［J］.Geo Informatica，2013，17(1):63-95.

［6］Cheng R，Chen J，Mokbel M F.Probabilistic Verifiers:Evalutaing Constrained Nearest-neighbor Queries over Uncertain Data［C］//Proc.of International Conference on Data Engineering.Chicago，USA:［s.n.］:2008:973-982.

［7］Nutanong S，Tanin E，Zhang Rui.Incremental Evaluation of Visible Nearest Neighbor Queries ［J］.IEEE Transactions on Knowledge Engineering，2010，22(7):665-681.

［8］Gao Yunjun，Zheng Baihua，Chen Gencai，et al.Visible Reverse k-Nearest Neighbor Query Processing in Spatial Databases［J］.IEEE Transactions on Knowledge and Data Engineering，2009，21(5):1314-1327.

［9］袁培森，沙朝鋒，王曉玲，等.一種基于學習的高維數據c-近似最近鄰查詢算法［J］.軟件學報，2012，23(8):2018-2031

［10］苗東菁，石勝飛，李建中.一種局部相關不確定數據庫快照集合上的概率頻繁最近鄰算法［J］.計算機研究與發展，2011，48(10):1812-1822.

［11］李 松，郝忠孝.基于Voronoi 圖的反向最近鄰查詢方法研究［J］.哈爾濱工程大學學報，2008，29(3):261-265.

［12］李 松，張麗平，蔡志濤，等.數據集中單純型連續近鄰鏈查詢方法［J］.計算機工程，2012，38(4):82-83，87.

［13］Zhang Liping，Li Song，Li Lin，et al.Simple Continues Near Neighbor Chain Query of the Datasets Based on the R Tree ［J］.Journal of Computational Information Systems，2012，8(22):9159-9160.

［14］張麗平，李 林，李 松，等.預定數據鏈規模的單純型連續近鄰鏈查詢［J］.計算機工程，2012，38(10):51-53.

［15］李 松，郝忠孝.立體空間中的含核Vague 區域系表示與分析［J］.高技術通訊，2011，21(2):157-161.