并行計算中組合空間問題的均衡劃分研究

孫發軍，彭際群

(懷化學院1.數學系;2.高性能并行計算中心，湖南 懷化 418008)

1 組合空間的劃分問題

近年來，隨著云計算的興起，其基礎技術——并行計算更是得到國內外廣泛的研究[1-6].實際應用中通常有這樣一類問題:需要從一個組合空間中通過窮舉搜索尋求最優解或在組合空間上完成一定的計算，如交巡警平臺的增設問題就是這樣一例.

為了更有效地貫徹實施巡警服務職能，需要在市區的一些交通要道和重要部位設置交巡警服務平臺.每個交巡警服務平臺的職能和警力配備基本相同.假設該城市有92個路口，現已經設置20個巡警平臺，根據現有交巡警服務平臺的工作量不均衡和有些地方出警時間過長的實際情況，擬在該區內再增加2-5個平臺，即在72個路口中選擇其中2-5個，使得在平臺個數增加盡可能少的情況下整個城市巡警工作量足夠低且分配平均.

定義1組合空間的劃分問題:并行計算中，給定k個cpu節點，如何把Cnm個組合動態均衡而又連續地分配給各cpu節點去計算的問題.

假設解決該問題的劃分方案需滿足以下要求:

(1)動態性:為了提高速度及滿足一般性需要，我們假設這Cnm個組合是運行時動態生成和分配的.

(2)連續性:為便于各CPU 節點上的并行程序在自己連續的子空間內使用循環完成計算，如窮舉搜索最優解，這就要求劃分組合空間后的子空間應該連續;

(3)均衡性:劃分后所得每一個子空間所含的組合數近似相等，最好能達到完全相等.

為了討論該問題的解決方案是否均衡，我們定義了如下兩個指標[2-4]:均衡指數和加速比.均衡指數用于理論分析中衡量均衡性，而加速比用于通過實驗分析均衡性，因為通常來說均衡性越高所得到的加速比應該越大，而高加速比正是我們讓劃分達到均衡的最終目的.

定義2 均衡指數δ:設分配給n個CPU 節點的任務量分別為q1，q2，…，qn，則我們定義均衡指數為他們之間的標準差:

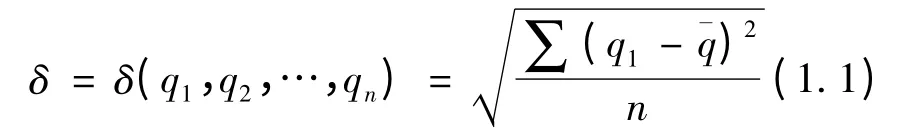
定義3 加速比η:算法串行計算時間ts和算法并行計算時間tp之比，即:

2 均衡劃分研究

以前面描述的交巡警服務平臺增設問題為例，記的組合為(u，v，w，x，y)，(假設已設置的平臺號為0～19，則其中20u87，21v88，22w89，23x90，24y91)，現考慮將該組合空間劃分成16個子空間，以方便將任務分配給16個cpu核并行執行，我們總結出下面的兩類三種方案.

2.1 常規劃分

考慮20u87，計u =20 時的組合為(20，v，w，x，y)，計u =21 時的組合為(21，v，w，x，y)… 計u=87 時的組合為(87，v，w，x，y)，這樣就把C572的組合空間分成了68個u類組合.要將其劃分成16個子空間分配到16個CPU 節點上則可為每個節點分配4-5 (由68 ÷16 =4.25)個u類組合，我們可得到劃分并計算出了每個節點分配到的實際組合數如表1所示(為便于描述，文中所有節點號是CPU 節點號，一般來說一個CPU 節點是一個CPU 核).

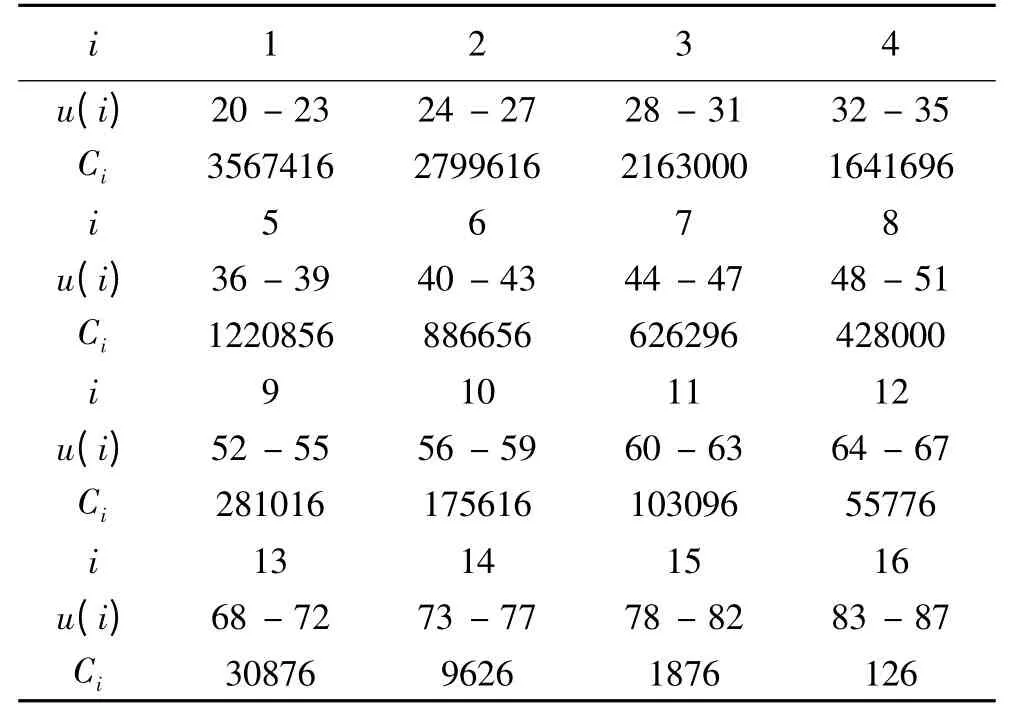
表1 u-均勻劃分方案

記該方案為方案一，其均衡指數為標準差δ1=δ(C1/1000，C2/1000…C16/1000)，計算得到δ1≈1080.5，均衡指數非常大表明各CPU 節點負載非常不均衡，最大值達到3567416個組合.

分析C37的分配情況我們不難發現產生以上現象的原因.C37的組合空間為(1，2，3)，(1，2，4)，(1，2，5)，(1，2，6)，(1，2，7)，(1，3，4)，(1，3，5)，(1，3，6)，(1，3，7)，(1，4，5)，(1，4，6)，(1，4，7)，(1，5，6)，(1，5，7)，(1，6，7)，(2，3，4)，(2，3，5)，(2，3，6)，(2，3，7)，(3，4，5)，(3，4，6)，(3，4，7)，(4，5，6)，(4，5，7)，(4，6，7)，(5，6，7).對于C37的組合(u，v，w)，若以均勻u為依據劃分，很顯然u =1 時的組合數是最多的，u值越大，其組合數越少，當u =5只有一個組合(5，6，7).

2.2 均衡劃分

常規劃分方案雖然實現了并行計算，提高了計算的速度，但因為出現了明顯的負載不均衡現象，沒有充分發掘出任務的并行性.由表1可以總結出，不能以u為標準去劃分整個組合空間，因為對于不同的u，其組合(u，v，w，x，y)的個數本身就是不均衡的.

分析u，v，w，x，y組合的分布規律我們發現，w的組合分布相對更均勻(如表2所示)，表2為不同的k值的組合(u，v，w，x，y)的個數.

于是我們考慮以w(22w89)為標準進行劃分，這樣我們可給每個節點平均分配4-5個w值得到如表3所示的w-均勻劃分方案(記該方案為方案二)，然后可據式(1.1)計算出均衡指數為δ2=462.77，最大值降為1487196個組合，不到常規方案的42%，可見方案二比方案一的均衡性好很多，計算時間理論上可縮小一半以上.

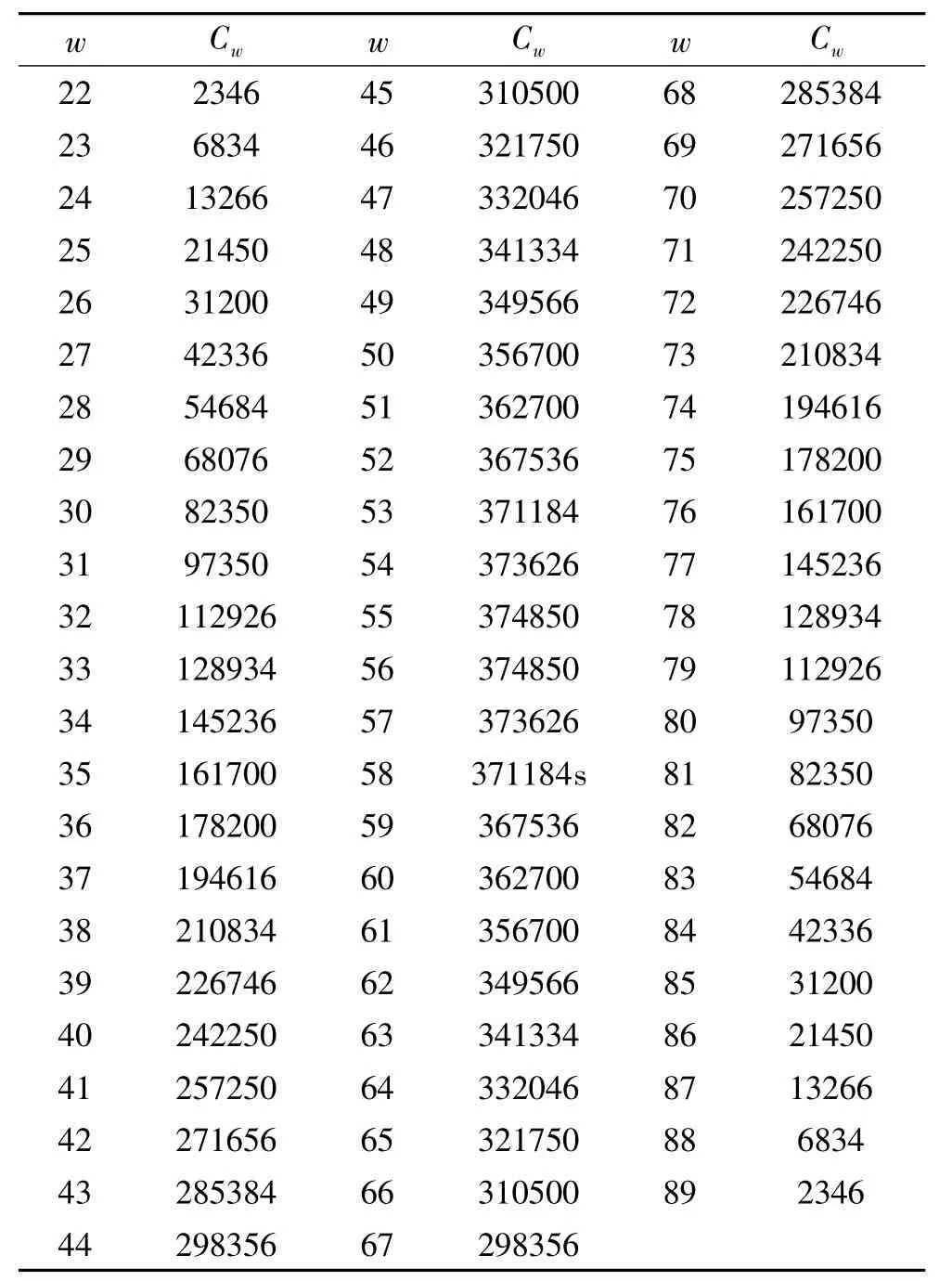
表2 不同w值的組合個數

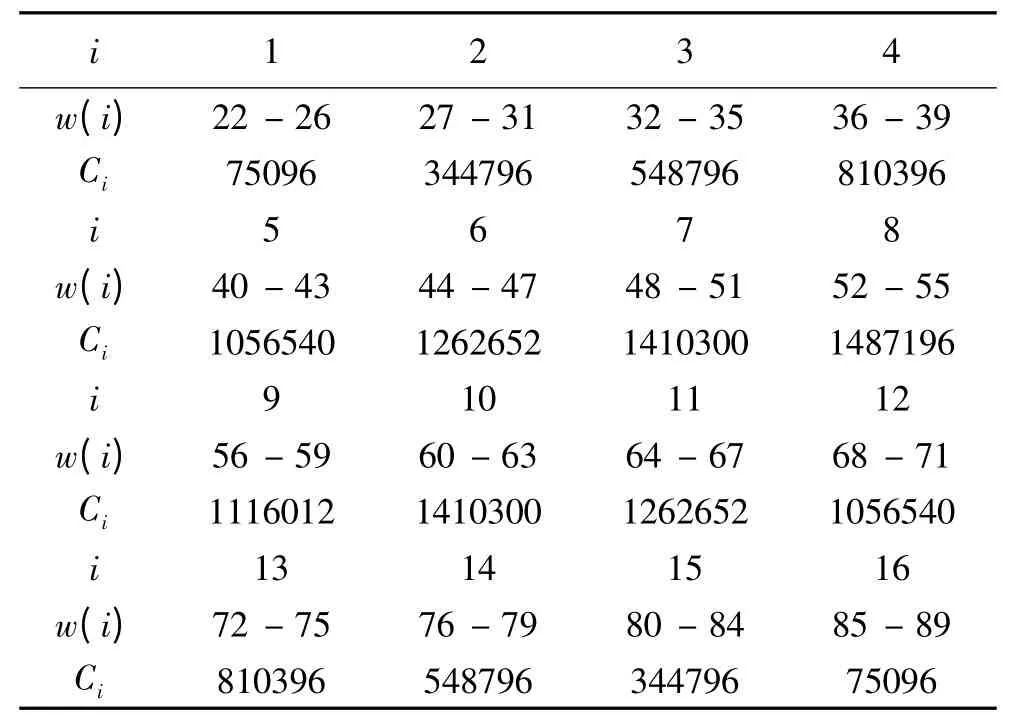
表3 w- 均勻劃分方案

事實上，為使各節點負載更均衡，我們可不均勻分配w值來進行劃分，而是先統計出每一個w的組合(u，v，w，x，y)的個數(如表2所示)，再根據組合個數進行子空間劃分，且對于w=j的組合數與w =111-j的組合數相等.C572=13991544，13991544 ÷16 =874471.5，我們考慮為每個CPU 節點分配800000～900000個組合數，得到如表4所示的分配方案(記為方案三).

由式(1.1)可計算出方案三的均衡指數為，計算δ3=118.24，而最大組合數為1068966，對比方案一下的均衡指數δ1=2.335δ2=9.138δ3，顯然δ3比δ1幾乎小一數量級，從而可知均衡劃分方案下各個CPU 節點負載更為均衡.

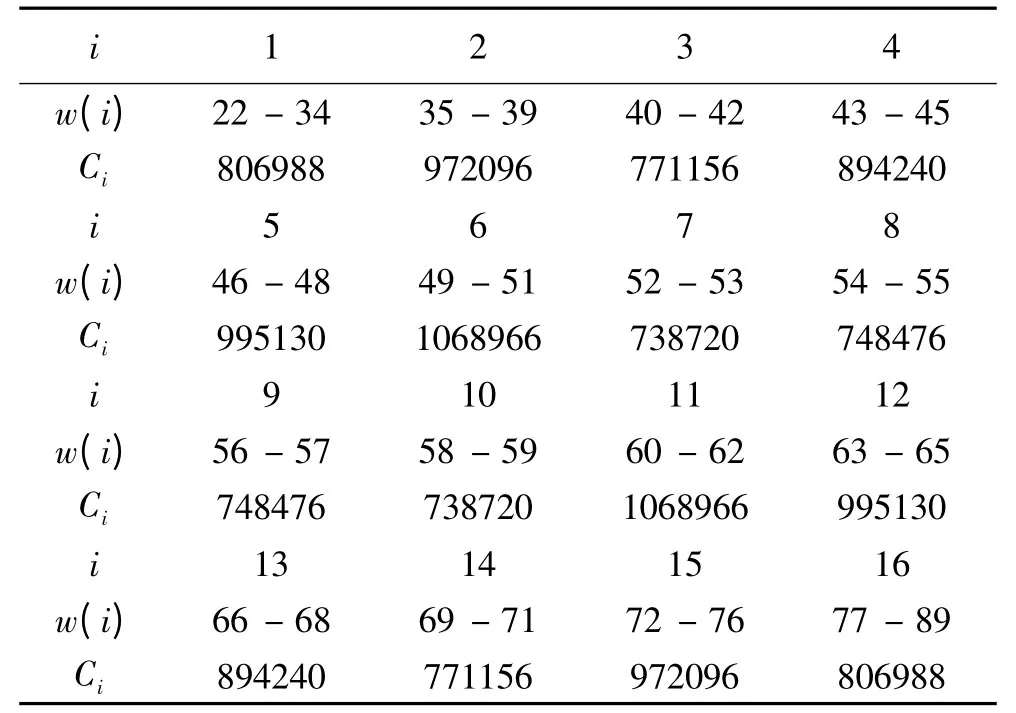
表4 w- 不均勻但更均衡劃分方案

3 均衡劃分的實驗分析

為了便于比較各方案的優劣，我們定義并行計算的加速比為式(1.2)所示.

按這種方案劃分，進行并行計算，發現經過30020.23 s 后計算完畢，速度明顯比單節點串行快(串行所需計算時間為117554.85 s)，我們可據式3.1 計算出其加速比為:

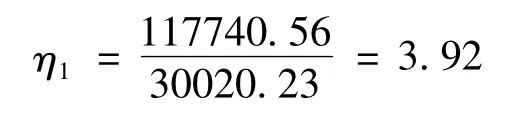
我們在曙光3600 系列服務器集群(10個2 路刀片服務器)上選擇了16個cpu 核對以上三種方案進行了實驗并記錄了相應結果.

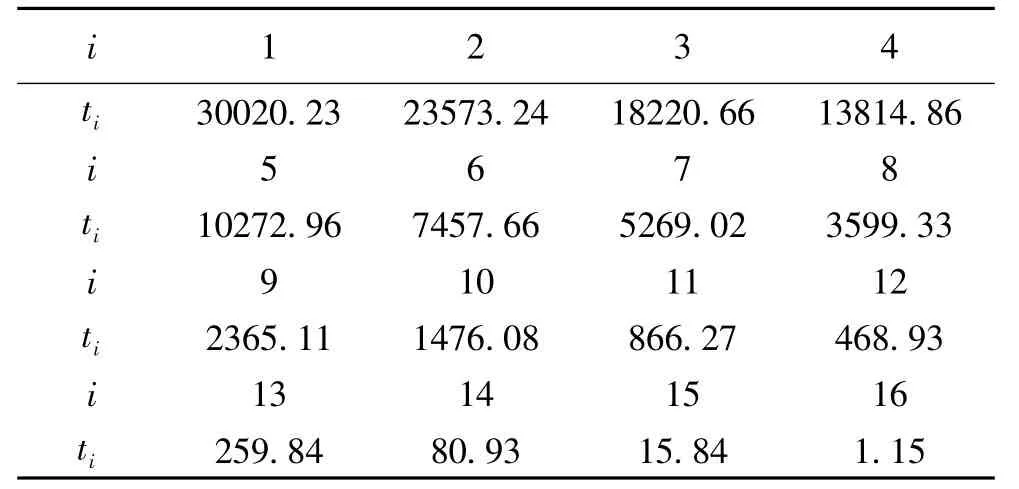
表5 u- 均勻劃分的實驗結果(單位:秒)

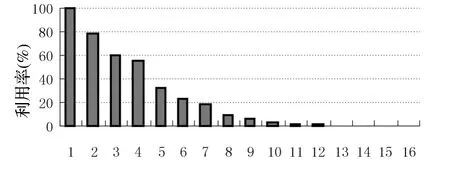
圖1 方案一下16個節點的利用率

實驗中我們記錄的各CPU 上的計算時間如表5所示，記常規方案下第i號CPU 節點的利用率為ei，ei=ti/MAX(t1，…，t16)×100%，得到各個CPU 節點的利用率如圖1所示.從圖1中可以看出，CPU利用率差異很大，該方案下CPU 資源浪費嚴重.

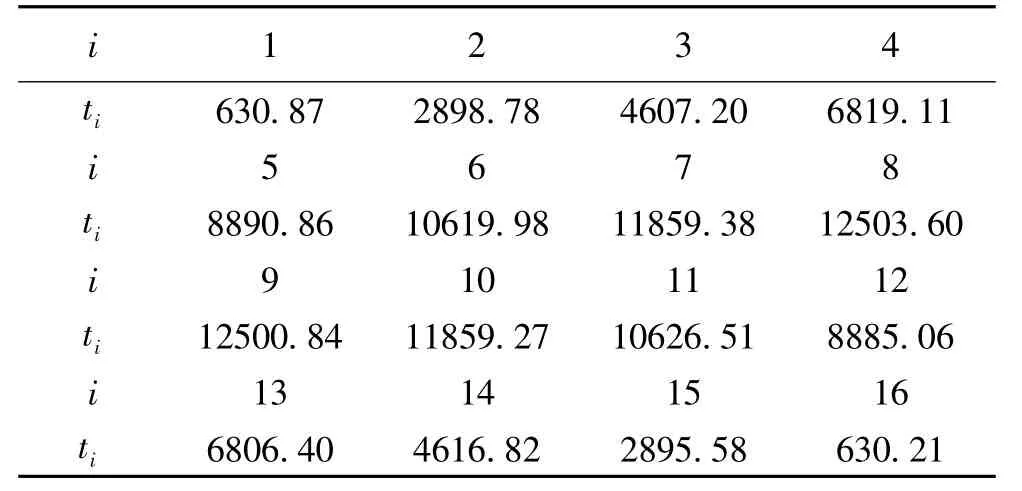
表6 w- 均勻劃分的實驗結果(單位:秒)

我們也記錄了方案二的各CPU 計算時間如表6所示，依式(1.2)我們可計算出加速比為:

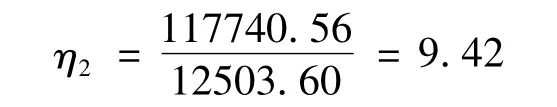
結果表明w-均勻劃分相對于u-均勻劃分提高了2.40倍.

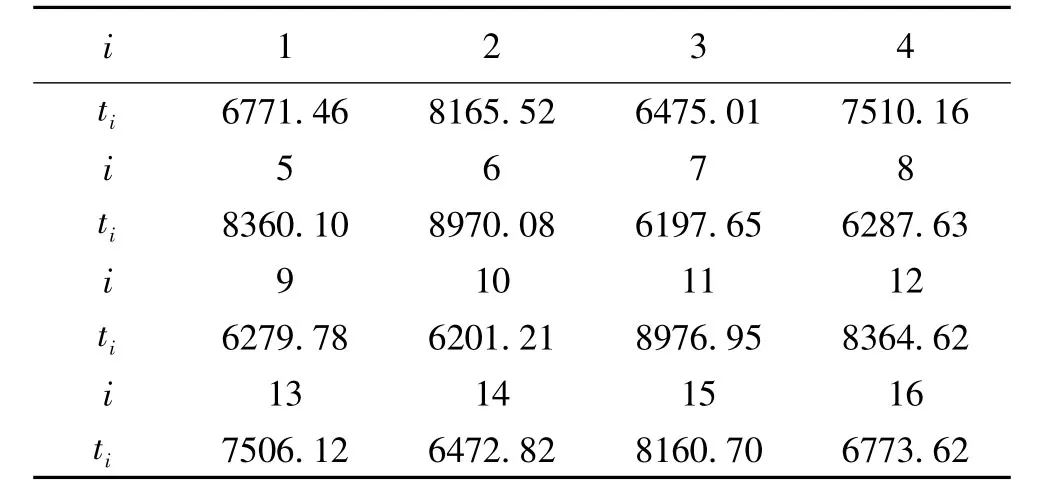
表7 w- 不均勻劃分的實驗結果(單位:秒)

而按方案三進行計算，各CPU的運行時間和利用率分別如表7所示，并可計算出各CPU 節點利用率如圖2所示.

圖2 方案二下16個CPU 節點的利用率

由圖3.4可以看出，16個CPU 節點的利用率均比較高，CPU 資源得到了充分的利用.

同樣我們可計算出加速比為:

該加速比是u-均勻劃分的3.35倍，是w-均勻劃分的1.39倍，與理想值16 僅差2.88.

4 結論

論文提出的組合空間劃分方案充分考慮了CPU負載均衡和各CPU的利用率，進一步挖掘了對稱多處理機上并行計算的效率，但為了方便計算機的執行，組合空間采用了連續分配，導致各個劃分子空間大小仍有差距，在圖2中也可以看出，CPU 利用率最低約為63%，依然存在CPU 資源的浪費，在并行計算過程中會出現一定的負載不均衡現象，探索出方便計算機執行的非連續分配方案，進一步挖掘CPU 資源的利用率，將是后續研究的一個重要內容.事實上若將組合事先均等劃分地存到文件中，然后將文件分派到每個節點上執行.這或許是種效率更高的方案，但從文件中讀數據或許會增大程序的執行時間，從而也降低了計算速度，具體還有待進一步研究.

[1]湯繼飛，李思，張理論，等.面向并行負載平衡的數據剖分技術[J].計算機應用研究，2010，27 (11):4015-4019.

[2]王之元，楊學軍.并行計算系統度量指標綜述[J].計算機工程與科學，2010，32 (10):44-48.

[3]鄭秋亞，劉三陽，左大海，等.多塊結構化網格CFD并行計算和負載平衡研究[J].工程數學學報，2010，27 (2):219-224.

[4]陳國良.并行算法研究方法學[J].計算機學報，2008，31 (9):1494-1502.

[5]馬永剛，譚國真，楊際祥，等.一種改進的并行計算圖劃分模型[J].小型微型計算機系統，2011，32 (3):417-418.

[6]MENON S.Effective reformulations for task allocation in distributed systems with a large number of communicating tasks[J].IEEE Transactions on Knowledge and Data Engineering，2005，14 (12):1497-1508.

[7]Bokhari S H.Assignment problems in parallel and distributed computing[M].Norwell，MA，USA:Kluwer Acadermic Publishers，1987.