三種分類預測模型在醫學中的應用研究

(南方醫科大學 公共衛生與熱帶醫學學院 生物統計學系，廣東 廣州 510515)

在很多醫學診斷和預后研究中都會用到統計預測模型，其中Logistic 回歸是一種常被用于預測結果為二分類變量的統計方法.而神經網絡作為一種新的技術，有學者(如曹志峰)認為它有可能代替Logistic 回歸以及一些別的分類統計方法[1].BP (Back Propagation)神經網絡是目前發展最成熟、應用最廣泛的神經網絡，是一種按誤差逆傳播算法訓練的多層前饋網絡.這一過程可以較迅速地通過調整網絡中的權值以最小化網絡輸出和實際結果的誤差.BP神經網絡首先由Rumelhart，Hinton和Williams 提出，并逐漸在各領域被廣泛應用[2].BP神經網絡在醫學領域中主要應用于疾病輔助診斷，如曹志峰將BP神經網絡運用在甲狀腺疾病的診斷上，結果顯示網絡對樣本的判對率達到99.3%[1].而在BP神經網絡中，由Mackay 提出的貝葉斯正則化的引入[3]，是對傳統BP神經網絡的一種優化模型，可以修正BP神經網絡中常出現的過擬合現象[4]，從而提高其推廣能力[5].國內研究對其應用還不夠廣泛，國外大多學者把這種神經網絡用在工科領域[6-7]，Yu 等人曾將此模型用于卵巢癌的診斷中[8].但總的來說，貝葉斯正則化BP神經網絡在醫學上的應用比較少，遠不及其在工科領域的應用.因此，本文基于一個腎衰竭患者數據，應用BP神經網絡、貝葉斯正則化BP神經網絡與常用的二分類Logistic 回歸對腎衰竭患者是否死亡進行預測，并比較三種模型的預測效果.

1 對象與方法

1.1 數據介紹及其來源

為了比較BP神經網絡、貝葉斯正則化BP神經網絡、Logistic 回歸三者對同一個數據的預測效果，選用了《SPSS13.0 統計軟件應用教程》上的一個關于急性腎衰竭(ARF)的數據[9].該數據為某醫院1990～2000年中所有發生ARF的422名住院患者的臨床資料.該資料共涉及29個變量，其中，器官衰竭和透析方式均為多分類變量，分別有5個水平和4個水平，已被重新分別設置4個啞變量和3個啞變量;計量資料有年齡、血肌酐、血紅蛋白;其它均為二分類變量.把所有多分類變量轉換成啞變量之后，該數據最后共涉及36個變量，見數據文件“ARF.sav”.

實際上，并不是自變量越多得到的模型效果越好，選擇過多的變量往往會增加問題的復雜性，還會影響模型的擬合效果.本研究采用單因素Logistic 回歸對自變量進行篩選，從中選取P值小于0.05的自變量，最終選取了24個自變量:age (年齡)、社會支持、慢性病、手術、糖尿病、腫瘤、cr (血清肌酐)、少尿、lbp(低血壓)、黃疸、昏迷、輔助呼吸、心衰、肝衰、出血，呼衰、器官衰竭2個、器官衰竭3個、器官衰竭4個、dic (彌散性血管內凝血)、敗血癥、感染、透析方式1、透析方式3.

1.2 方法介紹

1.2.1 BP神經網絡

典型的BP神經網絡，是一個含有隱含層(既不屬于輸入層也不屬于輸出層，可同時存在多個隱含層)的三層網絡結構，如圖1所示.

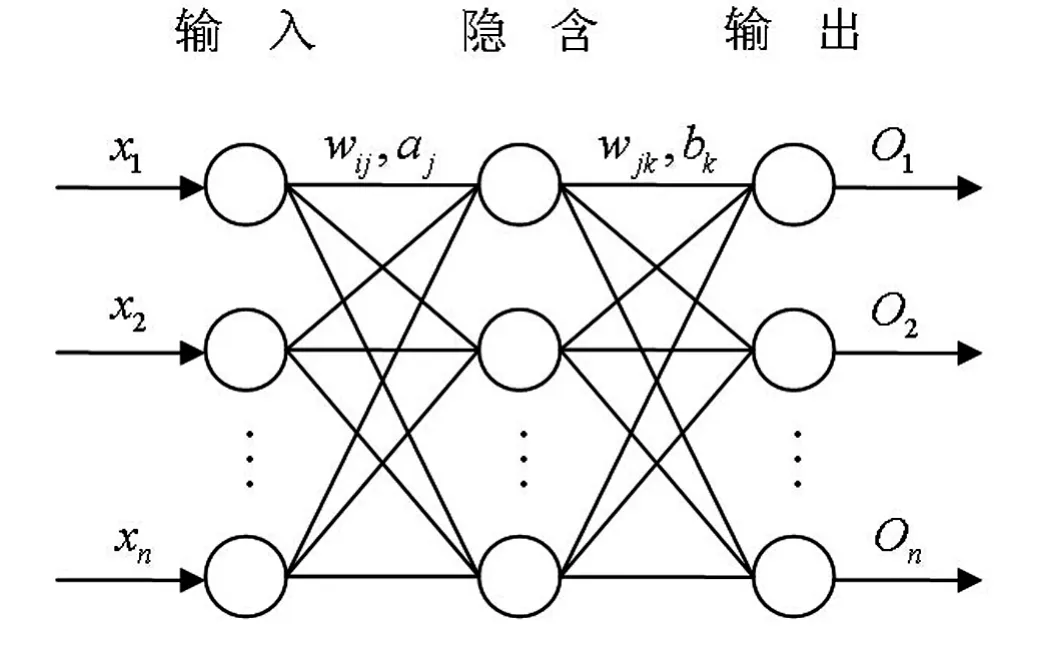
圖1 BP神經網絡基本結構

BP神經網絡訓練主要分兩個過程:輸入變量的前向傳播以及誤差反向傳播.全程流程圖如圖2所示.

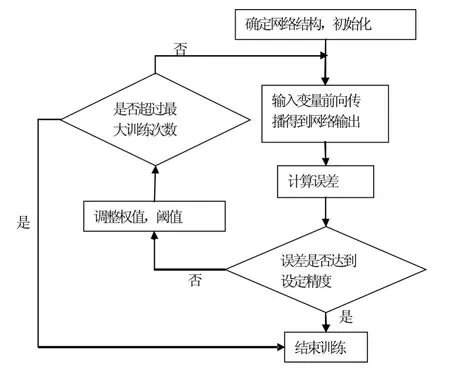
圖2 BP神經網絡訓練流程

具體訓練步驟如下:

(1)確定網絡結構.

①確定隱含層層數.

1989年Robert Hecht-Nielson 已經證明對于任意閉區間內的一個連續函數，都可以用只含有一個隱含層的BP神經網絡來逼近.本研究選用單個隱含層[10].

②確定隱含層節點數[11].

隱含層節點的選取，到目前還沒有完善的理論依據，大多以經驗為主，且有多種可參考原則，本研究用以下原則來確定隱含層節點數:m =log2n，其中，n為輸入層節點數，m為隱含層節點數.本研究計算得出m約為4.55，四舍五入，以5為隱含層節點數.

③確定激活函數類型[12].

理論上已證明，至少一個S 型隱含層加上一個線性輸出層的神經網絡，能夠逼近任何有理函數.因此，本研究隱含層激活函數f選用tansig 函數，輸出層函數g選擇purelin 函數.

(2)初始化[12].

根據樣本輸入、輸出變量確定網絡輸入、輸出層節點數n，其中，輸入、輸出層節點數可以不同，如當輸入節點數為c，輸出節點數為d時，神經網絡就表達了從c個自變量到d個因變量的函數映射關系.初始化輸入、隱含和輸出層間的權值wij和wjk，隱含、輸出層閾值aj和bk，其中i=k =1，2，…，n，j =1，2，…，m.(此處i=k是指輸入層節點與輸出層節點個數一致).學習速率設為0.01 (常用)，最大訓練次數設為20000，目標精度設為0.

(5)誤差反向傳播[2]，根據梯度下降算法更新權值wij和wjk，閾值aj和bk.如:wjk(l+1)= wjk(l)+Δwjk= wjk(l)+ηδkHj、wij(l+1)= wij(l)+Δwij=wij(l)+ηδjxi、bk(l+1(= bk(l)+Δbk=bk(l)+ηδk、aj(l+1)=aj(l)+Δaj=aj(l)+ηδj.其中，η為學習速率，δk為輸出層誤差，δj為隱含層誤差，l =1，2，…，M為訓練次數.

1.2.2 貝葉斯正則化BP神經網絡

實際上，貝葉斯正則化神經網絡是在BP神經網絡誤差反向傳播后增加一個貝葉斯正則化優化參數的過程.因此，對于貝葉斯正則化BP神經網絡中BP神經網絡那一部分的參數設置和計算等不再贅述，而貝葉斯正則化優化參數這一過程又分為正則化和貝葉斯推理兩個部分，步驟如下[3，5，14]:

這里，我們記網絡模型訓練樣本集D =(xi，yi)，i=1，2，…，n，令網絡框架為A(包括網絡層數、每層節點數、激活函數類型)，網絡參數為w(包括三層間所有的權閾值)，網絡模型為O(x;w，A)，誤差函數為ED(D|w，為了縮減網絡復雜度，給誤差函數加一個權罰項1，2，…N.注意，這里提到的i和m在本節中分別表示樣本數和網絡參數(權值閾值)個數，不要與前面提及的記號混淆.由ED和Ew綜合成一個新的目標函數(目標是指整個算法的最優化目標):M =αEw(w | A)+βED(D| w，A).其中，α，β為“黑箱子(black box)”參數[3]，也叫超參數[14].實際應用時，最小化目標函數是為了減少網絡訓練誤差的同時降低網絡結構的復雜度.因為常規的正則化方法一般很難確定正則化參數的大小，而采用貝葉斯理論可以在網絡訓練過程中自適應地調節正則化參數大小并使參數達到最優，最后經過一系列推導，可以得到其中，γ=N-2αtr(M(wMP))-1，wMP表示M取最小值時所對應的網絡參數值;γ表示有效的網絡參數個數，反映網絡的實際規模;N是網絡中所有參數的個數.

1.3 軟件實現及方法

用SPSS 21.0 對原數據中的變量進行篩選，以不同分界點作Logistic 回歸并得出相應的判對率，畫出三個模型的ROC 曲線并計算其AUC;用Matlab 訓練BP神經網絡和貝葉斯正則化BP神經網絡并以不同分界點計算其判對率.

2 結果與討論

2.1 不同分界點下三種模型判對率的比較

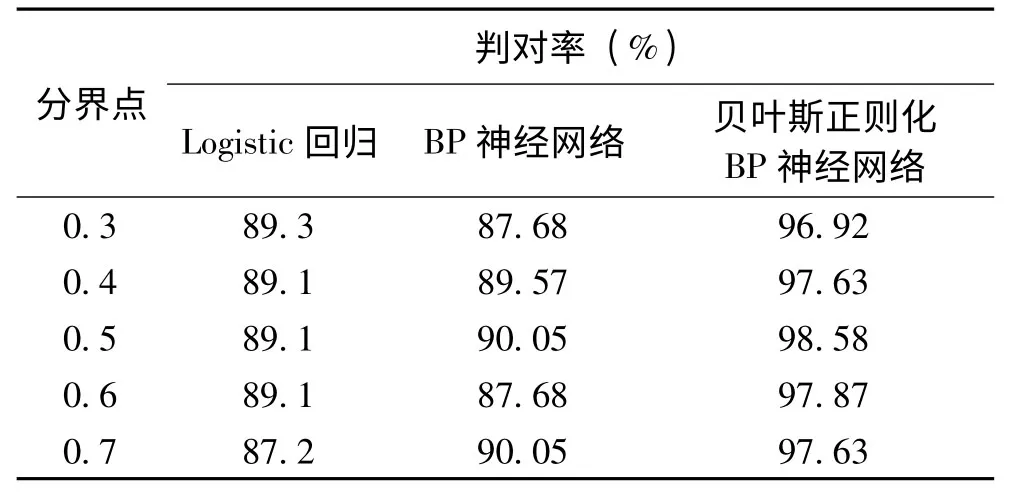
表1 不同分界點下三個模型的判對率

比較不同分界點下三個模型對同一數據的預測效果，觀察分界點的選擇對三個模型預測效果的影響，選擇了0.3、0.4、0.5、0.6 與0.7 五個分界點，結果見表1.可見三個模型以0.5為分界點時判對率最高.此時，Logistic 回歸模型的靈敏度為81.6%，特異度為93.4%;BP神經網絡模型的靈敏度為84.6%，特異度為93.1%;貝葉斯正則化BP神經網絡模型的靈敏度為96.3%，特異度為99.6%.

2.2 三個模型ROC 曲線及曲線下面積(AUC)比較

以三個模型輸出的原始結果為基礎畫出三個模型的ROC 曲線(圖3)并求出曲線下面積(表2).直接比較兩個ROC 曲線下面積的95%可信區間是否交叉，如交叉，則表明兩個ROC 曲線下面積在α =0.05時無顯著差異;如不交叉，則有統計學差異[15].可見，BP神經網絡和Logistic 回歸比較，它們的AUC 無顯著差別，而貝葉斯正則化BP神經網絡和上述二者比較，它們的AUC 有顯著差別，且貝葉斯正則化BP神經網絡AUC為三者中最大者，即模型預測效果最好.

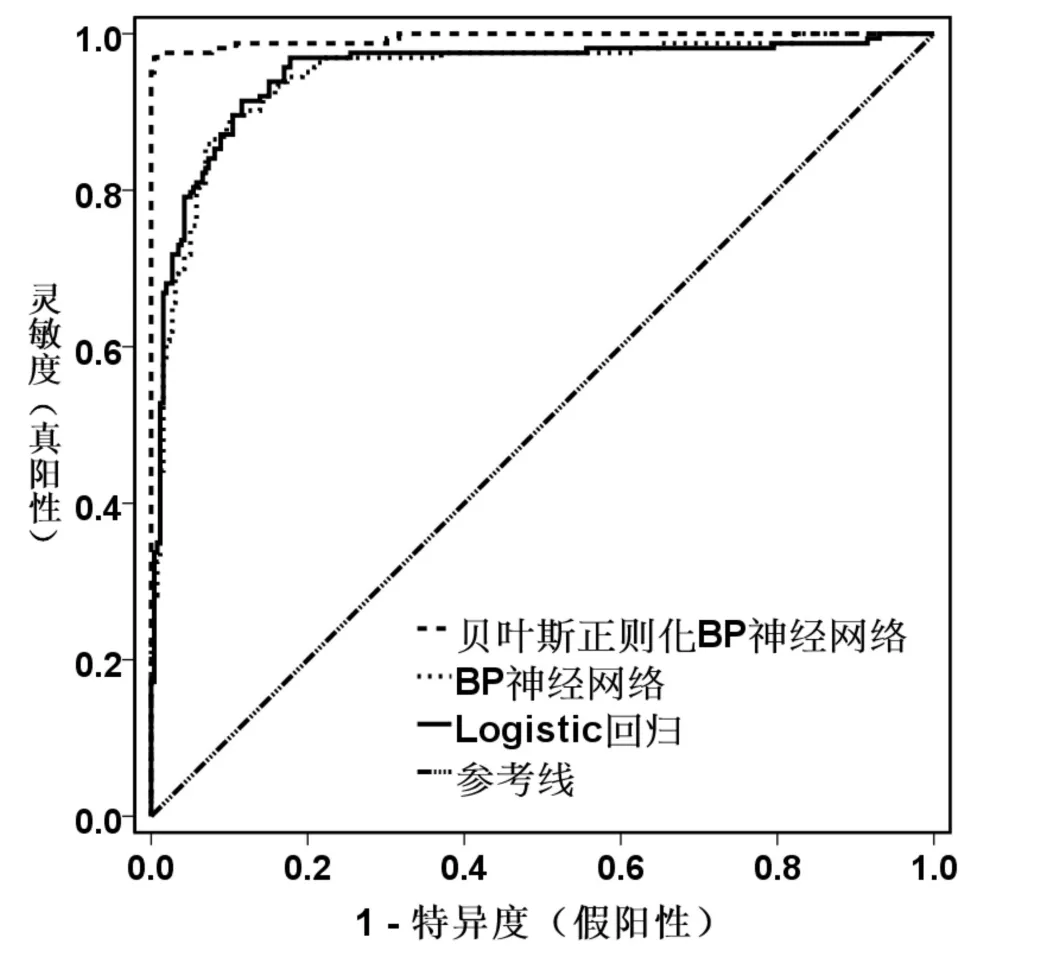
圖3 三個模型ROC 曲線圖

表2 三個模型AUC 及95%置信區間

3 結論

針對本研究的數據，當三個模型的輸出結果都以0.5作為分界點時，它們的判對率分別為89.1%(Logistic 回歸)、90.05% (BP神經網絡)和98.58%(貝葉斯正則化BP神經網絡).用三個模型原始輸出結果和目標數據作比較畫出的ROC 曲線及求得的AUC分別為0.950、0.947和0.995.可見，針對這一數據，BP神經網絡的預測效果并不像大多數以往研究中所說的會比Logistic 回歸結果好[1，16-17]，反而是和Logistic回歸得出的結果差不多，但是貝葉斯正則化BP神經網絡的預測效果比上述兩個模型好很多.當然，不排除是由于數據樣本量不足導致BP神經網絡不能得到很好的訓練，從而預測效果不如理想中準確.不過，本研究突出了貝葉斯正則化BP神經網絡不需要大量的訓練樣本也能得到很好的輸出結果這一優點.

[1]曹志峰.BP神經網絡在臨床診斷中的應用與探討[J].實用醫技雜志，2005，12 (9):2656-2657.

[2]Rumelhart D E，Hinton G E，Williams R J.Learning representations by back-propagating errors[J].Nature，1986，323 (9):533-536.

[3]MacKay D J C.A practical Bayesian framework for backpropagation networks[J].Neural computation，1992，4 (3):448-472.

[4]Moody J，Hanson S J，Lippmann R P.The Effective Number of Parameters:An Analysis of Generalization and Regularization in Nonlinear Learning Systems[J].Advances in neural information processing systems，1992，4:847-854.

[5]魏東，張明廉，蔣志堅，等.基于貝葉斯方法的神經網絡非線性模型辨識[J].計算工程與應用，2005，41(11):5-8.

[6]Auld T，Moore A W，Gull S F.Bayesian neural networks for internet traffic classification[J].Neural Networks，IEEE Transactions on，2007，18 (1):223-239.

[7]Goh A T C，Kulhawy F H，Chua C G.Bayesian neural network analysis of undrained side resistance of drilled shafts[J].Journal of Geotechnical and Geoenvironmental Engineering，2005，131 (1):84-93.

[8]Yu J，Chen X W.Bayesian neural network approaches to ovarian cancer identification from high-resolution mass spectrometry data[J].Bioinformatics，2005，21 (1):i487-i494.

[9]陳平雁.SPSS 13.0 統計軟件應用教程[M].北京:人民衛生出版社，2005，196-197.

[10]Hecht-Nielsen R.Theory of the backpropagation neural network[J].International Joint Conference on IEEE，1989:593-605.

[11]MATLAB 中文論壇編著.MATLAB神經網絡30個案例分析[M].北京:北京航空航天大學出版社，2010，9-10.

[12]聞新，周露.MATLAB神經網絡應用設計[M].北京:科學出版社，2000:225-232.

[13]MacKay D J C.Bayesian interpolation[J].Neural computation，1992，4 (3):415-447.

[14]李鵬.基于貝葉斯理論的神經網絡算法研究[J].光機電信息，2011，28 (1):28-32.

[15]DeLong E R，DeLong D M，Clarke-Pearson D L.Comparing the areas under two or more correlated receiver operating characteristic curves:a nonparametric approach[J].Biometrics，1988:837-845.

[16]黃德生，周寶森，劉延齡等.BP人工神經網絡用于肺鱗癌預后預測[J].中國衛生統計，2000，17 (6):337-340.

[17]Peng SY，Peng SK.Predicting adverse outcomes of cardiac surgery with the application of artificial neural networks[J].Anaesthesia，2008，63 (7):705-713.