一種基于帶寬調度的網絡擁塞控制策略
孫洪濤,吳敬,李婭,秦朋
(1.山東外國語職業學院信息工程學院,山東日照276826;2.沈陽志成電子工程有限公司,遼寧沈陽110000)
隨著計算機和通信技術的飛速發展,控制系統的規模越來越龐大,分散化程度越來越高,傳統的點對點控制已經無法滿足復雜工程系統對控制系統結構的要求。通過網絡形成閉環的控制系統稱為網絡控制系統(networked control system,NCS)[1-2]。NCS將閉環控制回路分散于實時網絡上,突破了傳統控制系統在空間物理位置上的限制以及信息的封閉和局限性,已成為現代大規模復雜控制系統的首選構架,是目前國際控制領域的研究熱點。
由于網絡本身的固有特性,網絡的引入也給控制系統分析和綜合帶來很多新問題[3],如網絡帶寬資源的有限性、網絡中信息傳輸的速率與傳輸中的延遲、信息的量化以及分布式的控制方式等。NCS由通訊網絡和控制系統組成,有限的網絡帶寬始終是其瓶頸問題。在分析和設計網絡控制系統時,必須綜合考慮通訊網絡與控制系統的耦合,進行控制與調度協同設計,以期同時保證控制系統品質(quality of performance,QoP)和網絡服務質量(quality of service,QoS)。NCS中控制與調度的協同設計已被越來越多的學者所關注[4],開始人們注重控制算法的設計[5-9],通過將時延、數據包丟失等問題融入到控制器的設計中來保證控制系統的穩定性,提高控制性能,此類控制算法將網絡因素包含在控制器設計上,只是形式上的聯合,并未考慮到網絡的QoS。隨著研究的深入,當網絡中信息傳輸不暢導致原有的控制算法難以施行,反過來又提高了控制器設計的難度時,催生了注重于網絡資源分配的調度策略,通過帶寬分配及采樣周期的調整不僅提高了QoS,而且從側面提高了控制算法執行的有效性,從而達到真正意義上的NCS協同設計[10-14]。綜上所述,較好的網絡服務質量是保證控制系統品質的前提。因此,在保證控制系統QoP的前提下,有必要對NCS中的網絡進行進一步的研究[15-16],在有限的網絡資源下提高其綜合性能。
從通訊網絡角度來看,NCS中的時延、數據丟包等問題歸根結底是因不同控制回路的帶寬受限造成的信息不能及時傳輸或傳輸不暢,進而導致了控制器的數據無法及時更新,降低了控制系統的控制性能。通常,若用網絡擁塞程度來表征數據通道中的傳輸狀態,可以得出控制回路中的網絡擁塞程度與帶寬密切相關。針對因網絡服務質量引起的網絡控制系統綜合性能的下降,本文建立了基于網絡擁塞和帶寬之間的線性時不變模型,通過最優的動態帶寬分配實現對網絡擁塞的實時控制,從而保證網絡處于一個較為穩定的運行狀態,降低QoS對控制系統性能的影響。
1 問題描述
考慮如圖1所示的NCS。在該系統中,各個控制回路在執行控制功能時都需要通過網絡進行信息的采集、運算及傳輸,在通過網絡進行信息采集和傳輸數據時不同回路都需要占用一定的網絡帶寬。帶寬可以用來衡量信息傳輸能力,較大的帶寬能夠在單位時間內傳輸較多的數據量,那么該控制回路的網絡擁塞程度低,網絡狀態較穩定;較小的帶寬在單位時間內只能傳輸較少的數據量,那么該控制回路的信息擁塞程度高,網絡狀態較不穩定。同時,網絡運行狀態可用網絡擁塞程度來表示。在此,定義網絡擁塞程度為狀態xj(j=1,2,…,m),各個控制回路帶寬為bi(i=1,2,…,p)。調度器采集執行器側的信息擁塞狀態xj,對傳感器側的帶寬進行分配,通過合理的帶寬分配來消除網絡擁塞,從而保證網絡運行狀態的穩定。
為建立網絡擁塞狀態xj與網絡帶寬bi的線性時不變模型,首先給出如下定義和假設:
定義1 如果沒有網絡擁塞的發生,則定義為網絡的穩定狀態(零狀態);網絡擁塞程度越大,網絡的狀態越不穩定;同時,網絡沒有發生擁塞時能夠傳輸的最大數據量所占用的帶寬定義為基本帶寬,相應的采樣周期稱為基本采樣周期。
定義2 若在原有穩定網絡狀態下控制系統面臨擾動,需要更多的數據傳輸以達到被控對象的鎮定,相比于基本帶寬所能傳輸的數據量,需要額外傳送的數據量稱為額外數據量。故網絡的擁塞狀態可定義為在基本帶寬情形下需通過網絡傳輸的額外數據量
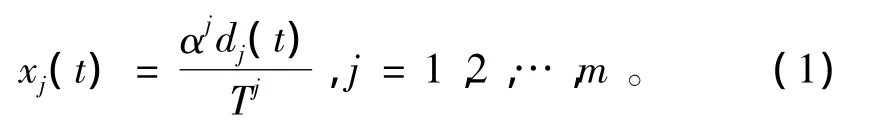
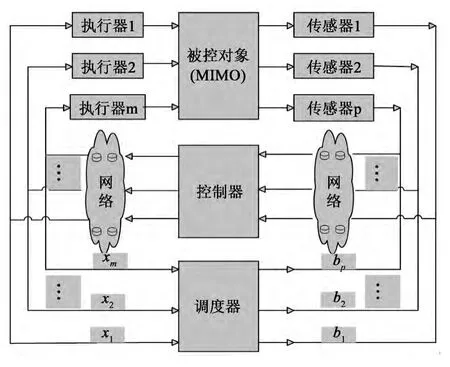
圖1 含有調度器的NCS模型Fig.1 Structure of NCS containing a scheduler
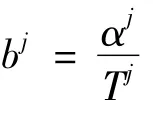
由此可見,在基本采樣周期時間內,通過網絡進行傳輸的額外數據量越大,網絡擁塞就越嚴重,若不進行額外數據傳輸,則xj=0,說明信息擁塞被消除。
假設1 如果沒有網絡擁塞發生,則給出的控制器設計對于控制系統是有效的;并且,控制器的存在不影響網絡的動態行為。
假設2 網絡的擁塞狀態xj和控制回路帶寬bi存在如下線性關系

其中,X(·),B(·)是網絡擁塞狀態函數和控制回路帶寬函數,α1,α2,…,αn為任意有限非零常數。也就是說,網絡擁塞狀態xj與帶寬bi滿足齊次性與可加性。
基于以上定義和假設,給出如下信息擁塞狀態與帶寬之間的LTI模型:

其中,x= [x1,…,xn]T∈Rn表示網絡擁塞狀態向量,u= [u1,…,up]T∈Rp是含有帶寬量的控制變量,A,B是適維矩陣。
本文的主要目的是通過動態的最優帶寬分配來消除網絡中的信息擁塞,從而提高網絡的QoS。
對系統(3),給出如下最優反饋控制器



2 最優化求解方法
由上節分析可知,該問題的最優化求解是一個典型的線性二次型問題[18]。若網絡產生擁塞偏離平衡狀態后,希望以最優的帶寬分配方式消除網絡擁塞以保持網絡運行的穩定狀態。考慮到實際應用,應采用無限時間狀態調節器,以便于實時控制。根據上述LTI模型可定義最優性能函數

其中,Q≥0,R>0為線性二次型權值矩陣且是適維的。
根據(5)式確定最優的帶寬消耗使性能指標J達到最小。因為積分上限tf→∞,J有可能無界,為避免此類情況,故要求系統(3)可控,即秩R(A,B)=m。

引理1 對任意矩陣∑,∑∑T=Q,P是Riccati方程的解,則(A,∑)完全可觀的充分必要條件是P為正定對稱矩陣。
其次,我們以定理1的形式給出該問題的最優解。
定理1 若給定的陣對(A,B)可控,(A,∑)可觀,則存在唯一的最優帶寬控制

且最優性能指標為

其中,各個矩陣的含義同上。
最后,給出了在此最優帶寬分配策略下網絡運行狀態的穩定性證明。
結合式(4)、(7),則最優閉環系統可寫為

其中,x(0)=x0為網絡擁塞的初始狀態。

上式對時間t求導可得

根據式(9),式(11)可進一步寫成



和

將式(4)代入式(14),則

因為R>0,所以u*T(t)=0。也就是說系統(3)只有零輸入響應

將式(16)代入式(13)得

其中,∑∑T=Q。
式(17)表明

這與(A,∑)可觀相矛盾。
證畢。
3 數值仿真
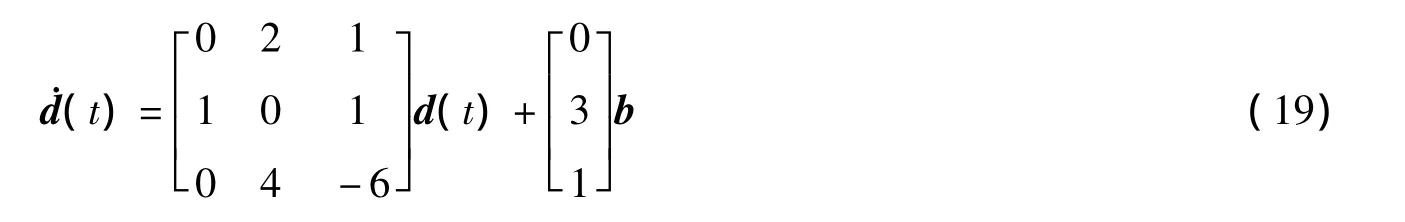
其中,d是額外數據量,b是帶寬。


最后,通過MATLAB仿真給出了網絡擁塞的狀態軌跡曲線,見圖2。
顯然,2.7 s后信息擁塞被消除,求得最優性能指標J=2.057 1。同時,可得出帶寬的實時變化曲線,見圖3。
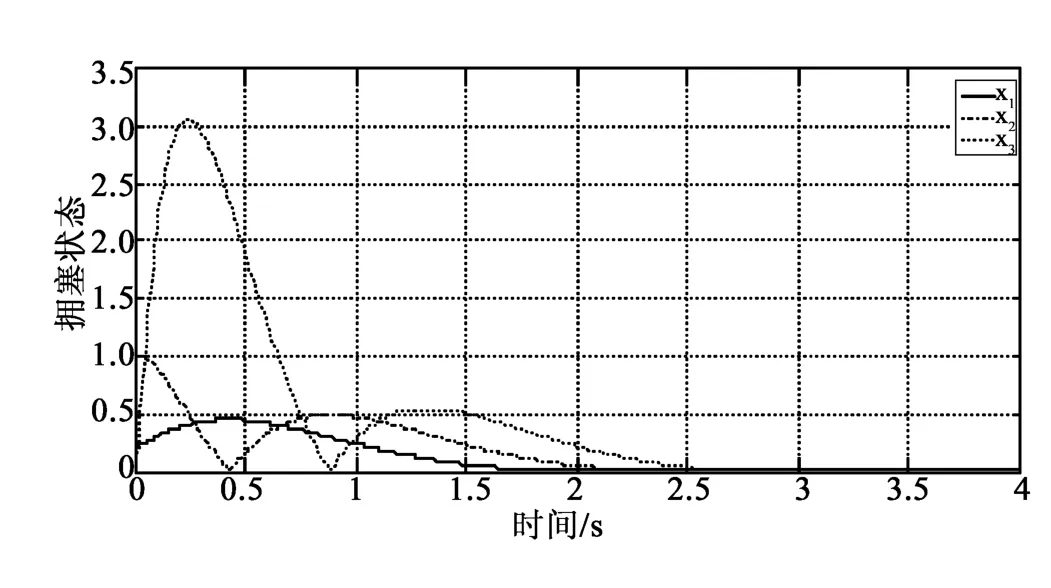
圖2 信息擁塞狀態變化軌跡Fig.2 Variation trajactory of network congestion state
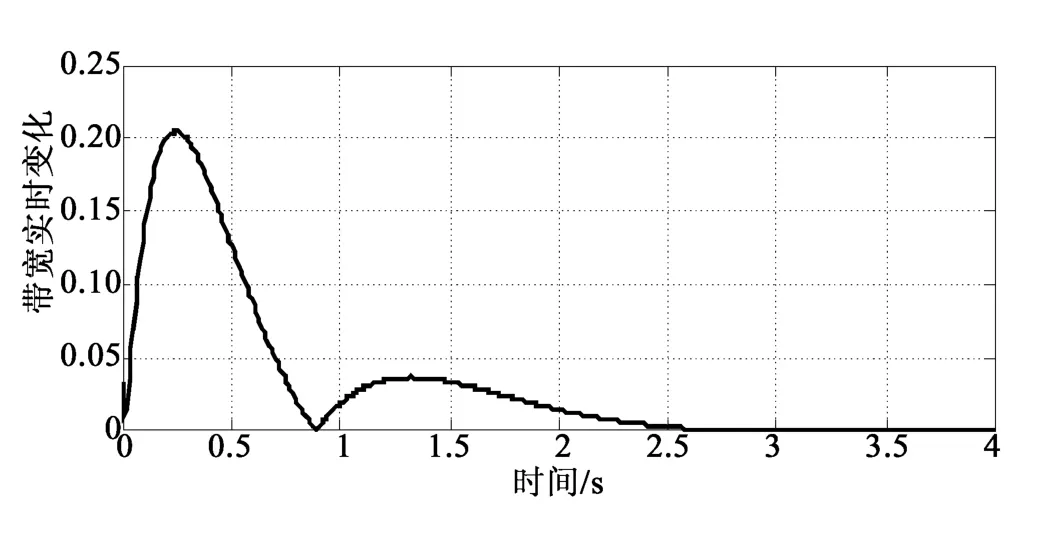
圖3 帶寬實時消耗曲線Fig.3 Bandwidth realtime consumption curve
本文中帶寬被視為一種“能量”用來消除網絡中的信息擁塞,即通過合理調整網絡中帶寬大小,來保證網絡始終運行在一個相對穩定的狀態而沒有網絡擁塞的發生。圖2表明通過本文提出的帶寬控制器設計方法能夠有效消除網絡擁塞,圖3中的曲線則反應了帶寬的實時變化,但并不意味著當網絡擁塞被消除后帶寬也變為零。因為當網絡狀態趨于穩定時,只說明各個閉環回路只是保持原有的未發生網絡擁塞時基本帶寬,不再需要額外的帶寬,即沒有額外的數據需要傳輸時,不需分配額外的帶寬。仿真結果表明,該擁塞控制策略是有效的。
4 結語

[1]WANG Z W,GUO G.Fundamental issues and prospective directions in networked multirate control systems[J/OL].Mathematical Problems in Engineering,2014,http://dx.doi.org/10.1155/2014/513506.
[2]BRINDHA M,MENDIRATTA J K.Networked control system-A survey[J].International Journal of Modern Education and Computer Science,2013,5(6):42-48.
[3]游科友,謝立華.網絡控制系統的最新研究綜述[J].自動化學報,2013,39(2):101-118.
[4]SETO D,LEHOCZKY J P,SHA L,et al.On task schedulability in real-time control systems[C]//17th IEEE Real-Time Systems Symposium,1996.Piscataway:IEEE,1996:13-21.
[5]BATISTA A P,JOTA F G.On the effects of time delay variations in the design of networked control system[J].International Journal of Systems,Control and Communications,2013,5(2):120 -139.
[6]XU S J,CAI X S,GAO H.Output-feedback design of networked control systems and estimating maximum data packets dropout[C]//2013 25th Chinese Control and Decision Conference(CCDC).Piscataway:IEEE,2013:3109-3113.
[7]TORRES G,VELASCO M,MARTI P,et al.An alternative discrete-time model for networked control systems with time delay less than the sampling period[C]//39th Annual Conference of the IEEE Industrial Electronics Society,IECON 2013.Piscataway:IEEE,2013:5626-5631.
[8]GUO X L.Controller design based on variable period sampling approach for networked control systems with random delays[C]//International Conference on Networking,Sensing and Contro1,2009.Piscataway:IEEE,2009:147 -151.
[9]張宏禮,井元偉,張嗣灜.網絡控制系統的主動變采樣控制器設計(英)[J].系統仿真學報,2009,21(22):7275-7280.
[10]VELASCO M,FUERTES J M,LIN C,et al.A control approach to bandwidth management in networked control system[C]//30th Annual Conference of IEEE Industrial Electronics Society,2004.Piscataway:IEEE ,2004:2343 -2348.
[11]GUO G,LU ZB,HAN Q L.Control with Markov sensors/actuators assignment[J].IEEE Transactions on Automatic Control.2012,57(7):1799-1804.
[12]JI K,KIM W.Optimal bandwidth allocation and QoS-adaptive control co-design for networked control systems[C]//ASME 2007 International Mechanical Engineering Congress and Exposition.Washington:ASME,2007:831-839.
[13]LI Z,CHOW M Y.Adaptive multiple sampling rate scheduling of real-time networked supervisory control system-Part I[C]//32nd Annual Conference on IEEE Industrial Electronics,IECON 2006.Piscataway:IEEE,2006:4615-4620.
[14]LI Z,CHOW M Y.Sampling rate scheduling and digital filter co-design of networked supervisory Control system[C]//IEEE International Symposium on Industrial Electronics,2007.Piscataway:IEEE,2007:2893-2898.
[15]熊輝,王耀青.控制理論在擁塞控制中的應用及若干新思路[J].武漢科技大學學報:自然科學版,2002,25(1):68-72.
[16]任敏,王萬良.基于優化控制理論的網絡擁塞控制方法[J].機電工程,2003,20(5):123-126.
[17]WANG Z W,SUN H T.A Bandwidth Allocation Strategy based on the Proportion of Measurement Error in Networked Control System[C]//2012 Third International Conference on Digital Manufacturing and Automation(ICDMA).Piscataway:IEEE,2012:9-12.
[18]鄭大鐘.線性系統理論[M].2版.北京:清華大學,2011:319-324.

