利用Haskind源格林函數(shù)計(jì)算規(guī)則波中航行艦船的繞射興波及壓力分布
黎 昆,張志宏,顧建農(nóng),王 沖
(1.中國(guó)人民解放軍91388 部隊(duì),廣東 湛江524022;2.海軍工程大學(xué),湖北 武漢430033)
0 引 言
艦船在規(guī)則波中航行時(shí),由于入射波浪的作用將會(huì)產(chǎn)生搖蕩運(yùn)動(dòng)。艦船在規(guī)則波中搖蕩的流體動(dòng)力計(jì)算可分成輻射問題和繞射問題分別加以處理。艦船無航速時(shí)(可看作浮體),如果船體搖蕩幅度較小,搖蕩興波也很小,在勢(shì)流理論范圍內(nèi),搖蕩的定解問題就可以線性化。艦船有航速(即使是等速直線運(yùn)動(dòng))之后,其在波浪上運(yùn)動(dòng)的理論分析要比無航速時(shí)復(fù)雜得多,其中最主要的是受航行興波與搖蕩興波的干擾。定常移動(dòng)Kelvin 源格林函數(shù)主要用于解決有航速艦船定常興波問題,而Haskind源格林函數(shù)主要解決波浪中無航速或有航速艦船的搖蕩問題。相對(duì)Kelvin 源格林函數(shù)來說,Haskind源格林函數(shù)的計(jì)算更為復(fù)雜。關(guān)于如何快速準(zhǔn)確計(jì)算Haskind 源格林函數(shù)及其偏導(dǎo)數(shù),不少學(xué)者已對(duì)此進(jìn)行了研究[1-5]。
本文以Wigley 數(shù)學(xué)船型為研究對(duì)象,在理想流體情況下采用微幅波理論,只考慮波浪的繞射問題,通過引入低航速假定來計(jì)算波浪與以定常速度移動(dòng)船體之間的流體動(dòng)力干擾。基于線性勢(shì)流理論,利用無限水深三維移動(dòng)脈動(dòng)源(Haskind 源)格林函數(shù)方法計(jì)算規(guī)則波中航行艦船的繞射興波波形及其對(duì)應(yīng)的一定水深處的壓力場(chǎng)分布。
1 理論分析
1.1 建立坐標(biāo)系和定解方程
需要建立2 個(gè)坐標(biāo)系:1)大地坐標(biāo)系OXYZ,原點(diǎn)O 位于未擾動(dòng)的水面上;2)隨船平動(dòng)的坐標(biāo)系oxyz,原點(diǎn)o 位于未擾動(dòng)的靜水面上,x 軸水平指向船首,z 軸垂直向上,y 軸指向船的側(cè)面,構(gòu)成右手正交系。艦船以固定航速V 沿x 方向行駛,入射波沿-x 方向傳播,入射波傳播方向與x 軸正向之間的夾角為β(迎浪時(shí)β=180°),如圖1所示。
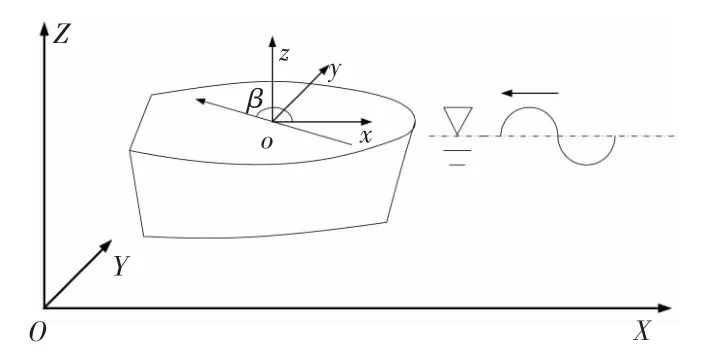
圖1 波浪繞船示意圖Fig.1 Sketch map of wave flow around ship
根據(jù)波浪理論,入射規(guī)則波的一階速度勢(shì)用復(fù)數(shù)形式可表示為:
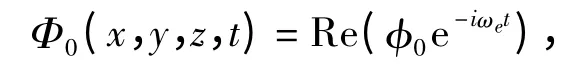
而
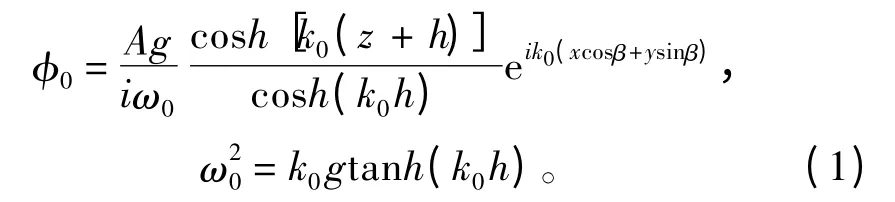
假定艦船運(yùn)動(dòng)響應(yīng)與入射波波幅是同階小量,且經(jīng)過一段時(shí)間后艦船運(yùn)動(dòng)已經(jīng)達(dá)到穩(wěn)定狀態(tài),根據(jù)線性勢(shì)流理論,艦船位移向量將作為以遭遇頻率ωe(ωe=ω0-k0Vcosβ)為變化頻率的簡(jiǎn)諧量。艦船以定常速度V 沿直線運(yùn)動(dòng)時(shí)船體將產(chǎn)生移動(dòng)興波,相對(duì)于隨船平動(dòng)的坐標(biāo)系oxyz 來說,由定常移動(dòng)產(chǎn)生的定常興波速度勢(shì)可表示為-Vx+Φs(x,y,z)。按照線性勢(shì)流理論,艦船周圍流場(chǎng)中的總速度勢(shì)由定常勢(shì)[-Vx+Φs(x,y,z)]和非定常勢(shì)ΦT(x,y,z,t)兩部分組成,如下:
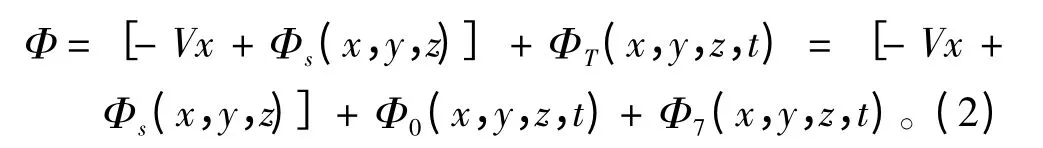
式中:Φs為艦船在靜水中恒速航行時(shí)引起的定常興波勢(shì)(通常假定此部分速度勢(shì)相對(duì)較小,以下忽略其影響);Φ0為已知的入射波速度勢(shì);Φ7為待求的繞射波速度勢(shì)。
由于尋求穩(wěn)態(tài)解,所以采用頻域分析方法把時(shí)間因素和空間因素分離開來,設(shè)繞射勢(shì)Φ7=Re[φ7(x,y,z)eiωet],則無限水深水域中繞射勢(shì)的定解問題可表示為[6]:
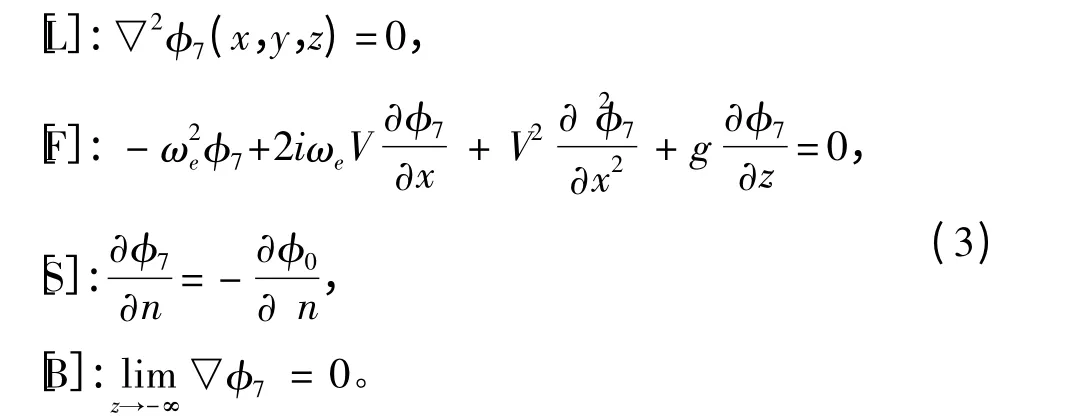
式中:[L],[F],[S],[B]分別為L(zhǎng)APLACE 方程、自由水面邊界條件、物面邊界條件和水底條件;(x,y,z)為場(chǎng)點(diǎn)坐標(biāo);t 為時(shí)間;V 為航速;g 為重力加速度;n 為物面外法線矢量(指向船體外部)。
1.2 定解方程的求解
采用分布源法求解上述定解問題,在船體表面上均勻布置Haskind 源,則場(chǎng)點(diǎn)P(x,y,z)處繞射勢(shì)φ7可表示成積分形式:
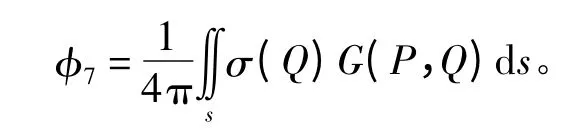
式中:σ(Q)為源點(diǎn)Q(ξ,η,ζ)處的源強(qiáng)密度;G 為Haskind 源格林函數(shù)。
將繞射勢(shì)φ7運(yùn)用于物面條件可得到用來求解源強(qiáng)密度σ 的積分方程,即:
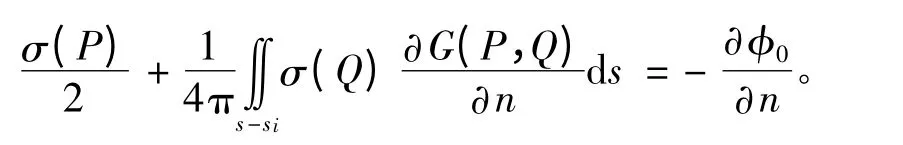
將上述積分方程式進(jìn)行離散化,化成代數(shù)方程組求解[7]。離散方法是把船體表面分成N 個(gè)小面元,在標(biāo)號(hào)為n(n=1,2,…,N)的面元上布置等強(qiáng)度且為常數(shù)的面源σn,并且在每塊小面元上選一控制點(diǎn)Pn,使這些離散的控制點(diǎn)滿足邊界條件。則上述積分方程可離散化成如下代數(shù)方程組:
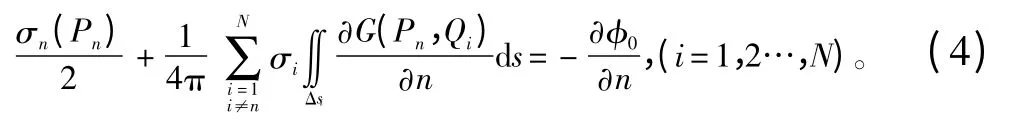
解代數(shù)方程組(4)求出源強(qiáng)σ,即可求出流場(chǎng)中任一點(diǎn)的繞射勢(shì)φ7和速度分布。
1.3 格林函數(shù)中奇點(diǎn)的積分處理
求解源強(qiáng)σ 的關(guān)鍵和難點(diǎn)在于如何準(zhǔn)確、快速地計(jì)算三維移動(dòng)脈動(dòng)源(Haskind 源)格林函數(shù)G(x,y,z;ξ,η,ζ)。該函數(shù)為奇異的二重積分式,求積計(jì)算困難費(fèi)時(shí),被積函數(shù)為復(fù)變函數(shù)且是奇異和振蕩的,并且在有的區(qū)間成為高頻振蕩函數(shù),如果處理不好就會(huì)導(dǎo)致計(jì)算結(jié)果出現(xiàn)較大的誤差甚至失效。該積分表達(dá)式形狀復(fù)雜、處理繁瑣,其表達(dá)式原型為:
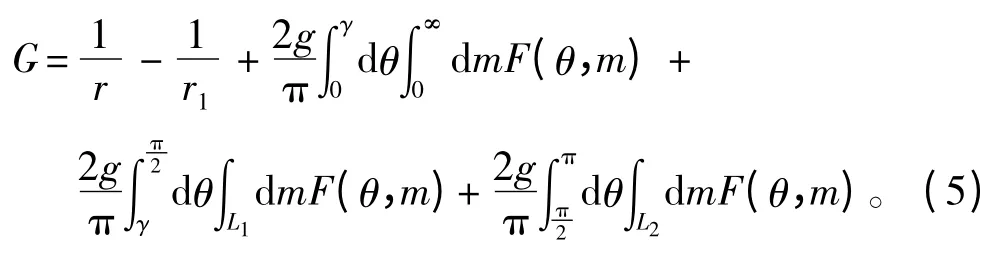
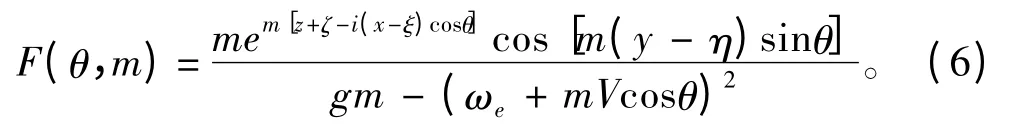
式中:θ 為復(fù)波數(shù)的幅角;m 為復(fù)波數(shù)的幅值;ωe為脈動(dòng)源的振蕩圓頻率;V 為船速;(x,y,z)和(ξ,η,ζ)分別為場(chǎng)點(diǎn)和源點(diǎn)坐標(biāo);g 為重力加速度。
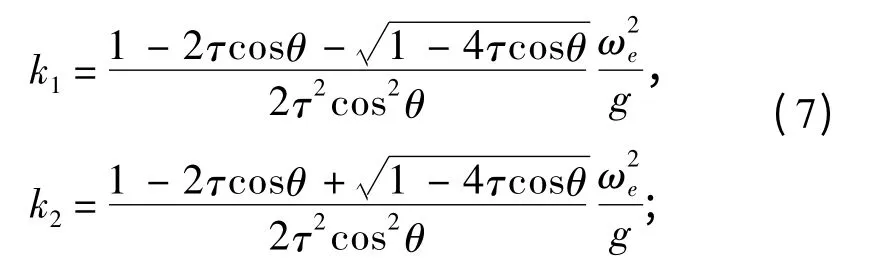
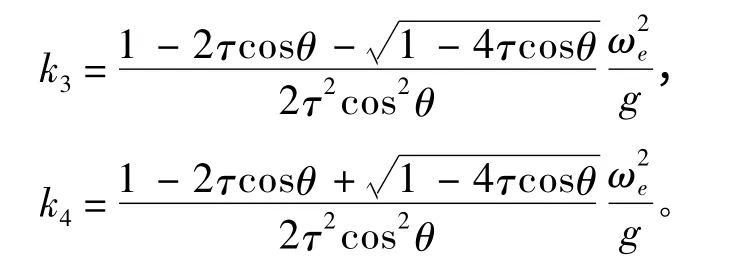
將k3和k4寫成在區(qū)間上的表達(dá)式為:
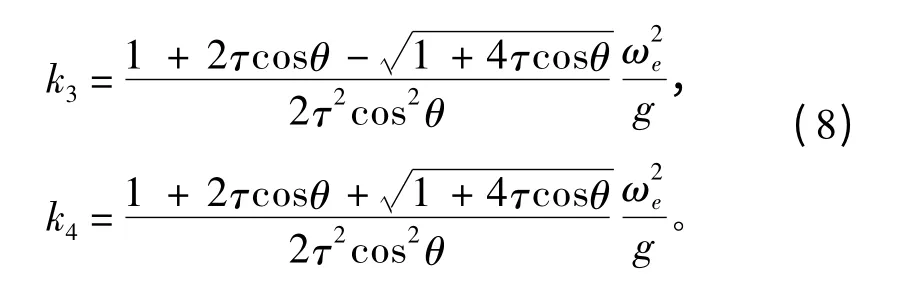
為了使遠(yuǎn)方輻射條件得以滿足,L1和L2分別取為經(jīng)過k1+iε,k2-iε,k3+iε和k4+iε 繞過k1,k2奇點(diǎn)和k3,k4奇點(diǎn)的積分路徑,其中ε 為任意小的正數(shù),積分路徑如圖2和圖3所示。通過整理,被積函數(shù)F(θ,m)可表示為:
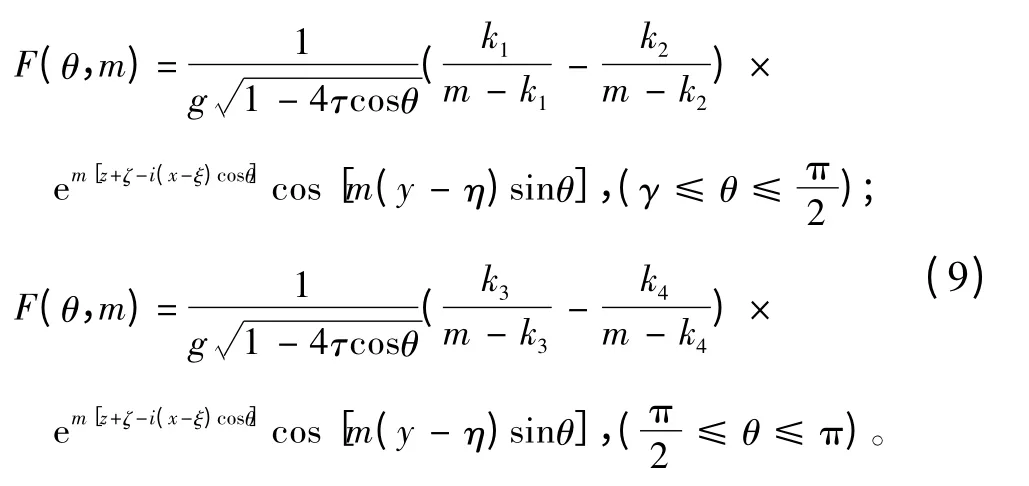
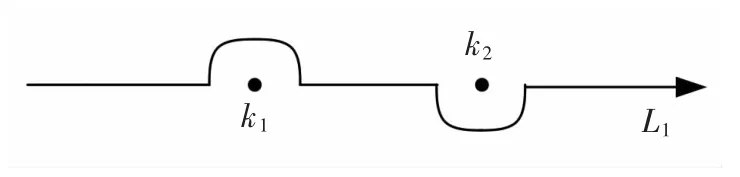
圖2 積分路徑Fig.2 Inteqral path
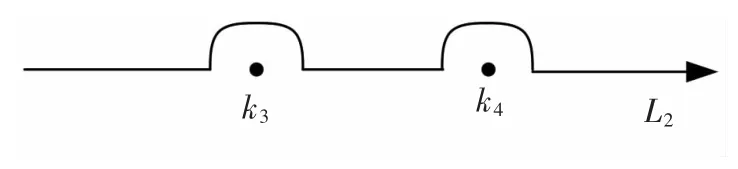
圖3 積分路徑Fig.3 Inteqral path
令:
x1=(z+ζ)+i[-(x-ξ)cosθ+(y-η)sinθ],
x2=(z+ζ)+i[-(x-ξ)cosθ-(y-η)sinθ],
x3=(z+ζ)-i[-(x-ξ)cosθ-(y-η)sinθ],
x4=(z+ζ)-i[-(x-ξ)cosθ+(y-η)sinθ]。
代入式(5)中進(jìn)行整理,則格林函數(shù)G 中第1個(gè)積分項(xiàng)可寫為:
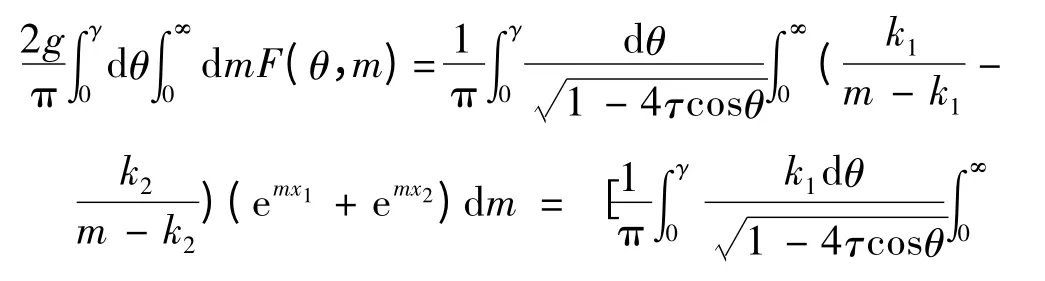
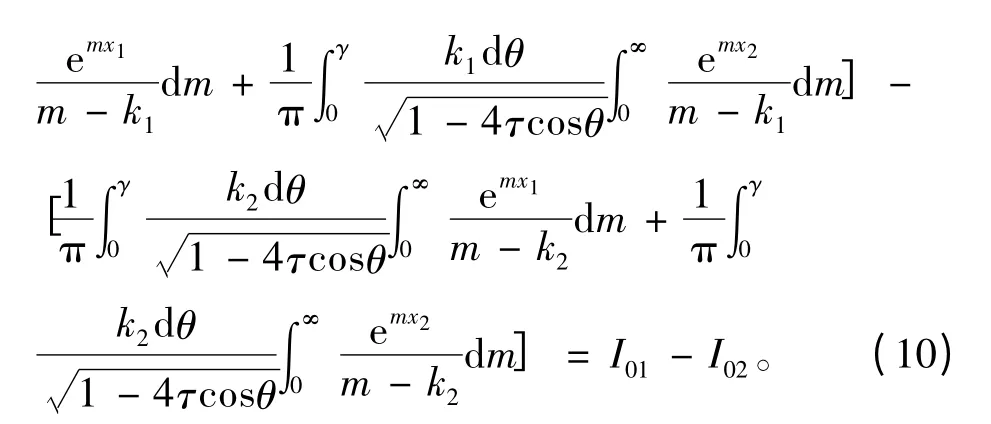
同理,第2 個(gè)積分項(xiàng)可寫為:
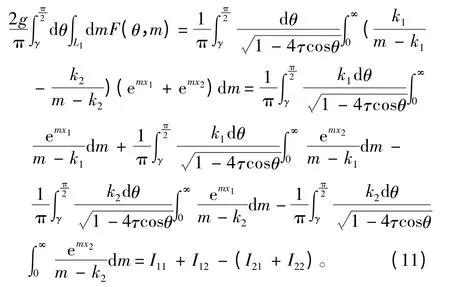
同理,第3 個(gè)積分項(xiàng)可寫為:
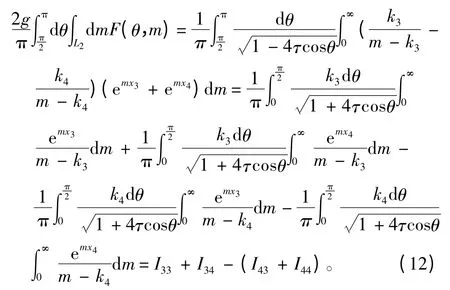
則格林函數(shù)G(x,y,z;ξ,η,ζ)可表示為:
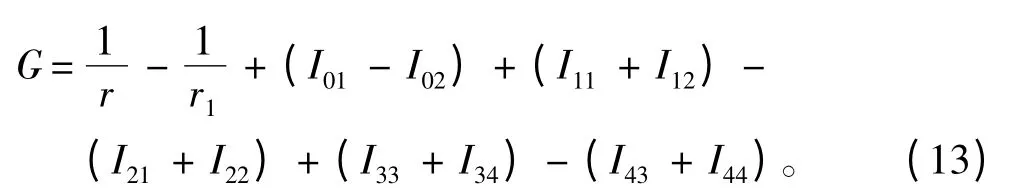
引入復(fù)指數(shù)積分函數(shù)E1(Z)[8]后,Iij的表達(dá)式可整理成單積分的形式:
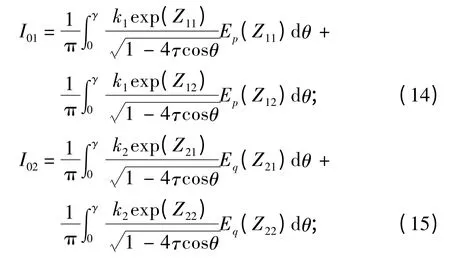
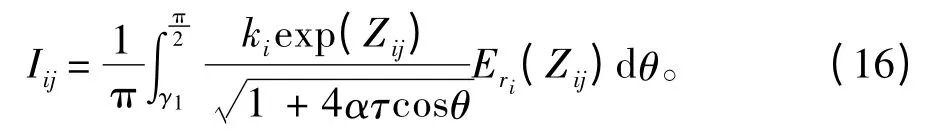
式中:Zij=kixj(i,j=1,2 或i,j=3,4);當(dāng)i=1,2 時(shí),γ1=γ,α=-1;當(dāng)i=3,4 時(shí),γ1=0,α=1。
當(dāng)Re(Z)≥0 時(shí):
Ep(Z)=Eq(Z)=E1(Z);
當(dāng)Re(Z)<0,lm(Z)≥0 時(shí):
Ep(Z)=E1(Z),Eq(Z)=E1(Z)+2πi;
當(dāng)Re(Z)<0,lm(Z)<0 時(shí):
Ep(Z)=E1(Z)-2πi,Eq(Z)=E1(Z);
當(dāng)lm(Z)≥0 時(shí):
Eri(Z)=E1(Z),(i=1,3,4),Eri(Z)=E1(Z)+2πi,(i=2);
當(dāng)lm(Z)<0 時(shí):
Eri(Z)=E1(Z)-2πi,(i=1,3,4),Eri(Z)=E1(Z),(i=2)。

采用上述變換方法利用復(fù)指數(shù)函數(shù)進(jìn)行處理后,Haskind 源格林函數(shù)計(jì)算格式可以成功地處理內(nèi)層積分中的奇點(diǎn)并將二重積分轉(zhuǎn)化成單積分形式,從而解決了被積函數(shù)中奇點(diǎn)的奇異振蕩問題。進(jìn)而采用遞推自適應(yīng)Simpson 法計(jì)算變換后的積分會(huì)容易很多,且積分是收斂的,并可以大大地減少計(jì)算時(shí)間。
2 繞射興波及壓力場(chǎng)的計(jì)算
解決了Haskind 源格林函數(shù)中的奇點(diǎn)問題,即可求解出規(guī)則波對(duì)以恒定速度航行于其中的艦船引起的繞射勢(shì)、繞射興波波形以及水底壓力變化。由船舶興波理論知識(shí)可知繞射興波的表面波形為:
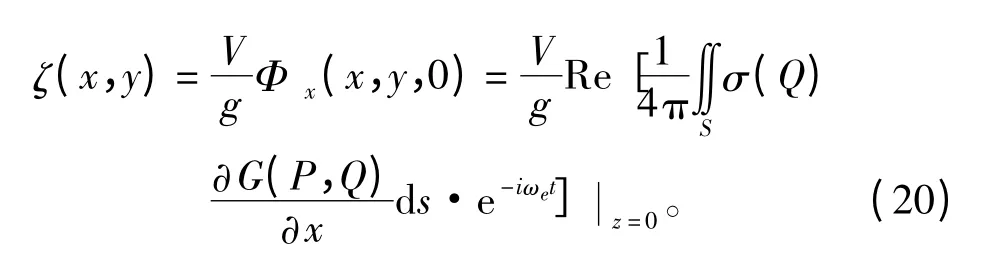
上式中對(duì)格林函數(shù)G(x,y,z;ξ,η,ζ)求偏導(dǎo),只需對(duì)被積函數(shù)F(θ,m)求偏導(dǎo)即可。
由總速度勢(shì)的分解式(2)可得到距離水面任意點(diǎn)處脈動(dòng)壓力表達(dá)式為:
P(x,y,z,t)=Re[p(x,y,z)·e-iωet]。
式中p(x,y,z)=p0(x,y,z)+p7(x,y,z)。
根據(jù)伯努利方程,由式(1)可得入射波脈動(dòng)壓力為:
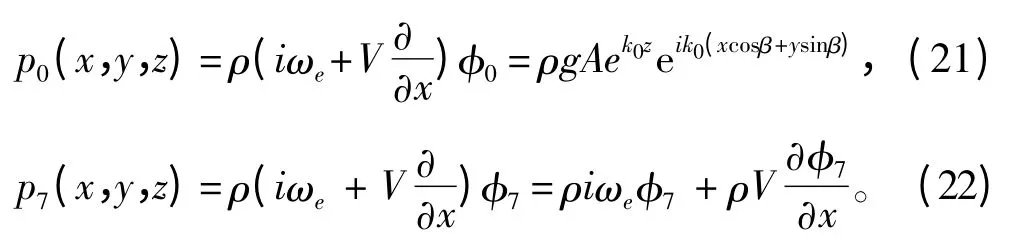
式中:p0為入射波壓力;p7為繞射波壓力。
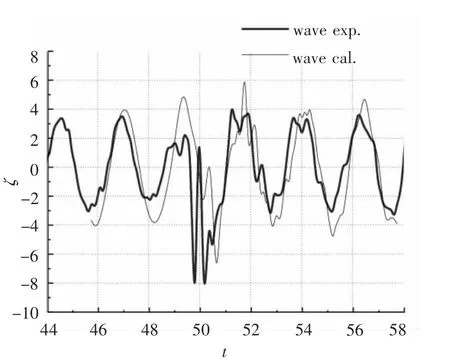
圖4 波形計(jì)算結(jié)果與實(shí)驗(yàn)結(jié)果比較(T0=2.353 s,V=1.0 m/s)Fig.4 Comparison between computed and experimental results of wave pattern when T0=2.353s,V=1.0m/s
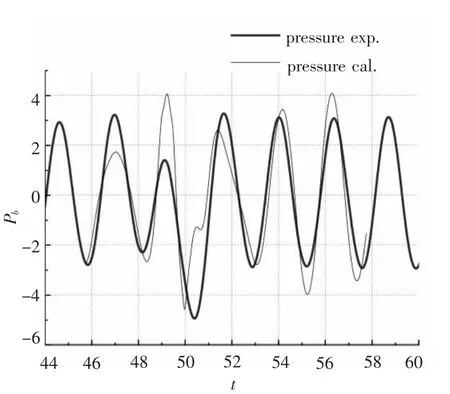
圖5 壓力計(jì)算結(jié)果與實(shí)驗(yàn)結(jié)果比較(T0=2.353 s,V=1.0m/s)Fig.5 Comparison between computed and experimental results of pressure when T0=2.353s,V=1.0m/s
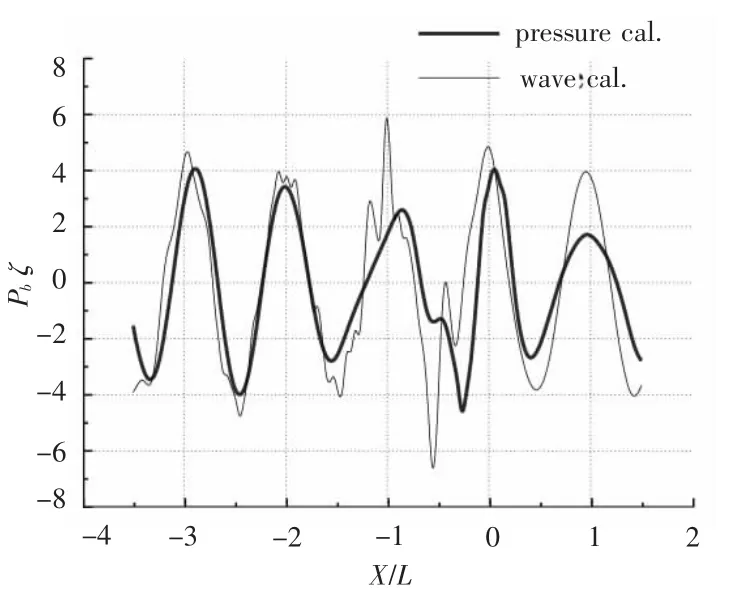
圖6 計(jì)算波形與對(duì)應(yīng)壓力比較(T0=2.353 s,V=1.0 m/s)Fig.6 Comparison between computed wave pattern and it′s corresponding pressure when T0=2.353s,V=1.0m/s
設(shè)定初始參數(shù),利用編制程序計(jì)算得到橫距y=0.25 L 處的繞射波波形、入射波與繞射波的疊加波形及其分別對(duì)應(yīng)的水深h=0.2 L(L 為船長(zhǎng))處的壓力變化。在傅汝德數(shù)Fh≤0.3 的條件下,設(shè)定入射波波幅為3.8 mm,波周期T0=2.353 s,船速V=1.0 m/s,計(jì)算得到繞射波與入射波的疊加波形及其對(duì)應(yīng)的壓力變化與實(shí)驗(yàn)結(jié)果比較的曲線,如圖4 ~圖6所示。圖4和圖5 中船體位置在(t ≤50 s)附近處,而圖6 中船首在(x/L=0.5)處。圖中橫坐標(biāo)表示記錄的時(shí)間t/s,縱坐標(biāo)表示波高及其引起的水底壓力變化ζ,pb(mm H2O)。
另外,在其他條件不變的情況下,改變初始條件,給定入射波波幅為5 mm,波周期T0=2.36 s,船速V=0.8 m/s,利用程序計(jì)算得到的波形和壓力曲線如圖7 ~12所示。圖7和圖8 中船體位置在(t ≤43 s)附近處,而圖9 ~12 中船首在(x/L=0.5)處。
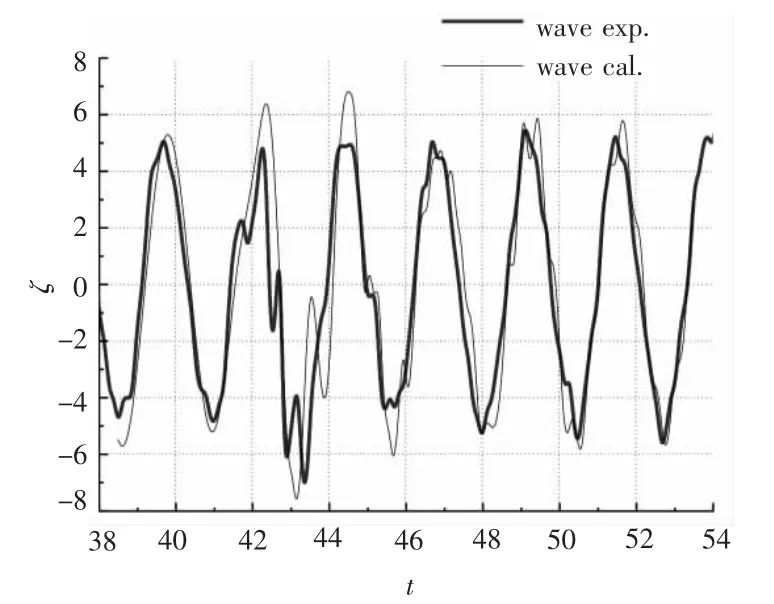
圖7 波形計(jì)算結(jié)果與實(shí)驗(yàn)結(jié)果比較(T0=2.36 s,V=0.8 m/s)Fig.7 Comparison between computed and experimental results of wave pattern when T0=2.36s,V=0.8m/s
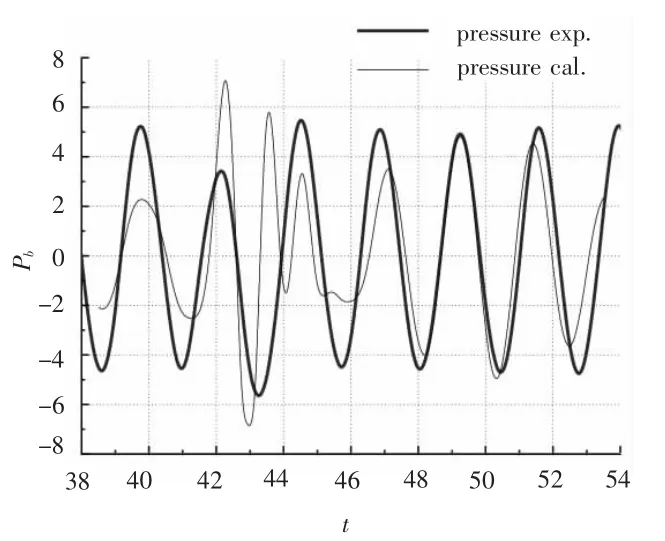
圖8 壓力計(jì)算結(jié)果與實(shí)驗(yàn)結(jié)果比較(T0=2.36 s,V=0.8 m/s)Fig.8 Comparison between computed and experimental results of pressure when T0=2.36s,V=0.8m/s
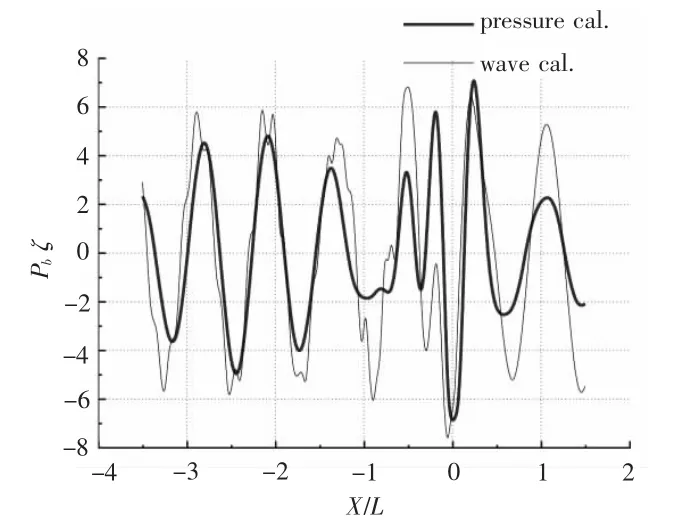
圖9 計(jì)算波形與對(duì)應(yīng)壓力比較(T0=2.36 s,V=0.8 m/s)Fig.9 Comparison between computed wave pattern and it′s corresponding pressure when T0=2.36s,V=0.8m/s

圖10 計(jì)算波形三維分布圖(T0=2.36 s,V=0.8 m/s)Fig.10 Three-dimensional distribution figure of computed wave pattern when T0=2.36s,V=0.8m/s
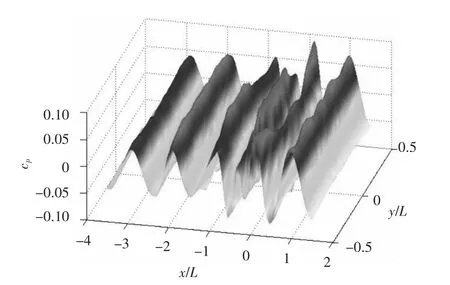
圖11 水深h=0.2 L 處壓力場(chǎng)三維分布圖(T0=2.36 s,V=0.8 m/s)Fig.11 Three-dimensional distribution figure of hydrodynamic pressure field when h=0.2L,T0=2.36s,V=0.8m/s
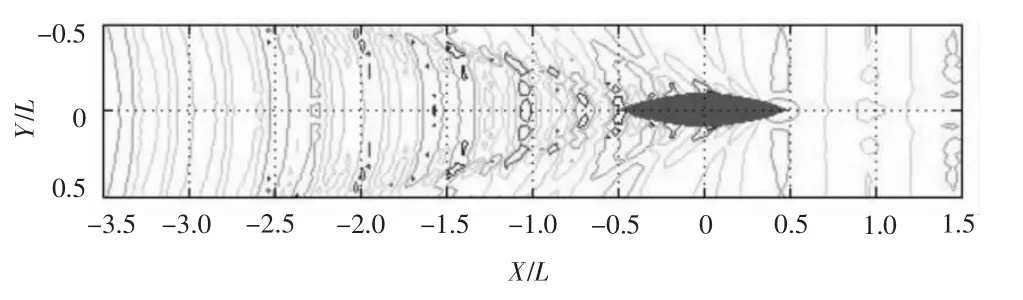
圖12 計(jì)算波形等高線圖(T0=2.36 s,V=0.8 m/s)Fig.12 Computed wave contour line when T0=2.36s and V=0.8m/s
將繞射波與入射波疊加波形的計(jì)算結(jié)果和完成的實(shí)驗(yàn)結(jié)果進(jìn)行對(duì)比,發(fā)現(xiàn)二者基本吻合,趨勢(shì)一致,如圖4和圖7所示。疊加后的波形在水底引起的壓力變化與實(shí)驗(yàn)結(jié)果相比有一定的誤差,這是因?yàn)閷?shí)驗(yàn)結(jié)果測(cè)量的是艦船航行、船體興波、入射波和繞射波等因素共同作用引起的水底壓力變化,而計(jì)算結(jié)果只考慮了入射波和繞射波的作用,忽略了艦船航行及船體興波等因素的影響,因此計(jì)算結(jié)果和實(shí)驗(yàn)結(jié)果之間會(huì)有所差別,但差別不大,如圖5和圖8所示。因?yàn)榈透等甑聰?shù)條件下,艦船航行及船體興波引起的水底壓力變化相對(duì)為一小量,可忽略不計(jì)。在船頭前方(x/L=1,-0.3 ≤y/L ≤0.3)附近繞射波形及其對(duì)應(yīng)壓力出現(xiàn)了峰谷不對(duì)應(yīng)現(xiàn)象,此時(shí)入射波遇到艦船會(huì)產(chǎn)生反射,入射波、繞射波、反射波相互影響使船前會(huì)出現(xiàn)一定范圍的雜波,如圖10 ~圖12所示。
3 結(jié) 語
以上理論和實(shí)驗(yàn)研究驗(yàn)證了本文對(duì)Haskind 源格林函數(shù)中奇點(diǎn)的積分處理方法和編制程序的正確性。在此基礎(chǔ)上,改變定解方程滿足的物面條件可深入研究航行艦船各個(gè)模態(tài)輻射勢(shì)的水動(dòng)力計(jì)算,并可以進(jìn)一步推廣計(jì)算隨機(jī)波中航行艦船輻射勢(shì)和繞射勢(shì)引起的水中任一定深處的壓力變化。
[1]WAKELING B P,SPROSTON J L,MILLWARD A.Development of a theoretical model of the pressure distribution on a ronnd bilge hull[J].J.S.R,1986,30(1).
[2]陶建華,吳巖.三維布源法計(jì)算大尺度物體波浪力中奇點(diǎn)積分的處理[J].水動(dòng)力學(xué)研究與進(jìn)展,1987,2(4):16-22.
TAO Jian-hua,WU Yan.The treatment of singular integrals in the calculation of wave forces acting on a large scale structure with 3- D source distribution method[J].Journal of Hydrodynamics,1987,2(4):16-22.
[3]WU G X,TAYLOR R E.A green′s function form for ship motions at forward speed[J].International Shipbuilding Progress,1987,34(398):189-196.
[4]宗智,黃鼎良.三維移動(dòng)脈動(dòng)源速度勢(shì)的數(shù)值研究[J].水動(dòng)力學(xué)研究與進(jìn)展,1991(6):55-63.
ZONG Zhi,HUANG Ding-liang.Numerical studies on potential of a 3-D pulsating source in uniform stream[J].Journal of Hydrodynamics,1991(6):55-63.
[5]盧曉平,葉恒奎,張緯康,等.Haskind 源格林函數(shù)的奇異性研究與數(shù)值積分方法[J].水動(dòng)力學(xué)研究與進(jìn)展,1999,14(4):444-452.
LU Xiao-ping,YE Heng-kui,ZHANG Wei-kang,et al.The study on singularity of Haskind-Source Green′s Function and related method of numerical integration.Journal of Hydrodynamics,1999,14(4):444-452.
[6]劉應(yīng)中,繆國(guó)平.船舶在波浪上的運(yùn)動(dòng)理論[M].上海:上海交通大學(xué)出版社,1987.
LIU Ying-zhong,MIAO Guo-ping.Theory of ship motion in waves[M].Shanghai:Shanghai Jiaotong University Press,1987.
[7]黎昆,張志宏,顧建農(nóng),等.利用面元法計(jì)算艦船在水底引起的壓力分布[J].海軍工程大學(xué)學(xué)報(bào),2011,23(1):43-46.
LI Kun,ZHANG Zhi-hong,GU Jian-nong,et al.Calculating pressure distribution on water bottom caused by a moving ship with panel method[J].Journal of Naval University of Engineering,2011,23(1):43-46.
[8]MILTON A,IRENE A S.Handbook of mathematical functions with formulas,graphs,and mathematical tables[M].National Bureau of Standards,Applied Mathematics Series 55,Issued June 1964,F(xiàn)ourth Printing,December 1965,With Corrections.

