與非合作目標交會的追蹤衛星軌道L2－L∞增益控制

鄧 泓 孫兆偉 仲惟超 張 健

1. 上海衛星工程研究所，上海200240

2. 哈爾濱工業大學衛星技術研究所，哈爾濱150001

3. 北京空間飛行器總體設計部，北京100094

空間非合作目標是指一類不能提供有效合作信息的空間飛行物，包括故障或失效衛星、空間碎片和對方衛星等［1］。與這類空間非合作目標進行交會是完成在軌服務、空間垃圾清除和空間攔截等空間任務的基礎［2］。當追蹤衛星與對方衛星這類空間非合作目標交會時，目標衛星為了逃避追蹤可能存在軌道機動。本文主要針對這類情況的空間交會，研究了追蹤衛星的軌道控制方法。

隨著推力可連續變化推進器的出現，基于控制理論的變推力軌道控制方法逐漸取代傳統的沖量式軌道控制方法，成為近年來研究熱點，如文獻［3 －4］分別采用自適應控制和滑模控制方法為空間交會設計了軌道控制器。這類方法通常可對系統的穩定性進行設計和分析，因而具有更高的控制精度。當目標衛星存在軌道機動時，傳統的Hill 方程或是橢圓相對軌道方程不再適用。為此，本文建立了在慣性系下描述的相對軌道近似模型。由于目標衛星的非合作性，其軌道機動的大小是不可測得的，故本文將目標衛星軌道機動處理成系統干擾。為了抑制干擾，通常可采用魯棒控制器，如文獻［5］研究了系統存在控制輸入干擾時追蹤衛星的魯棒H∞軌道控制方法;文獻［6］考慮了干擾對系統輸出的L2增益，提出了一種自適應飛行控制方法;文獻［7］進一步研究了存在參數不確定性和控制干擾時的最優控制。此外，執行器的輸出一般都有幅值，即具有飽和特性。若不考慮該特性可能導致控制器在實際應用中精度降低甚至失效。因而有必要研究系統在該特性下仍能漸近穩定的控制器設計方法，如文獻［8 －9］均針對控制輸入受限下的航天器姿態調節和姿態機動控制問題提出了相應的控制器設計方法。由于這類任務的快速性要求，可考慮系統的有限時間性能，如文獻［10］中以系統有限時間性能為優化指標進行控制器的設計。

本文綜合考慮上述所有條件，以系統有限時間性能為優化指標，提出了L2－L∞增益控制器設計方法，并基于線性不等式(Linear Matrix Inequality，LMI)技術證明了采用該控制器的閉環系統在執行器飽和特性下是漸近穩定的。

1 相對軌道模型

在地心慣性坐標系中［11］，目標衛星和追蹤衛星的軌道動力學方程分別為:

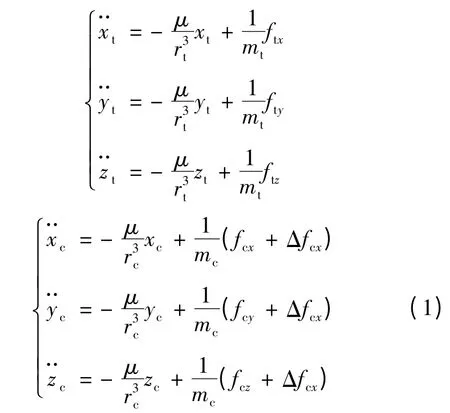
式中，μ 為地球引力常數，x，y，z 為衛星在慣性系中的位置，r 表示衛星地心距，m 表示衛星質量，f 表示衛星軌道控制力，Δf 表示干擾力量，下標“t”代表目標衛星，下標“c”代表追蹤衛星。

令xe，ye，ze表示兩星相對位置在慣性系下的分量，假設兩星的相對距離遠遠小于它們的地心距，則有

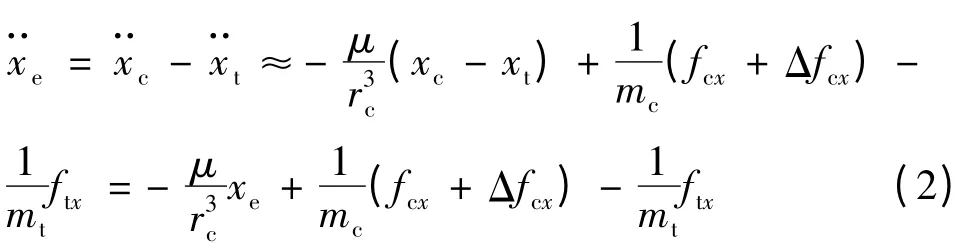
同理，對另兩軸同樣有下式成立:

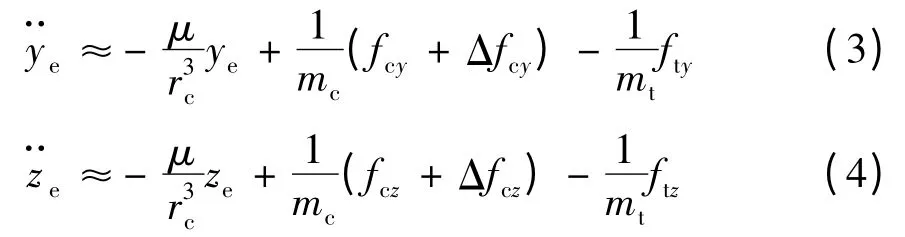
在追蹤衛星逐漸逼近目標衛星的過程中，其地心距rc是時變參數。因此將式(2 ～4)中包含rc的時變參數分成2 部分:1)時不變的參數;2)時變參數，可視作模型的不確定性，即

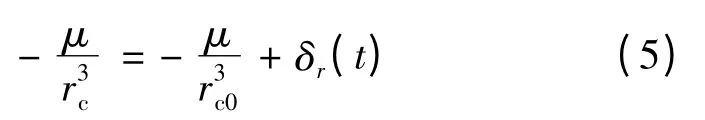
式中，rc0為初始時刻追蹤衛星的軌道半徑，δr(t)為由軌道半徑變化引起的時變參數，滿足表示其變化幅值。

由于目標衛星的非合作性，其軌道控制力的變化是無法測得的，于是將目標衛星的軌道控制力視作模型的擾動。令系統狀態向量、軌道控制力向量、測量輸出向量和干擾向量分別為:

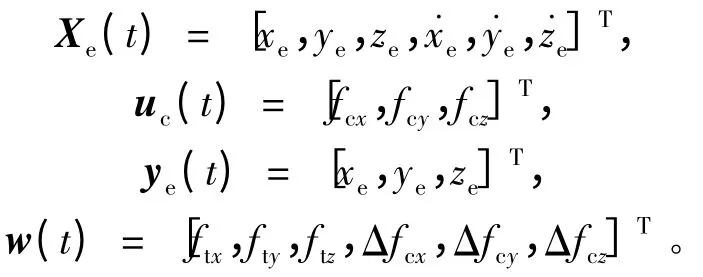
并考慮追蹤衛星和目標衛星質量的不確定性:

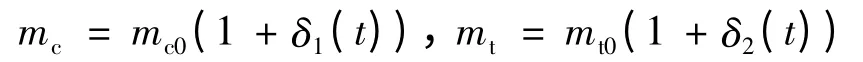
式中，mc0，mt0為質量的初始值，δ1(t)，δ2(t)分別滿足和為幅值。

結合式(1 ～5)，則系統模型可寫為:

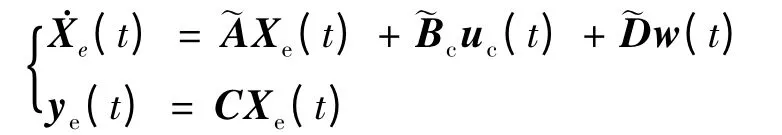
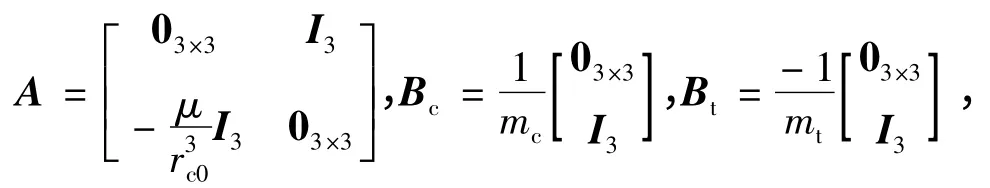
In表示維數為n 的單位陣，0m×n表示維數為m × n的零矩陣。不確定部分ΔA(t)，ΔBc(t)和ΔD(t)具有如下形式:

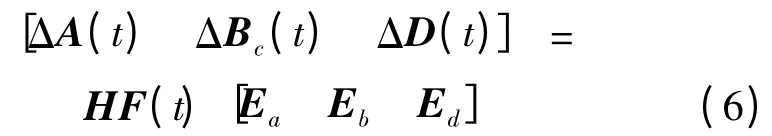
式中，H =［H0H0H0H0］，H0=［03×3I3］T，

可見，FT(t)F(t)≤I。

在實際應用中，衛星軌道推進器的推力通常都有幅值，即具有飽和特性。考慮該特性:

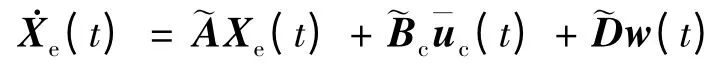
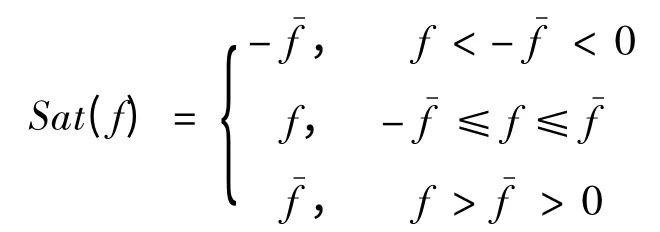
本文采用狀態反饋控制即uc(t)= KXe(t)，K為控制增益陣。故閉環系統可寫為:

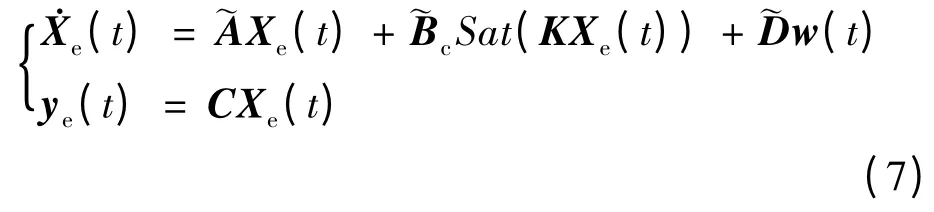
2 L2 －L∞增益控制器設計

2.1 控制器設計目標

為抑制干擾對系統的影響，本文考慮了系統的L2－ L∞增益，即能量－ 峰值(Energy － to － Peak，EP)增益，其具體定義如下:

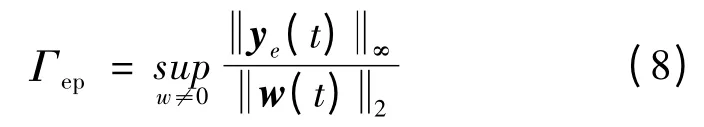
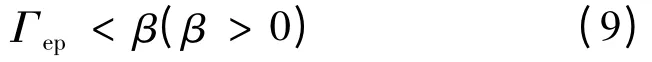
上式等價于，在零初始條件下 ye(t)∞≤β w(t)2。

當追蹤衛星執行與非合作目標衛星的交會任務時，通常要求它能在燃料有限的情況下于有限時間內完成。因此，考慮有限時間內系統狀態和控制輸入向量的線性二次型性能:

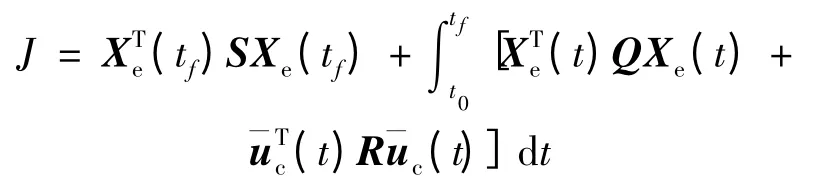
式中，S，Q 和R 均為正定對稱矩陣，t0和tf分別表示初始時刻和終端時刻。

因此，本文控制器設計目標可描述為:針對不確定飽和系統(7)，設計控制增益陣K，使得閉環系統漸近穩定、系統的EP 增益滿足約束(9)且系統的有限時間性能J 達極小值。

2.2 控制器設計

為證明后文提出的定理，給出以下引理。

引理1［12］:設a，b 為具有相同維數的向量，對于具有相應維數的任意矩陣Γ 滿足ΓTΓ ≤I，則有2aTΓb ≤aTa + bTb。

引理2［12］:設M 和N 為實數矩陣，則對任意矩陣Γ 滿足ΓTΓ ≤I，存在實數ε ＞0 滿足MΓN +NTΓTMT≤ε－1MMT+ εNTN。

定理1 考慮不確定飽和系統(7)，如果存在正定對稱矩陣P 滿足

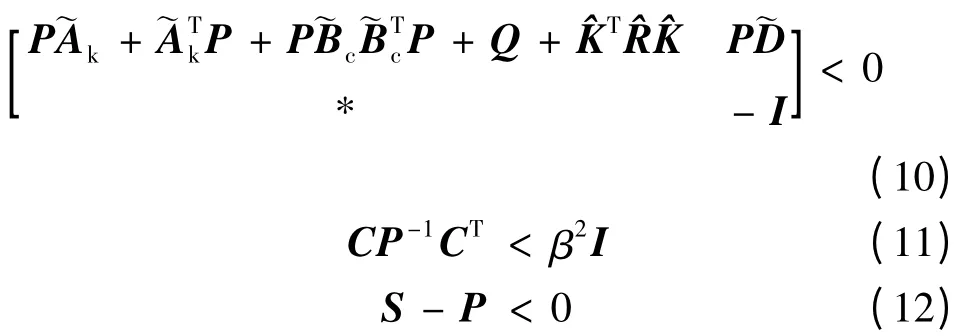
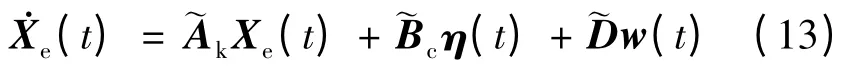
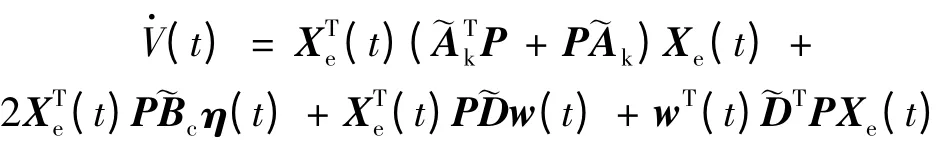
由引理1 可知:

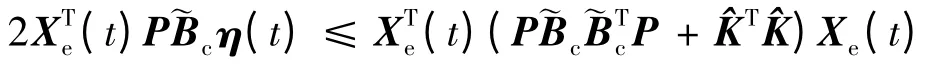
故當w(t)= 0 時，

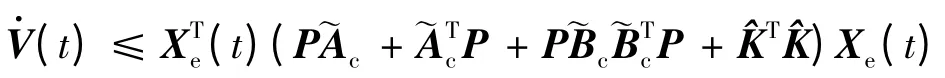
對于有限時間性能J，當R 為對角陣時有

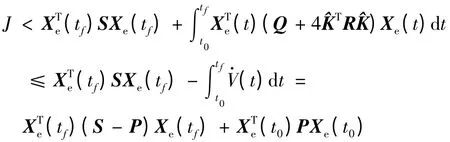
當w(t)≠0 時有:

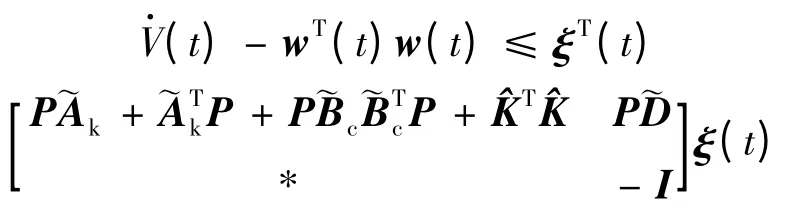
式中:ξT(t)= ［XT(t) wT(t)］。則由式(10)可知，(t)－ wT(t)w(t)＜0 。對該式從0 到τ 積分

并利用零初始條件，可得:

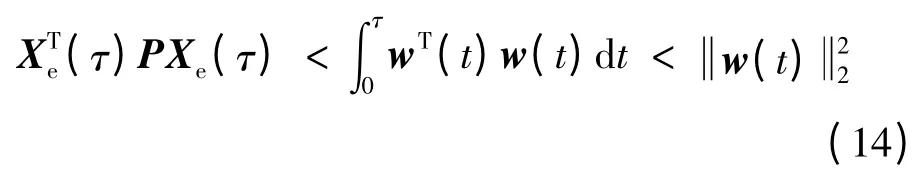
定理2 :考慮不確定飽和系統(7)，如果存在實數β ＞0，μ ＞0，α ＞0，正定對稱矩陣Ω 和矩陣Ψ 滿足

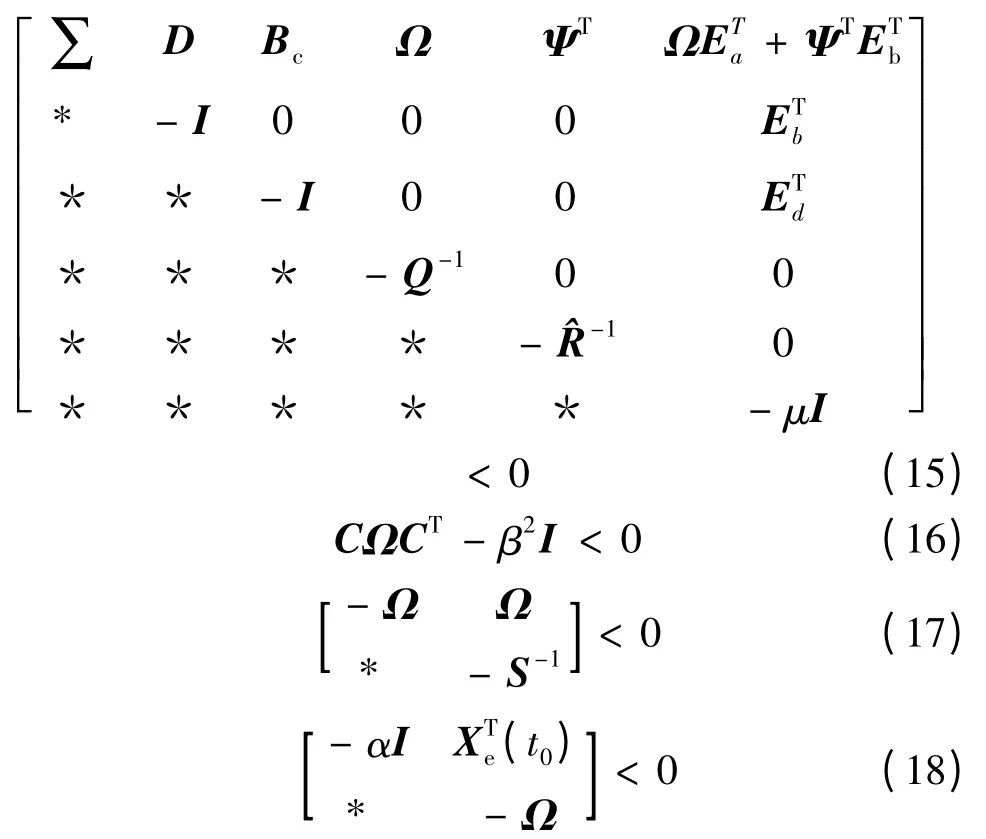
式中，∑= AΩ+ΩAT+BcΨ++μHHT。則存在控制增益陣K 使該系統漸近穩定、系統的EP增益滿足式(9)、有限時間性能J 有上界J ＜α，且控制增益陣K 可由下式計算:

證明:定義Ω = P－1，Ψ =。由定義可知式(16)和(19)均成立。用矩陣J1= diag(Ω，I)對式(10)做全等變換并利用Schur 補定理［9］，則有:

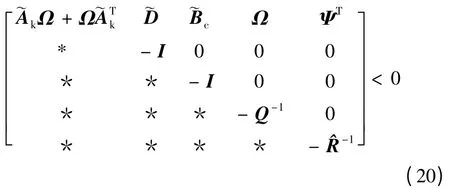
將不確定結構(6)代入上式可得，

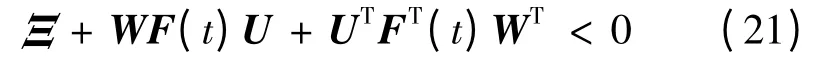
式中，

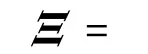
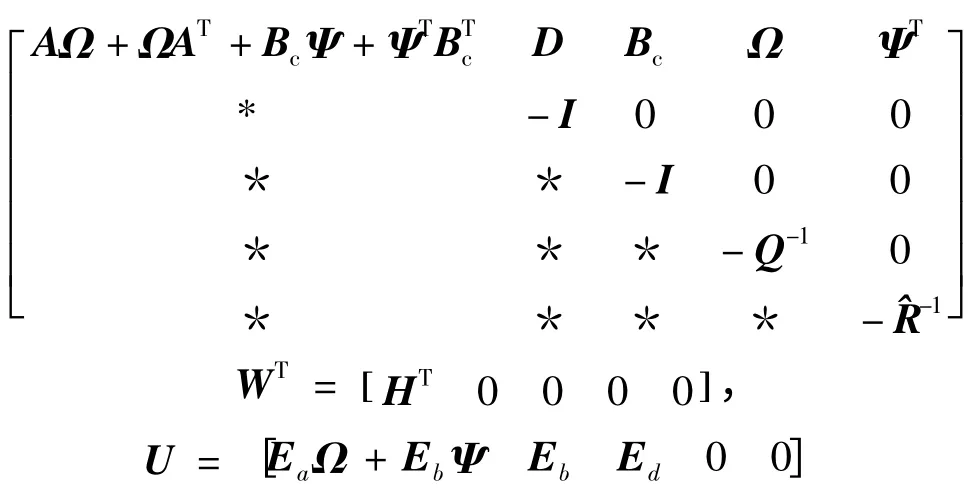
由引理3 知，存在實數μ ＞0 ，使得當式(15)成立時式(21)成立，即式(15)成立時式(10)必然成立。用矩陣Ω 對式(12)做全等變換并利用Schur補定理可得到式(17)。根據Schur 補定理式(18)等價于(t0)PXe(t0)＜α，故性能J 有上界α。

推論1 求解如下凸優化問題可獲得有限時間性能的最優值和控制增益陣:

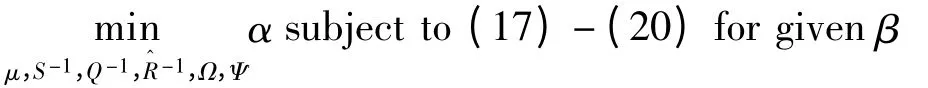
即對于給定β 尋找滿足不等式(17)～(20)的實數μ和矩陣S－1，Q－1，^R－1，Ω，Ψ 使得α 值最小。

3 仿真分析

追蹤衛星質量為500kg，其不確定度為0.1，執行器推力幅值為500N，初始軌道參數見表1。目標衛星質量為500kg，其不確定度為0.1，執行器推力幅值為100N，初始軌道參數見表1。追蹤衛星相對目標衛星的初始相對軌道狀態為(42.00，11.15，－72.48)km 和(－68.68，－32.32，－43.78)m/s。模型的不確定度為

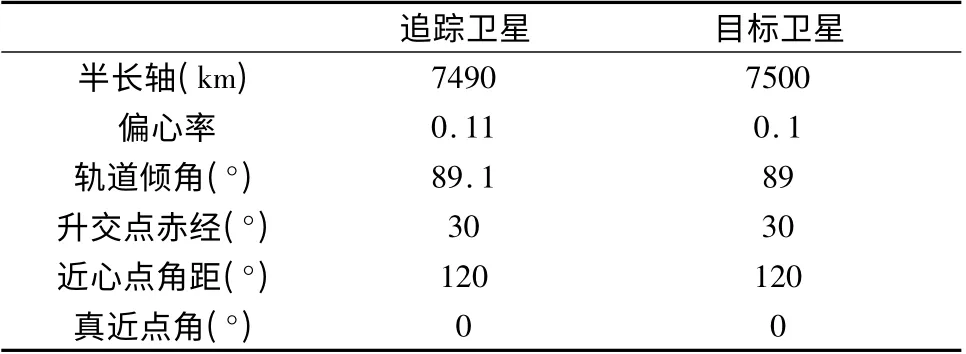
表1 追蹤衛星和目標衛星軌道參數

給定系統的EP 增益為β = 0.1 ，利用MATLAB中的LMI 工具箱求解推論1，可得:

則由式(47)計算可得控制增益陣:

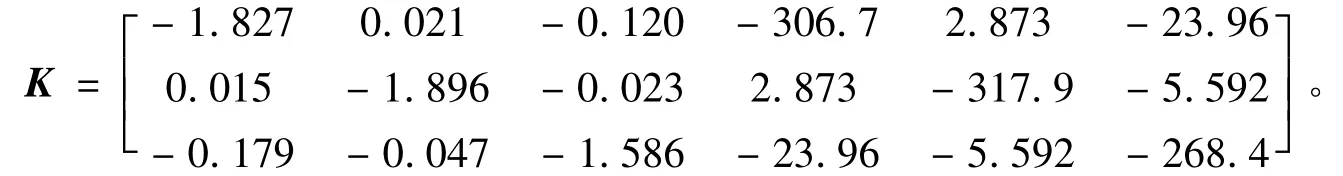
仿真中，給定追蹤衛星的控制干擾始終為控制輸入的10%，目標衛星軌道推力在1000s 內的輸出程正弦變化，即

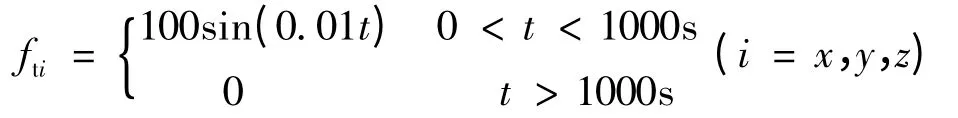
根據上述仿真參數和設計的控制器，可得仿真結果如圖1 ～3 所示。圖1 為追蹤衛星三軸控制輸入的變化圖。在仿真初期，2 星相對位置較大，理論計算的控制輸入也大。由于推進器的飽和特性，實際的控制輸入一直為推進器的推力幅值;隨著追蹤衛星逐漸逼近目標衛星，當理論計算的控制輸入小于推進器幅值時，實際的控制輸入就等于理論計算的控制輸入。圖2 和3 分別為相對位置和相對速度變化圖。由圖可知，相對位置和相對速度均快速收斂，2000s 時控制精度分別為1.7m 和0.01m/s。由以上仿真結果可知，當目標衛星存在軌道機動時，對于帶飽和執行器追蹤衛星的軌道控制，本文設計的控制器是有效的。

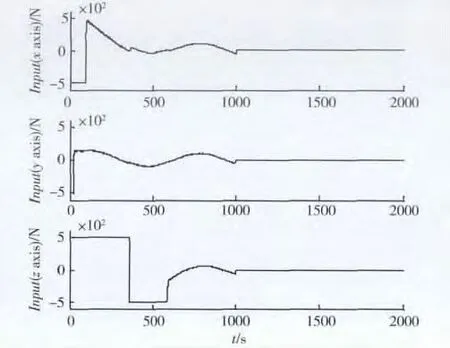
圖1 追蹤衛星三軸控制輸入

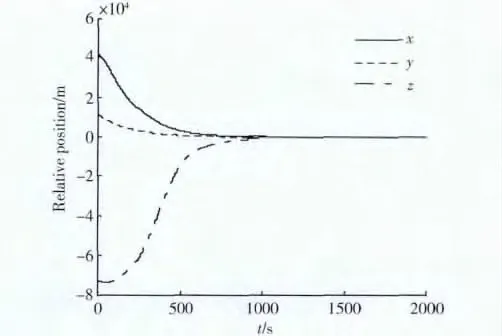
圖2 相對位置

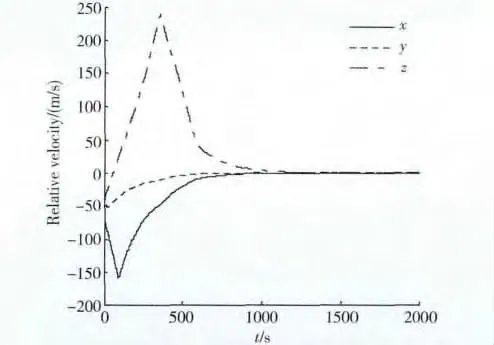
圖3 相對速度

為進一步驗證本文設計的控制器對參數不確定性以及干擾的魯棒性，在仿真中令追蹤衛星和目標衛星質量的不確定度均增大為0.5，追蹤衛星的控制干擾增大為控制輸入的30%，目標衛星的推力幅值增大為150N。仿真結果表明，相對位置和速度仍能快速收斂并穩定，且2000s 時的控制精度分別為2.1m 和0.013m/s。可見，本文設計的控制器對參數不確定性和干擾具有較好的魯棒性。

4 結論

考慮參數不確定性和推進器的飽和性，將非合作目標衛星的軌道機動視作系統干擾，以燃料消耗和時間為優化指標，提出了一種適用于追蹤衛星的L2－L∞增益軌道控制器設計方法。仿真結果表明，當目標衛星存在未知軌道推力時，系統能快速收斂并穩定，對系統的不確定性和干擾具有較好的魯棒性，且控制器結構簡單，便于工程實現。本文研究的干擾為能量有界時的控制器設計方法，為進一步提高控制器的適用范圍，未來可研究干擾為幅值有界時的控制器設計方法。

［1］車汝才，張洪華. 追蹤衛星跟蹤空間非合作目標的相對軌道設計［J］. 航天控制，2006，24(5):40-45.(Che Rucai ，Zhang Honghua. Relative Orbit Design of a Chaser Tracking a Non-cooperative Target in Space［J］. Aerospace Control，2006，24(5):40-45.)

［2］Zhang Dawei，Song Shenmin，Pei Run. Safe Guidance for Autonomous Rendezvous and Docking with a Noncooperative Target［C］. AIAA Guidance，Navigation，and Control Conference，Toronto，2010.

［3］P Singla，K Subbarao，J L Junkins. Adaptive Output Feedback Control for Spacecraft Rendezvous and Docking under Measurement Uncertainty［J］. Journal of Guidance，Control，and Dynamics，2006，29(4):892-902.

［4］B Ebrahimi，M Bahrami，J Roshanian. Optimal Sliding-mode Guidance with Terminal Velocity Constraint for Fixed-Interval Propulsive Maneuvers［J］. Acta Astronautica，2008，60(10):556-562.

［5］Gao Huijun，Yang Xuebo，Shi Peng. Multi-Objective Robust H∞Control of Spacecraft Rendezvous［J］.IEEE Transactions on Control Systems Technology，2009，17(4):794-802.

［6］Yang BongJun，Yucelen Tansel，Shin JongYeob，Anthony J. Calise. An LMI-based Analysis for Adaptive Flight Control with Unmodeled Input Dynamics［C］.AIAA Guidance，Navigation，and Control Conference，Toronto，2010.

［7］黃靜，劉剛，馬廣富. 含不確定性的繩系衛星姿態的魯棒最優控制［J］. 宇航學報，2012，33(10):1423-1431.(Huang Jing，Liu Gang，Ma Guangfu. Nonlinear Robust Optimal Attitude Tracking of Tethered Satellite System with Uncertainties［J］. Journal of Astronautics，2012，33(10):1423-1431.)

［8］Imran Ali，Gianmarco Radice，Jongrae Kim. Backstepping Control Design with Actuator Torgue Bound for Spacecraft Attitude Maneuver［J］. Journal of Guidance，Control，and Dynamics，2010，33(1):254-259.

［9］王景，劉良棟，李果. 控制輸入受限情況下衛星姿態的魯棒自適應控制［J］. 宇航學報，2006，27(4):588-593.(Wang Jing，Liu Liangdong，Li Guo. Robust Adaptive Attitude Control of Satellite Under Control Input Saturation［J］. Journal of Astronautics，2006，27(4):588-593.)

［10］李四平，劉錦陽，國鳳林，許金泉. 軌道機動的時間能量綜合最優控制［J］. 宇航學報，2010，31(1):137-142. (Li Siping，Liu Jinyang，Guo Fenglin，Xu Jinquan. Time-Energy Comprehensive Optimal Control of Orbital Maneuvering［J］. Journal of Astronautics.2010. 31(1):137-142.)

［11］徐光延，項峰，諶穎. 高階帶諧攝動下衛星相對運動精確動力學模型［J］. 宇航學報，2012，33(9):1203-1209.(Xu Guangyan，Xiang Feng，Chen Ying. Exact Dynamic Model of Satellite Relative Motion under Arbitrary Zonal Harmonic Perturbations［J］. Journal of Astronautics，2012，33(9):1203-1209.)

［12］俞立. 魯棒控制——線性矩陣不等式［M］. 北京:清華大學出版社，2002:25-26. (Yu Li. Robust Control:Linear Matrix Inequality［M］. Beijing:Tsinghua University Press，2002:25-26.)