桅桿纖繩水平距離計算
金振鵬,郝康,楊道育
(中通鐵塔(北京)工程質量檢測中心有限公司,北京 100088)
1 概 述
桅桿纖繩長度的計算取決于基礎至地錨的水平距離,而纖繩的水平距離又是保證桅桿各層諸方纖繩傾角不一致,就會影響纖繩內力、節點水平位移、節點剛度以及對桅身的軸向力,也就不能保證桅桿的整體穩定性。桅桿倒塌的結構上的原因主要是整體失穩,在復雜地形上,罕遇風載作用下,導致桅桿整體失穩,各方纖繩傾角不等乃是主要因素,國內曾有這樣的先例。
平坦的建筑場地,只要做到各方纖繩水平距離相等,也就滿足了要求,這是毋庸置疑的。但是實際上的天線場地,如大量的西新工程,不可能都是理想的水平面,有的場地處在山坡,抑或寬窄不一的梯田,甚至更復雜的地形,纖繩地錨的準確位置就不易確定。如果計算不確切,甚至簡化假設,就會造成如下情況:落在低處(均對桅桿中心基礎而言)的纖繩,傾角增大,內力、節點水平位移及桿身軸向力增加,而落在高處的纖繩,傾角內力、節點水平位移及桿身軸向力減少,這樣各層同一節點不同方向的受力、位移都不一致,這是不利于具有非線性特征的桅桿結構的整體空間作用的,不利于桅桿的整體穩定。
2 計算方法
對于高差較大的山坡場地,如果處在纖繩方位的坡度的斜率不變,或者近似線性關系,只要測得該方位某點與桅桿基礎的高差和相應距離,就可以得出這個方向的各層纖繩的實際水平距離。
表1即為三種纖繩傾角的實際水平距離計算公式。
一般山地場地,地形起伏變化較大,各點高差并不成線性關系,如斷坎、梯田等,用以上公式計算纖繩的水平距離就會產生誤差,尤其較高的中波桅桿,就不能采用。對這種情況,可以根據地形圖采用逐次漸進方法進行計算。
用逐次漸進方法計算纖繩水平距離的步驟(見圖1):
①以桅桿基礎底面的高程H0作為水平面,求出基礎中心至纖繩地錨處的水平距離a0;
②用比例尺在地形圖上量得a0處高程H1,得到
③由△h1算出的水平距離增量△a1;
④由a1=a0+a1,在地形圖上量得高程H2,得到△h2=H2-H1;
⑤再由△h2算出水平距離增量△a2;

桅桿纖繩水平距離計算公式 表1
⑥由a2=a1+a2,在地形圖上量得高程H3,得到△h3=H3-H2;
……
以此計算下去直至高差△hn=0,便可得到an=∑ai,即為所求的實際水平距離。
用以上逐次漸進法計算次數,一般不會超過5次便可收斂,如果采用列表方式就很簡捷。對于較高的桅桿和復雜的場地,若采用1/500地形就能得到精確的結果。
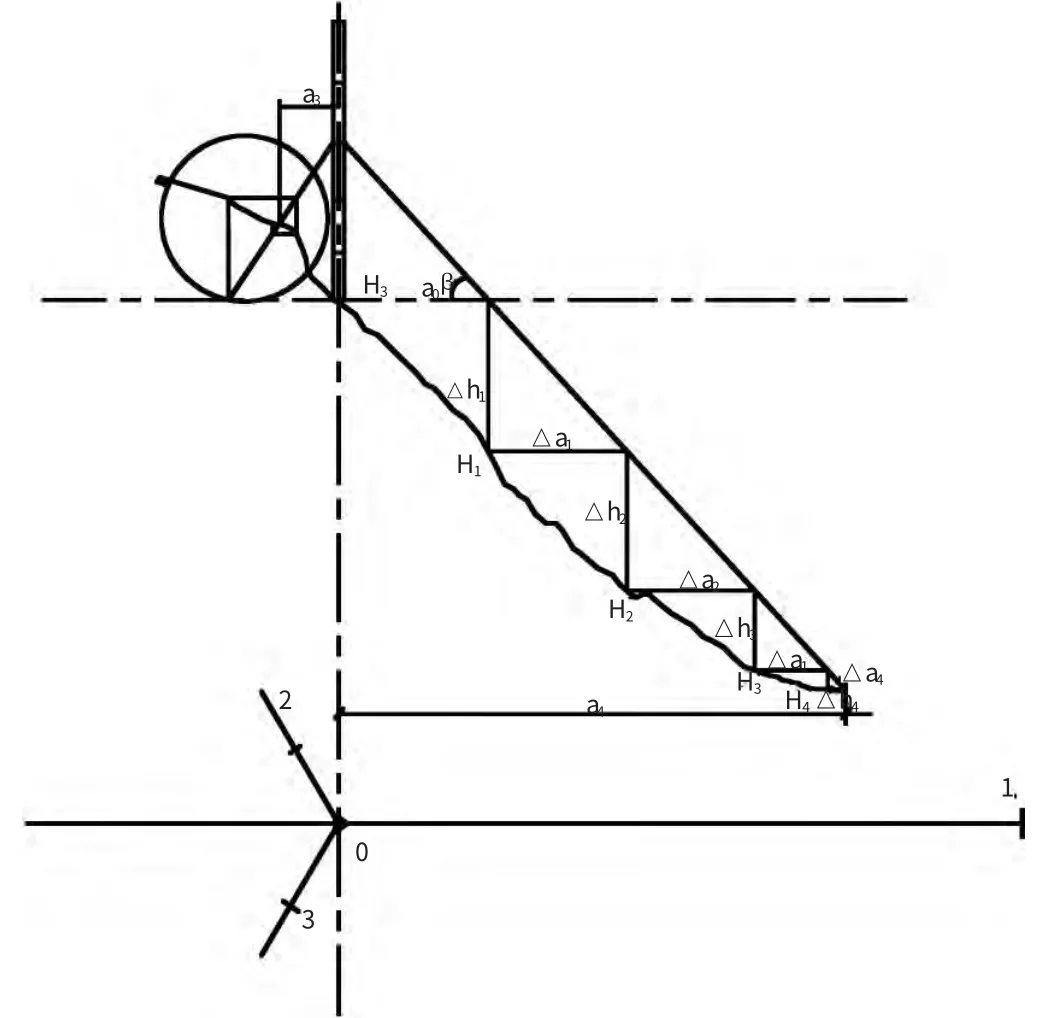
圖1 漸近法計算纖繩距離示意圖
由圖1可見,處于低坡處的纖繩水平距離呈臺階形收斂,處于高坡處的水平距離則呈縈回狀收斂,其中心點便是所求點,只是最后的水平距離為各次距離的代數和。
3 算 例
某工程天線支撐桅桿,邊寬1.5m,三方纖繩,高150m,桿身繩間跨距均為50m,基礎離地面高度為0.5m,天線場地為起伏較大的山坡。確定各方纖繩地錨矩桅桿基礎的施工定位距離和纖繩設計長度。

纖繩水平距離及長度計算 表2
用逐次漸近法計算桅桿纖繩的實際水平距離和纖繩設計長度,列表于表2(單位為m)。
例題中僅列出桅桿一個方位三層的計算數據,其余兩方從略。對于處在高坡處的水平距離按縈 形漸進法計算,此不贅列。
從例題計算結果可見,若按平地假設,則水平距離要相差67.2m~76.4m;若按a0處的高程修正一次(即為a1),水平距離也要相差23.1m~34.4m,而且都不是纖繩地錨的實際位置,最后都導致纖繩傾角增大,前者傾角為別為59.14°、60.72°、63.62°,后者分別為59.49°、53.76°、57.93°,與設計傾角45°、50°、55°比較,面目全非,有悖于地錨施工精度允許拉桿傾角-2°的要求。至于纖繩施工長度就差的更大了。嚴重的后果還在于如前所說,易使桅桿整體失穩。

