將數學建模的思想融入到經濟數學中的幾個典型案例
李輝
(南京財經大學應用數學學院,江蘇南京 210046)
將數學建模的思想融入到經濟數學中的幾個典型案例
李輝
(南京財經大學應用數學學院,江蘇南京 210046)
在經濟數學教學中怎樣將數學與經濟學聯系起來,培養財經類學生學習數學的興趣是每一位從事經濟數學教學的教師都應該關注的問題。本文我們介紹了將數學建模的思想融入到經濟數學教學中的幾個典型案例,通過這些案例教學可以將數學與經濟學有機地聯系起來,讓數學變得既生動又符合實際,取得了很好的教學效果。
經濟數學 數學建模 典型案例 教學理念
隨著現代經濟學的發展,經濟學與數學的關系越來越密切,數學語言已成為表達經濟學思想的標準的分析工具,許多經濟學模型本質上就是數學模型,同時經濟學中的某些問題也是數學的新的生長點。基于此幾乎所有的財經類高校都將數學列為重要的基礎課進行開設,這門課程稱作為經濟數學,如果要給經濟數學下個定義的話,可以這樣來描述:“經濟數學,即在經濟中應用的數學,它是經濟學與數學相互交叉的新的跨學科領域。”在財經類高校怎樣將經濟學與數學有機地聯系起來,培養學生學習數學的興趣,是每位從事經濟數學教學的教師都應該思考的問題。根據我們教學團隊多年的教學實踐和探索,我們在教學中始貫穿這樣的教學思想來講授經濟數學課程,即從經濟問題入手,講清楚經濟問題與數學之間的聯系,通過數學建模將經濟問題轉化為數學問題,再用數學方法加以解決,讓數學揭開經濟問題的奧秘。看來將經濟問題與數學聯系起來的關鍵是數學建模。下面我們介紹將數學建模的思想融入到經濟數學教學中的幾個典型案例。
1 案例一:降價能增收嗎
在市場競爭中,商品價格大戰隨處可見。例如,手機價格大戰,電視價格大戰,空調價格大戰,……。那么,降價能增收嗎?下面通過數學建模及微積分的方法來揭開其中的神秘面紗。假設商品的需求量Q只與商品的價格p有關,即需求量Q是商品的價格p的函數Q=f(p)。設價格p的改變量為△p,價格改變的百分比為△p/p,需求量Q的改變量為△Q,需求量改變的百分比為△Q/Q。現在我們要問:當價格改變1%時,需求量改變百分之多少?我們可以用量(△Q/Q)/(△p/p)來描述。

設收益為R,則R=pQ,于是
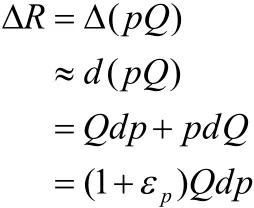
我們得到收益與價格之間關系的數學模型

根據上面的討論,我們通過數學建模及微分學的知識完全解讀上面提出的問題。
2 案例二:怎樣度量收入分配的不平等程度
隨著市場經濟的發展,許多國有企業都進行了股份制改造,一大批股份制企業的老總都成了名副其實的富翁。但我們也應該看到,近年來,我國的貧富差距確有不斷擴大的趨勢,如何反映這種貧富差距的狀況呢?下面通過數學建模和積分學的知識來分析這個問題(如圖1)。
在上載的時候,視頻資料的音頻質量要求是以監聽聲音為主,輔以上載模塊提供的軟件示波器,以UV表進行監控。特別需要注意:(1)資料內容出現差錯,或者應該是整體但內容有缺失不完整;(2)技術人員通過主觀判斷圖像或聲音質量較差的;(3)出現夾幀或彩條、黑場、靜止等不規范畫面,持續時間較長,超過5 s的;(4)出現滾動、跳閃、波紋或花屏、雜波大、馬賽克嚴重等特別明顯信號的;(5)音量大小不均或者偏大偏小,失真不清晰,有雜音噪聲干擾,明顯中斷等。在資料上載過程中,針對出現的質量問題要及時反饋給相關人員進行補救;如無法處理的,要注意看是否有必要上載該素材,或者在上載的資料中進行說明。
橫軸OH表示人口(按收入由低到高分組)的累計百分比,縱軸OM表示收入的累計百分比。當收入完全平等時,人口累計百分比等于收入累計百分比,用直線OL表示,當收入完全不平等時,用折線OHL表示。實際上,一般國家的收入分配,既不會是完全平等,也不會是完全不平等,而是在兩者之間,即曲線ODL。很顯然,曲線ODL與直線OL的偏離程度的大小,決定了該國國民收入分配不平等的程度。以橫軸OH為x軸,縱軸OM為y軸,y=f(x)表示曲線ODL,則不平等面積:
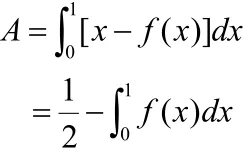
不平等面積A所占最大不平等面積(A+B)的比例
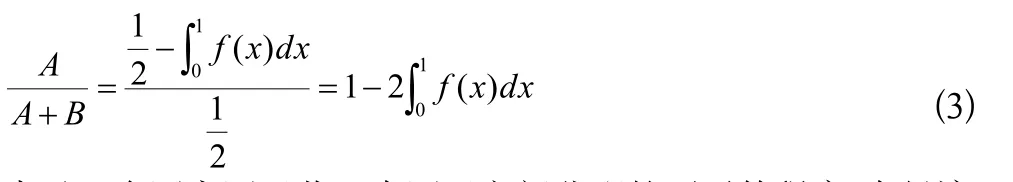
表示一個國家國民收入在國民之間分配的不平等程度,在經濟學上稱為基尼系數,記作G。

通過上面的分析,我們可以看到用定積分模型就可以度量一個國家國民收入分配的不平等程度,這是多么有意義的一件事情啊!
3 案例三:在產業集群中模塊化程度越高價值就越大嗎
隨著信息技術的發展,模塊化對于當今世界范圍內的產業結構調整和升級起著至關重要的推動作用,當今的產業已經進入到模塊化設計、生產、消費的大發展時期。模塊化的概念最早由哈佛商學院的兩位院長CarlissY.Baldwin和KimB.Clark于1997年在《哈佛商業評論》的文章中提出,兩位作者在該論文中指出,模塊化現象在幾個產業領域里從生產過程擴展到了設計過程,并且敏銳地指出了模塊化對產業結構調整所具有的革命性意義。模塊是指半自律性的子系統,通過和其他同樣的子系統按照一定的規則相互聯系而構成的更加復雜的系統或過程。根據這個概念,將一個復雜的系統或過程按照一定的聯系規則分解為可進行獨立設計的子系統的行為,我們稱之為模塊化分解。按照某種聯系規則將可進行獨立設計的子系統統一起來,構成更加復雜的系統或過程的行為,我們稱之為模塊化
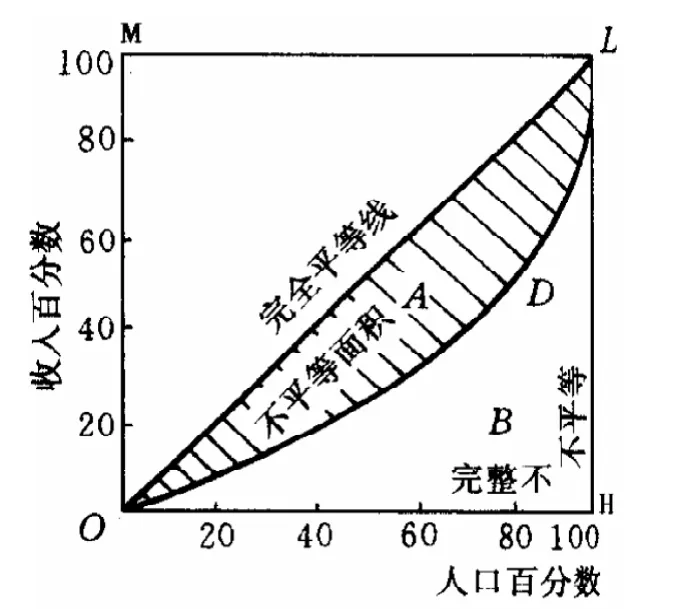
圖1
在產業集群中模塊化程度越高價值就越大嗎?下面我們用數學建模和概率論的知識來解答該問題。為了定量討論模塊化的價值,我們先作幾個假設:
(1)假設整體系統是由n個有價值的模塊組成的,這n個模塊的價值相加就是整體系統的價值。
(2)設整體系統含有N個設計參數,第j個模塊所含有的設計參數為
(3)隨著技術進步,模塊化成本不斷降低。相對于模塊化創造的價值而言,模塊化成本可以忽略。設整體系統的價值為X,它是一個隨機變量,它是由大量相互獨立的隨機因素(設計指標)的綜合影響所形成的,而其中每一個別因素在總的影響中所起的作用都是微小的,根據概率論中的中心極限定理,我們認為X服從均值為0,方差為的正態分布,即
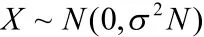
假設第j個模塊設計結果的價值為Xj,它也是一個隨機變量,假設Xj服從均值為0,方差為的正態分布,即相互獨立,于是模塊化后整個系統的價值為:
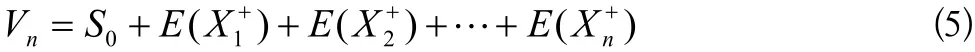
其中S0為整個系統模塊化前所具有的價值,稱為基準價值;
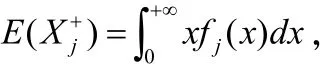
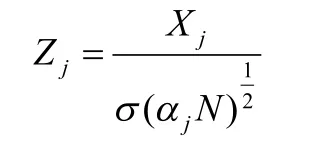
則Zj服從標準正態分布,即
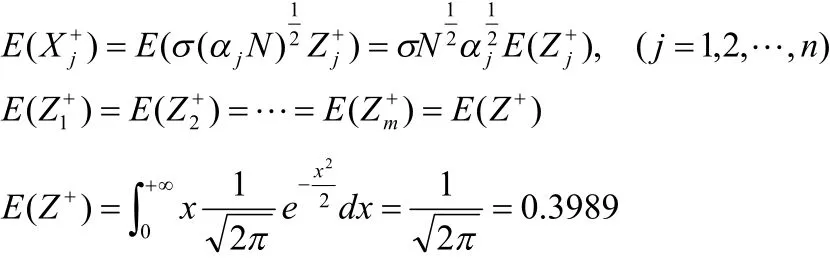
這樣(1)式就變為:
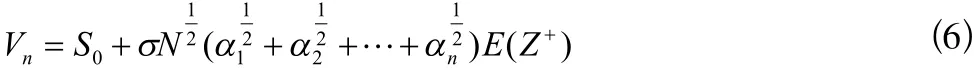

于是得到下面的結論:
在上面模型的假設下,具有N個設計參數的整體系統被分成n個分別具有設計參數的的模塊,模塊化所帶來的價值為:

因為
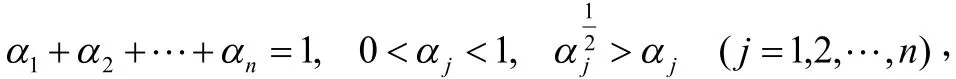
所以
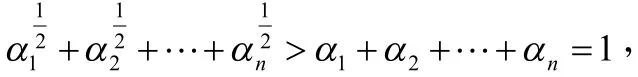
由(8)式知:

由此可得到關于模塊化價值的下面的結論:
4 結語
采用模塊化比不采用模塊化將獲得更大的價值。且隨著技術進步帶來分工的進一步深化,模塊化程度越高(模塊數越多),價值也越大。以上是我們將數學建模的思想融入到經濟數學教學中的幾個典型案例,通過這些案例教學,可以將數學與經濟學有機地聯系起來,讓數學變得既生動又貼近實際,也提高了財經類學生學習數學的積極性。今后我們會將這種教學理念始終貫穿在整個經濟數學教學的實踐中,并在教學實踐中不斷完善,為財經類院校培養出具有創新能力的有用人才。
[1]張從軍,王育全,李輝,劉玉華.微積分(第二版)[M].上海:復旦大學出版社,2009.
[2]黎詣遠.經濟數學基礎[M].北京:高等教育出版社,1998.
[3]錢書法,李輝.企業共生模式演進及其原因分析[J].經濟管理,2006,398(14):47-53.
[4]Baldwin,Carliss Y.and Kim B.Clark.Managing in an Age of Modularity[J].Harvard Business Review,1997,75(5):84~93.
[5]史樹中.諾貝爾經濟學獎與數學[M].北京:清華大學出版社,2002.
南京財經大學教改項目(JGZ1304)。集成。模塊化結構主要由三個部分構成。(1)“設計規則”。設計規則由在行業內具有核心競爭力,有品牌產品且占主導地位的企業來制定;(2)“模塊”。按設計規則將整個系統分解成若干個子系統,稱其為模塊,每個模塊必須遵守設計規則,但其具體操作可以獨立進行;(3)“系統集成與檢驗模塊”。對模塊進行檢驗,選擇符合規則的模塊并組裝成系統,并使各模塊間在整個系統中達到和諧。

