一種狀態維修適用性的定量分析方法

昝 翔 張仕新 劉艷超李 浩 韓朝帥

（1.裝甲兵工程學院技術保障工程系 北京 2.中國人民解放軍駐5460廠軍事代表室 北京）

隨著高新技術的應用，裝備的故障規律和故障模式日趨復雜化，定時維修的適用范圍逐步減小，使得狀態維修（Conditionbased Maintenance，CBM）逐步得到重視和推廣。CBM可以充分利用裝備的剩余壽命，在保證可靠性的前提下提高裝備的可用度。對于裝甲裝備實現精確保障，減少維修保障費用具有重要的意義。

對裝甲裝備所有的維修單元進行CBM是不現實的，也沒有必要，在確定CBM對象時首要進行適用性性分析。對于裝備CBM是否符合CBM的適用條件，有定性分析和定量分析兩種方法。定性分析主要是通過設定一些評價因素，對維修單元選取最優的維修方式。定量分析則通過數學方法，尋找維修單元的狀態變化是否符合CBM的適用條件。

一、狀態維修適用性

1.狀態維修基本原理

大部分故障的發生是一個逐漸變化的過程，這個過程可用圖1的P-F曲線表示。其中O點為故障萌發點，即狀態劣化的實際起點；P點為潛在故障點（Potential Failure），從這點開始異常的狀態可以通過現有的技術手段準確的檢測；F點為功能故障點（Functional Failure），即裝備最終失效的時間點。從P點到F點之間的時間長度稱為P-F間隔[1][2]。

CBM的基本原理是當P-F間隔期足夠長，在P點和F點之間能夠通過一定的手段，檢測出裝備的故障征兆，并且使用相應的維修措施，預防裝備功能故障發生。

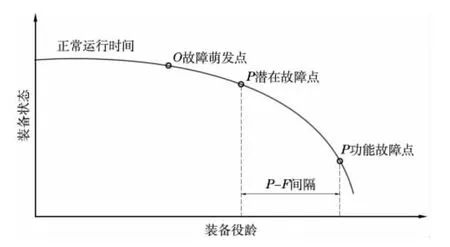
圖1 P-F間隔曲線

2.狀態維修的適用條件

根據CBM的基本原理，可以得出CBM的適用條件共有兩點，（1）必須要有可以檢測的潛在故障點。（2）必須要有足夠長的P-F間隔期。

3.狀態維修的適用性分析原則

在分析裝備各維修單元CBM適應性時，是以單元在現有條件下可以監測到的數據為準。有了以上的先決條件，CBM適用性分析時所用的數據時還應該符合3個條件。（1）必須是在現有技術條件下可以采集的數據。（2）采集數據時不能影響裝備的正常使用，也不能影響裝備的技戰術性能。（3）所選數據必須能夠長期監測，具有普遍性，即同種類的裝甲裝備均可以采集到的數據。

二、回歸分析方法簡介

回歸分析，是指在實際問題中，尋找兩個或多個變量之間的關系，并利用觀測數據擬合系統的數學模型的方法[3]。利用回歸分析方法處理數據可分兩個步驟。

1.分析數據做出散點圖

2.建立數學模型擬合回歸曲線

根據對散點圖變化趨勢的分析，判斷數學模型，建立了數學模型之后，需要對函數中的位置參數進行估計。在具體運用時，需要通過變量變換，將非線性問題轉化為線性，再利用線性回歸的求解步驟進行運算。常見的幾種曲線回歸模型線性化方法如表 1 所示[4]。

根據文獻4，可得線性回歸分析求解步驟為：

設隨機變量 和可測變量 服從線性關系

則稱Y與x服從一元線性回歸模型。

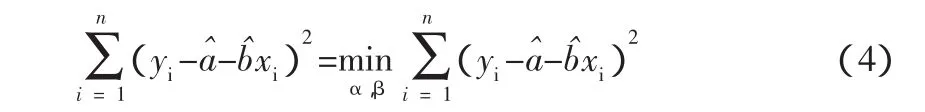
采用微分法求解，即

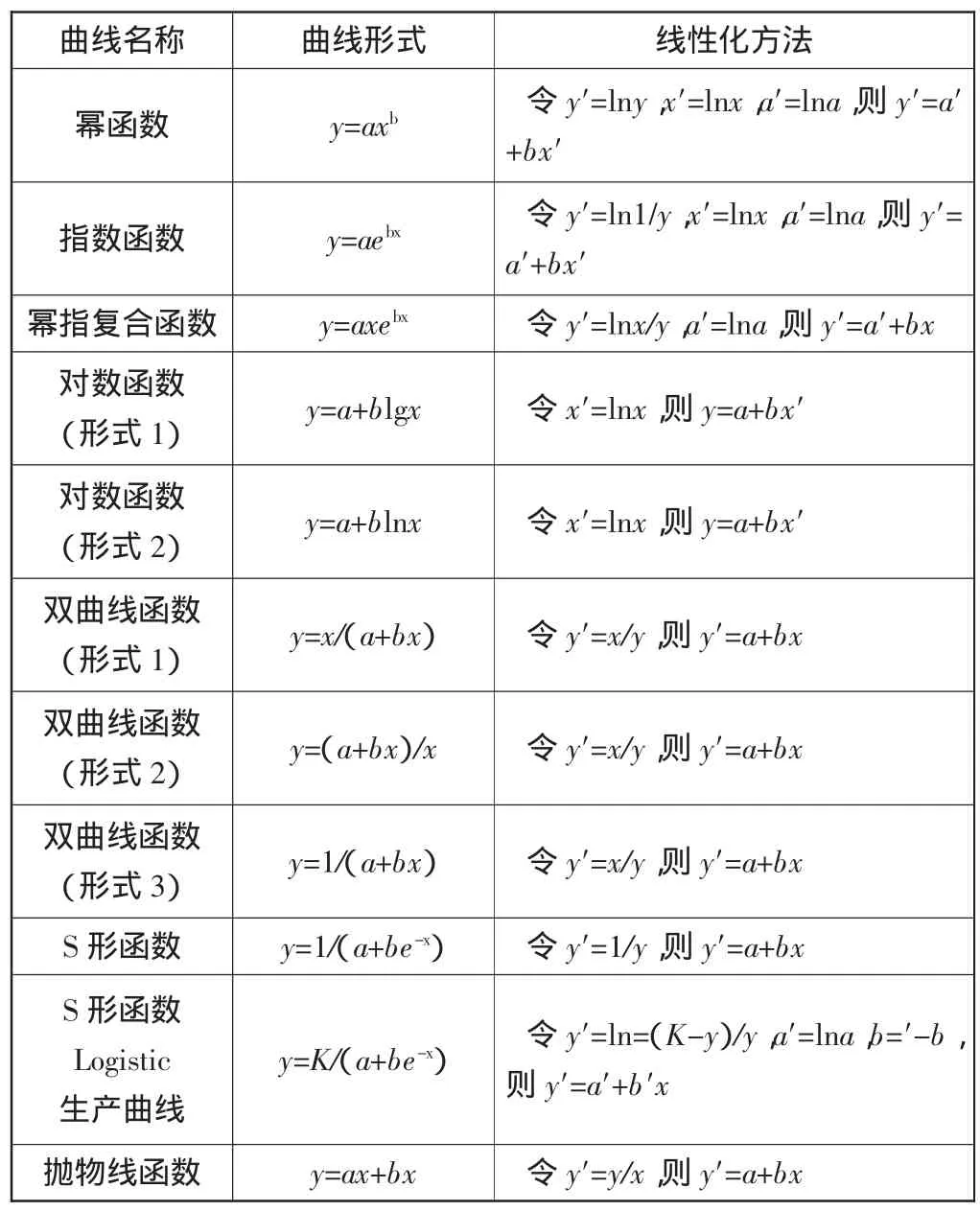
表1 常見曲線回歸模型線性化方法

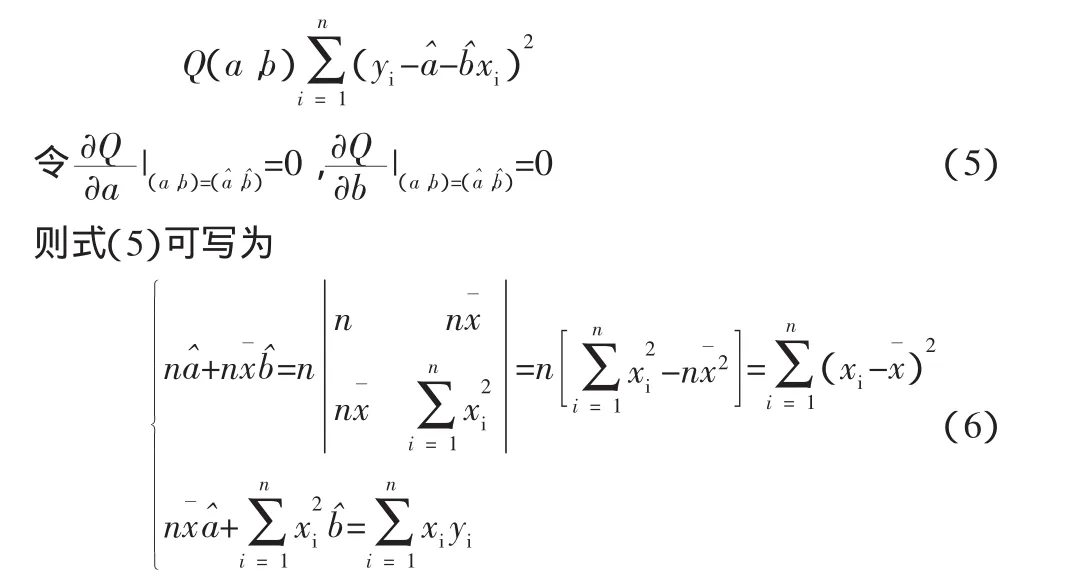
上述公式是針對一組觀測值（yi，xi）（1，2，…，n）所做的，當換為（yi，xi）時，可得（a，b）的估計量為

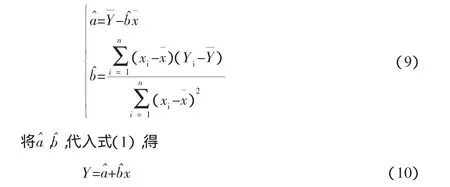
即為Y關于x的線性回歸方程。根據表1所示的線性方法，求得原函數。

3.進行檢驗，確定回歸模型

進行回歸分析求解了相關函數后，為了檢查得出的函數關系是否具有顯著性，需要對回歸模型進行檢驗，檢驗時通常使用3個指標，根據文獻3可得：

（1）可決系數R2。可決系數的定義為（11）

（2）相關系數r（13）。對統計量r和ra臨界值（查表自由度取n-m-1=n-2）進行比較，判斷顯著性水平。

（3）顯著性（F）檢驗。對統計量F和臨界值Fa（查表自由度取n-2）進行比較，判斷顯著性水平。通過顯著性檢驗，若得出擬合的函數曲線結果可以接受，則可對該函數進行下一步分析。若判斷可能符合變化規律的函數有多個，可分別進行擬合后進行比較，選取最優的擬合結果進行分析。

4.分析回歸模型得出結論

對所得的回歸模型進行分析，通過設定閾值等方法，判斷其是否符合CBM適用條件，得出適用性分析的結論。

三、實例分析

根據適用性分析原則，最終確定通過油液分析進行裝備適用性分析。根據相關規定，對裝備各維修單元的油液進行長期系統地監測，獲得大量的監測數據。對數據進行分析，找出油液的監測參數隨時間變化的規律，分析P-F曲線是否符合這一變化規律，就可以判斷該維修單元是否符合CBM適用性。

油液中各元素磨粒的含量可以反映維修單元的磨損情況和其他相關信息，因此，可以將監測元素的濃度無量綱化，然后直接作為維修單元的狀態值進行分析和研究。

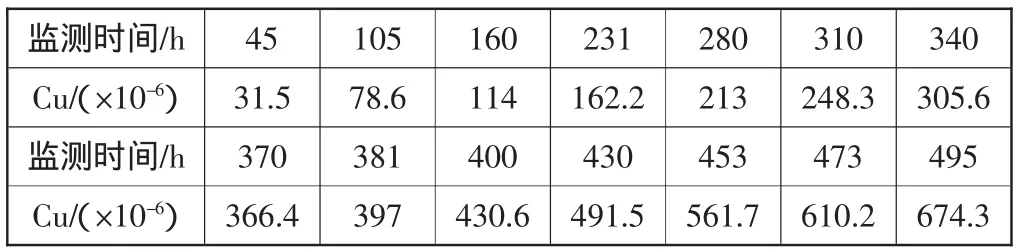
表2 Cu元素濃度變化表

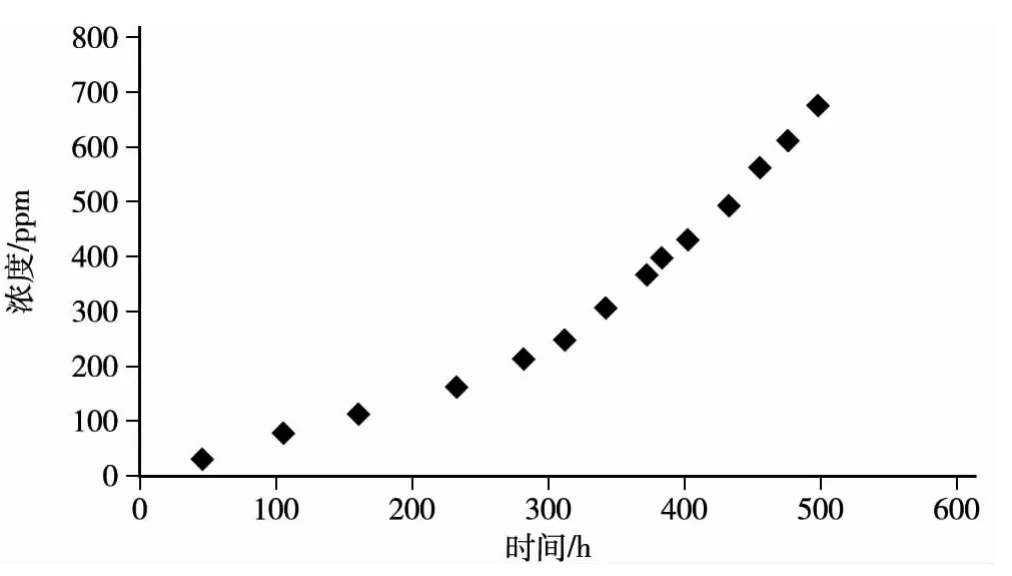
圖2 Cu元素濃度變化散點圖

以某變速箱油液數據為例進行分析，選取變速箱齒輪油中Cu元素濃度數據（表2）進行研究。

1.整理數據，繪制散點圖（圖2）

2.根據散點圖，判斷該濃度變化規律可能符合的函數模型有指數函數分布和冪函數分布

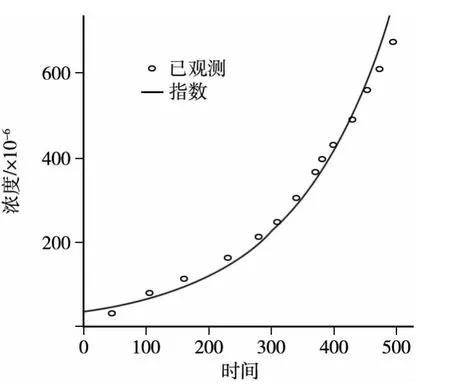
圖3 回歸分析擬合曲線圖

（1）指數函數的數學模型為（14），進行指數函數回歸分析，得到的結果如圖3所示。回歸分析結果匯總見表3。

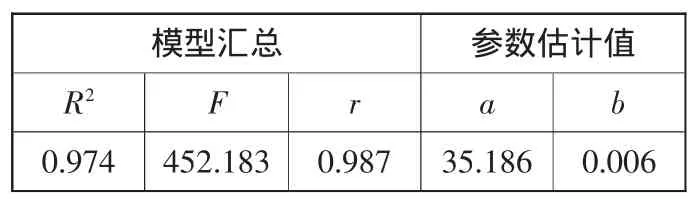
表3 回歸分析結果匯總表

（2）冪函數的數學模型為y=axb。進行冪函數回歸分析，得到的結果圖4和表4。

通過兩次回歸分析的比較，可得指數函數更符合變化規律，因此采用指數函數擬合結果進行分析。

（3）根據所得的回歸分析的結果，可判斷該變速箱狀態的變化率逐漸上升，可以設定一個斜率的閾值k，當斜率大于該閾值時，就可認為達到潛在故障的P點。因此，可以判斷該變速箱符合CBM適用條件，具有良好的適用性。

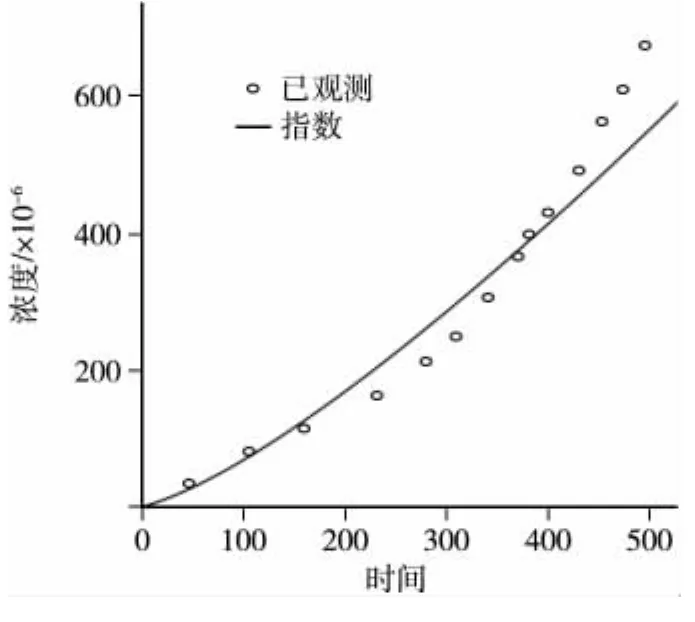
圖4 回歸分析擬合曲線圖

四、結論

通過回歸分析，定量地分析了狀態維修的適用性。減少了傳統定性分析中因主觀因素所造成的分析誤差。通過實例驗證了該方法的有效性，為CBM實施對象的確定提供了適用性分析的依據，同時為CBM的實施打下堅實基礎。

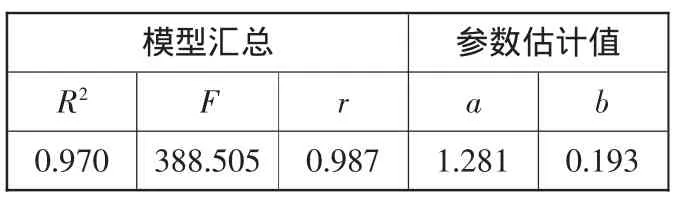
表4 回歸分析結果匯總表

1 馮廷敏，楊劍鋒，唐靜.RCM中潛在故障的凈P-F間隔評判與維修策略[J].中國設備工程，2008（8）：21-23

2 何江清，王波.軍用裝備基于狀態的維修理論研究[J].艦船電子工程，2009(12)：43-44

3 數理統計編寫組.數理統計[M].陜西：西北工業大學出版社，1999.7（1）：123

4 張建林.MATLAB&Excel定量預測與決策--運作案例精編[M].電子工業出版社.2012：86-87