定積分在經濟學中的應用

吳湘云

(麗江師范高等專科學校數學與計算機科學系,云南麗江 674100)

定積分在經濟學中的應用

吳湘云

(麗江師范高等專科學校數學與計算機科學系,云南麗江 674100)

定積分是高等數學或微積分課程的核心內容，在幾何學、物理學、經濟學中中有廣泛應用，因此成為考研數學熱點和重點內容。鑒于教科書中對定積分在幾何學、物理學中應用講解較多，本文著重舉例說明定積分在經濟學的應用。

定積分 總成本 總收益

定積分是高等數學或微積分課程的核心內容，在幾何學中有廣泛應用，如平面圖形的面積、體積、平面曲線的弧長[1]；在物理學中也有廣泛應用，如功、水壓力和引力[1]；在平均值中有重要應用，如函數平均值和均方根[1]。其實定積分在經濟學中也有廣泛應用，鑒于教科書中對定積分在幾何學、物理學中應用講解較多，本文著重舉例說明定積分在經濟學中的應用。希望對經濟類大學生的學習和備考有所幫助。

1 定積分的定義及可積的充分條件

1.1 定積分的定義

設函數 f(x)在 ［a, b ］ 上有界，在 ［a, b］ 中任意插入若干個分點把區間 ［a, b］分成 n個小區間各個小區間長度依次為在每個小區間 ［xi-1,xi］ 上任取一點作函數值 f(ξi)與小區間長度 △xi的乘積 f(ξi)△ xi，并作出和記如果不論對 ［a, b］怎樣分發，也不論在小區間 ［xi-1,xi］ 上點 ξi怎樣取法，只要當 λ→0時，和 S總趨于確定的極限 I，這時稱這個極限 I為函數 f(x)在區間［a, b］上的定積分(簡稱積分)，記作即其中 f(x)叫做被積函數， f(x)dx叫做被積表達式， x叫做積分變量， a叫做積分下限， b叫做積分上限， ［a, b］叫積分區間[1]。

1.2 函數 f(x)在區間 ［a, b］ 上可積的充分條件

定理1 設 f(x)在區間 ［a, b］上連續，則 f(x)在 ［a, b］上可積[1]。

定理2 設 f(x)在區間 ［a, b］上有界，且只有有限個間斷點，則 f(x)在 ［a, b］上可積[1]。

2 定積分的簡單經濟應用

2.1 已知某經濟變量的變化率求該變量

若已知某產品的總產量 Q的變化率是時間 t的連續函數，即則從時間 t=t0到時間 t=t1期間，該產品的總產量 Q的增加值為若已知 t=t0時的總產量為 Q0，則總產量函數

例1:設某產品在時刻 t總產量的變化率為 f( t) = 100+ 12 t -0 0.6t2(單 位/小時) 求從 t=2到 t=4這兩小時的總產量[3]。

例2:（考研數學3試題）設某產品總產量 Q的變化率為f( t) = 200 + 5t - 0.5t2,求：(1)在 2≤t≤6這段時間中該產品總產量的增加值；(2)總產量函數[2]。

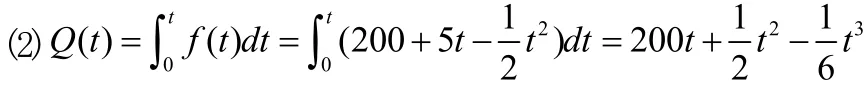
2.2 已知邊際成本求總成本

若已知生產某種產品的固定成本為 C0，邊際成本 M C=C′( x)，其中x是該產品的產量，則生產該產品的總成本函數是

例3設某種商品每天生產 x單位時固定成本為20元，邊際成本函數為 C′( x) = 0.4 x+ 2(元 /單位) ，求總成本函數 C( x)。如果這種商品規定的銷售單價為18元，且產品全部售出，求總利潤函數 L( x)，每天生產多少單位時才能獲得最大利潤[3]。

解：固定成本為20元，即 C0=20，所以每天生產 x單位時總成本函數為

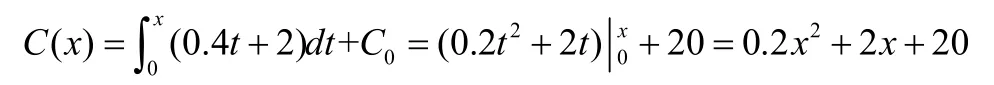
設銷售 x單位商品得到的總收益為 R( x)，根據題意有 R( x)= 18x

所以L( x) = R( x ) - C( x ) = 18 x - (0.2 x2+ 2 x + 20) =- 0.2 x2+ 16 x -20

由 L′( x) =-0 .4 x+ 16 = 0得 x=40 ，而 L′(40) =-0 .4 ＜ 0，所以每天生產40單位時才能獲最大利潤。且最大利潤為 L (40) =-0.2× 402++16× 40 -20 = 300(元 )

2.3 已知邊際效益求總收益

若已知銷售某種產品的邊際收益 M R=R′( x)，其中 x是該商品的銷售量，則銷售該商品的總收益函數是

例4已知生產某商品 x單位時，邊際收益函數為 R′( x) = 300-(元 /單 位) ，試求生產x單位時總收益 R( x)以及平均單位收益

例5設生產某產品的固定成本為50，產量為 x單位時的邊際成本函數為 C′( x) = x2- 14 x + 111，邊際收益函數為 R′( x) = 100 - 2x.求總成本函數，總收益函數和總利潤函數(考研數學3試題)[2]。

3 結語

已知某經濟變量的變化率求該變量，已知邊際成本求總成本，以及已知邊際效益求總收益等問題是定積分用于經濟方面最常見的典型問題，是經濟類考研數學的重點內容如(例2、例5)，應當引起重視，其實只需深刻理解定積分概念及可積充分條件，弄清題意，就可以順利解決此類問題。

[1]同濟大學數學教研室.高等數學上冊(第四版)[M].北京:高等教育出版社,2001：337-342, 344-349, 351-355,357-362,364-367,277-279.

[2]劉西垣,李永樂,袁蔭棠.2012年數學復習全書(考研數學三 經濟類)[M].北京:國家行政學院出版社,2011:145.

[3]趙樹嫄.經濟應用數學基礎(一)微積分(修訂本)[M].北京:高等教育出版社,2003:252-253.