基于最優平滑算法的傳遞對準性能評估技術研究
王茹
(江西省南昌市中航工業洪都集團,江西南昌 330024)
基于最優平滑算法的傳遞對準性能評估技術研究
王茹
(江西省南昌市中航工業洪都集團,江西南昌 330024)
本文對傳遞對準性能評估技術進行了介紹,并對兩種最優平滑估計算法進行了分析比較,最后提出了采用區間平滑算法實現的傳遞對準評估數學模型及評估工作流程,對于工程應用具有指導意義。
最優平滑算法 評估技術
1 傳遞對準性能評估概述
1.1 性能評估定義
動基座傳遞對準性能評估技術通過選擇高精度導航系統作為參考系統,比較子慣導系統和參考系統的相應輸出值,有效地估算、修正并檢驗子慣導建立的導航坐標系及對準誤差是否滿足具體精度要求,并提供精確的初始導航值以及理論參考依據。近年來國內外的研究表明,使用卡爾曼濾波技術是進行評估的有效方法。
1.2 性能評估要求
要建立動基座傳遞對準性能評估系統進行性能評估必須滿足以下要求:
(1)所選擇的參考系統的導航輸出精度要比子慣導的同類型輸出的精度高;(2)參考系統和子慣導的導航信息記錄后可進行事后處理,但要保證兩種導航數據同步;(3)參考系統與子慣導之間如果存在幅度較大的隨機相對運動則必須準確建立該隨機相對運動的模型。
2 最優平滑估計算法
2.1 固定區間平滑算法
固定區間最優平滑算法評估過程分兩階段完成[1]:首先,順時計算狀態Xk的Kalman濾波估計,選擇適當時間t0作為精度評估起始點,存儲t0后的有關濾波信息;濾波結束后,利用存儲信息,逆時遞推修正濾波估計結果,最終得到t0點的最優平滑值/X?kN及對應估計誤差方差陣Pk/N,對傳遞對準系統而言就是傳遞對準結束時刻的位置誤差、速度誤差和姿態失準角等參數。
對于離散線性系統如式(1)和式(2)所示:

最優平滑就是實現上述系統的線性最小方差估計,即使條件密度P[Xk|Z1,Z2,...,ZN]達到極大的Xk的值,記為:
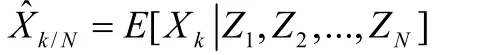
式中,k為平滑結束點,N為濾波結束點,也是平滑起始點。
固定區間最優平滑基本方程:
(1)對于k=N-1,N-2,...,1,0,固定區間最優平滑方程為:
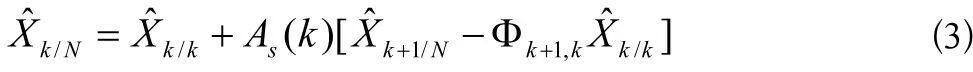
(2)固定區間最優平滑增益矩陣為:

(3)固定區間最優平滑誤差方差矩陣為:

2.2 固定點平滑算法
系統方程及觀測方程等初始條件同上。
固定點最優線性平滑的基本方程組列寫如下:
(1)對于固定的N和j=N+1,N+2,...,固定點最優平滑方程為:

或:
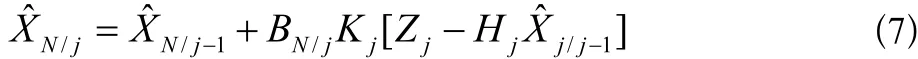
(2)固定點最優平滑增益矩陣為:


2.3 兩種平滑算法優缺點對比
對比兩種平滑算法,在固定點平滑算法中,濾波和平滑是同時進行的,都在做向前推進,而不必存儲濾波過程中的任何信息。
在固定區間平滑算法中,必須存儲濾波過程中的每一步的狀態估計、估計誤差均方差陣、一步預測均方差陣和狀態轉移矩陣信息,固定區間越長,使用的量測信息越多。但是平滑值以時刻tN的濾波值作為初值,逐步作后向遞推,在tk+1,到tk的平滑遞推過程中,使用的是tk時刻的濾波信息,平滑值依賴于估計值,若濾波已經達到比較滿意的精度,則平滑精度也可以達到比較滿意的程度。因此可以看出固定區間平滑的平滑效果比固定點平滑的效果要好。
3 性能評估方案研究
子慣導系統完成傳遞對準后進入自主導航狀態,從對準結束時刻開始記錄參考系統、子慣導系統的導航信息,兩者差值作為卡爾曼濾波器的量測輸入,利用卡爾曼濾波方程進行順序濾波并存儲相關數據,然后作逆序平滑,平滑結束后便獲得對準誤差的評估結果。
[1]弓川錦.SINS/GPS組合導航系統可觀測度分析及精度評估方法研究[D].哈爾濱工業大學,2007.
[2]韓鵬鑫,穆榮軍,崔乃剛,張軍.一種動基座傳遞對準算法性能評估的工程方法[J].中國慣性技術學報,2009,3(17):272-277.
[3]徐景碩,秦永元,顧東晴.慣導系統動基座精度評估方法[J].火力與指揮控制.2005,30(4):20~23.
[4]Yanling Hao,Zhilan Xiong,Wei Wang,et al.Rapid Transfer Alignment Based on Unscented Kalman Filter[C].Proceedings of the 2006 American Control Conference,2006:2215-2220.

