閉格的性質＊

李慶國，吳 瓊?，伍秀華

（1．湖南大學 數(shù)學與計量經(jīng)濟學院，湖南 長沙 410082；2．中南林業(yè)大學 理學院，湖南 長沙 410082）

近幾十年來，隨著理論計算機科學的發(fā)展，格理論與拓撲結構受到計算科學家和數(shù)學家越來越多的關注．在［1］中Raney通過引入完備集環(huán)的概念，給出了完備集環(huán)的格表示，也就是Raney在文［2］中定義的完全分配的代數(shù)格，并給出了完全分配完備格的等價定理．在［3］中Davey等人又給出代數(shù)格的概念，指出代數(shù)格中的任意元都是所有緊元的并，一個代數(shù)格可以構造一個與之同構的有上界的代數(shù)交結構；反之，一個有上界的代數(shù)交結構也可以構成一個代數(shù)格．在［4］中郭蘭坤和李慶國提出了F－擴張閉包空間并實現(xiàn)了代發(fā)domain 的集族表示，從而拓廣了Davey等人的結果．而且，許多學者系統(tǒng)研究了閉包系統(tǒng)的性質［5－6］．在［7］中，楊田和李慶國等對有限并是封閉的閉包算子所構建的有上界的交結構（稱之為拓撲交結構）進行研究，并引入閉格的概念，給出了拓撲交結構的格表示．在本文中，我們繼續(xù)對閉格進行研究，討論了閉格的等價刻畫和閉格與Frame的關系以及它的基本性質，并得到閉格在保任意并的滿態(tài)射下仍是閉格，最后證明了閉格運算下的像是閉格．

首先，給出閉格的一些基本概念．

定義1［3］設C為集合X上的閉包算子，若對于任意X的子集A和B均有：

C（A∪B）＝C（A）∪C（B），則C叫做拓撲閉包算子．

定義2［7］設L是X的非空子集族，若L滿足如下3個條件：

（1）對于L的任意非空子集族，都 有∩i∈IAi∈L．

（2）對于任意L中的元A和B都有A∪B∈L．

（3）X∈L．

則稱L為由上界的拓撲交結構，若L只滿足（1）和（2），則稱L為拓撲交結構．

定義3［8］設L是格，若x∈L滿足如下兩個條件，稱之為并不可約元．

（1）x≠0（當L有最小元0）．

（2）對于任意的a，b∈L，a＜x且b＜x可推出a∨b＜x．

條件（2）可以等價地寫為

（2）對于任意的a，b∈L，x＝a∨b可得到x＝a或x＝b．

我們用J（L）表示L中所有并不可約元構成的集合．

定義4［9］設L是格，若x∈L滿足如下兩個條件，稱之為并素元．

（1）x≠0（當L有最小元0）．

（2）若x≤a∨b，則對任意的a，b∈L有x≤a或x≤b．

L中的所有并素元之集記為P（L）．

定義5［7］設L是格，a∈L．設a≠1，若任意的x，y∈L，當x∧y≤a時，有x≤a或x≤b，則稱a為L的素元．

定義6［7］設L是完備格（完備下半格），對于任意的非零元a∈L， 設Da＝，若L滿足下列兩個條件，則稱L為閉格（閉半格）．

（1）對于任意的a∈L，都有a＝∨Da．

（2）對于任意的a，b∈L，都有Da∪Db＝Da∨b．

定理1［7］設C為集合X上的閉包算子，Lc是相應的有上界的交結構，則如下命題等價：

（1）C是拓撲閉包算子．

（2）若對于任意X的子集A和B均有C（A∪B）＝C（A）∪C（B）．

（3）Lc是有上界的拓撲交結構．

定理2［7］（1）若L為有上界的拓撲交結構，則L可構成閉格．

（2）若L為閉格，則是一個有上界的拓撲交結構，并且與L同構．

定理3［7］（1）若L為拓撲交結構，則L可構成一個閉半格．

（2）若L為閉半格，則是一個拓撲交結構，并且與L同構．

1 閉格的等價刻畫

在本節(jié)中，繼續(xù)對閉格進行研究，給出了閉格的等價刻畫．

定理4 設L是完備格，對于任意的a∈L都有a＝∨Da，則下列條件是等價的：

（1）對于任意的a，b∈L，都 有Da∪Db＝Da∨b．

（2）并不可約元與并素元是等價的，即J（L）＝P（L）．

（3）L是分配格．

證 （1）?（2）假設對任意的x∈P（L），存在a，b∈L使得x＝a∨b．由并素元的定義可知若x≤a∨b，則對任意的a，b∈L有x≤a或x≤b．又x＝a∨b意味著x≥a且x≥b．故x＝a或x＝b．從而P（L）?J（L）．

反之，設x∈J（L）滿足x≤a∨b．由Da∨b定義知x∈Da∨b＝Da∪Db．

根據(jù)定義6有x∈Da或x∈Db，即x≤a或x≤b．則J（L）?P（L），所以P（L）＝J（L）．

（2）?（1）Da∪Db?Da∨b顯然成立．對任意的x∈Da∨b，顯然x≤a∨b．又x∈ （ ）PL，則知x≤a或x≤b．從而x∈Da∪Db．即Da∨b?Da∪Db．因此Da∪Db＝Da∨b．

（2）?（3）對于任意的x∈J（L），設a，b，c∈L滿足x≤（a∨b）∧（a∨c），則x≤a∨b且x≤a∨c．當x≤a∨b時，由定義4知x≤a或x≤b，若x≤a，則x≤a∨（b∧c）．同理當x≤a∨c時，有x≤a或x≤c，綜合可得x≤a或x≤b∧c，從而有（a∨b）∧（a∨c）≤a∨（b∧c）．

顯然a∨（b∧c）≤a∨b，a∨c，故a∨（b∧c）≤（a∨b）∧（a∨c），所以（a∨b）∧（a∨c）＝（b∧c）∨a，即L是分配格．

（3）?（2）只需證J（L）?P（L）．

假設對任意的x∈J（L），存在a，b∈L滿足x≤a∨b，那么x＝x∧（a∨b）．因 為L是分 配格，則x＝（x∧a）∨（x∧b）．由并不可約元的定義又可知x＝x∧a或x＝x∧b，因此x≤a或x≤b，故J（L）?P（L）．所以P（L）＝J（L）．

定理5 設L是完備格，Pa＝ ｛p∈．則L為閉格當且僅當對任意的a∈L，a＝∨Pa．

證 充分性．對任意的a∈L，a＝∨Pa，而Pa?Da，則a∈L，a＝∨Da．由定理4可知只須證明L為分配格．對任意的a，b，c∈L，顯然a∧（b∨c）≥（a∧b）∨（a∧c）成立．

下面證明a∧（b∨c）≤（a∧b）∨（a∧c）．

由已知條件有a∧（b∨c）＝∨Pa∧（b∨c）．對任意的p∈Pa∧（b∨c），有p≤a∧（b∨c），則p≤a且p≤b∨c．又由于p∈P（L），因此當p≤b∨c時，可以推出p≤b或者p≤c，綜合上述可知p≤a∧b或者p≤a∧c，即p≤（a∧b）∨（a∧c），所以a∧（b∨c）＝∨Pa∧（b∨c）≤（a∧b）∨（a∧c）必要性顯然成立．

注 因此可知楊田對有上界的交結構（稱之為拓撲交結構）進行研究定義的閉格與1959年S．Papert定義的閉集格是一樣的．

由于閉格具有很好的分配性質，所以討論閉格與Locale的關系．

定義7［10］設L是完備格且滿足無限分配律，即對任意的a∈L，B?L，有a∧∨B＝∨，則稱L是Locale．

定義8［10］以滿足無限分配律的完備格為對象，以保任意并，有限交的映射為態(tài)射所構成的范疇稱為Frame范疇，并記作Frm．在Frame范疇中，對象稱為frame，態(tài)射稱為frame同態(tài)．

定義9［10］設L是Locale．若frame同態(tài)φ：L→Ω（ptL）是單射（從而是格同構），則稱LocaleL是空間式的，或稱L有足夠多的點．

引理1［10］設L是Locale，則下列條件等價：

（1）L是空間式的．

（2）對任意的a，b∈L，a＞b，存在p∈ptL使得p（a）＝1與p（b）＝0．

（3）對任意的a，b∈L，a＞b，存在L的素元x使得a＞x，b≤x．

（4）對任意的a∈L，a是L的素元之交．

命題1 空間式Locale的對偶是閉格．

證 由定理5和引理1可知空間式LocaleL的對偶滿足情形：任意的元都是L對偶的并素元之并，因而L的對偶是閉格．

2 主要性質

在本節(jié)中，給出閉格的完備子格仍是閉格的條件，證明了閉格的笛卡爾乘積仍然是閉格和閉格的保任意并的滿態(tài)射像仍是閉格．同時得到了閉格在閉包運算下的態(tài)射仍是閉格．

定義10 設L是閉格，非空子集S?L．若S對L中的任意非空并和任意非空交都封閉，即對任意的非空子集A?S，∨LA和∧LA存在時，總有∨LA，∧LA∈S成立，則稱S是L的完備子格．

引理2 設S是閉格L的完備子格且為下集，則P（L）∩S＝P（S）．

證 設x∈P（S），若存在a，b∈L使得x≤a∨b，則x≤（a∨b）∧x．由定理4知，L是分配格，則x≤（a∨b）∧x＝（a∧x）∨（b∧x）．

由S是L的下集可知，a∧x，b∧x∈S，故（a∧x）∨（b∧x）∈S．又x是S中的并素元，因此x≤a∧x或x≤b∧x．從而x≤a或x≤b，即x∈P（L）∩S，所以P（S）?P（L）∩S．反之，設x∈P（L）∩S，若存在a，b∈S使得x≤aVsb，則x≤a∨Lb，從而x≤a或x≤b，即x∈P（S）．

定理6 設S是閉格L的完備子格且為下集，則S仍是閉格．

證 由定理5只須證x＝∨s（P（S）∩↓sx）．顯然∨s（P（S）∩↓sx）≤x，設x∈S且S是L的下集，則↓sx＝↓x．而根據(jù)引理2可知

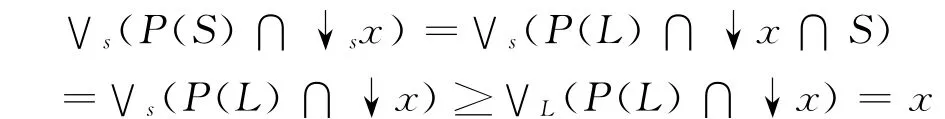
所以x＝∨s（P（S）∩↓sx），即S是閉格．

定理7 設是一族閉格，記L＝∏i∈ILi是笛卡爾乘積集，則L賦予逐點序也是閉格．

證 設（Li）i∈I為一族閉格，記L＝∏i∈ILi．由閉格的定義可知i∈I，Li為分配格．令a，b，c∈L，則有

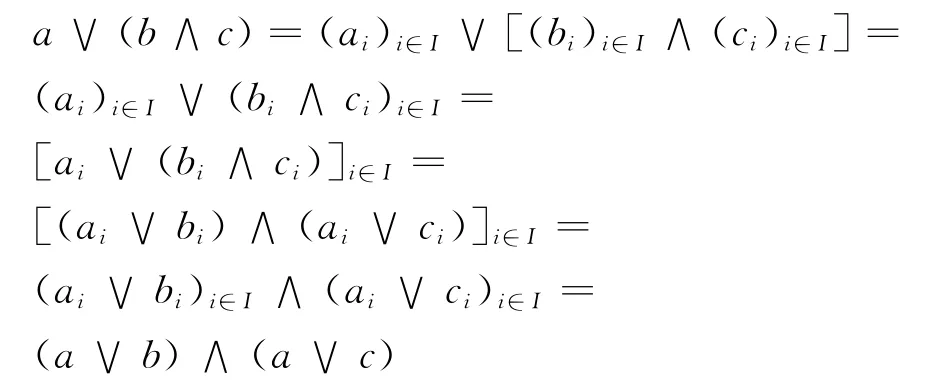
即L是分配格．對于任意的，令δi＝｛x∈且xi∈J（Li），j≠i時xj＝0｝顯然∪i∈Iδi中的元是∏i∈ILi中的并不可約元，且∪i∈Iδi在∏i∈ILi的并是（ai）i∈I．綜上可得L是閉格．

定理8 設L是閉格，Q是完備格．若f：L→Q為保任意并的滿映射，且f（P（L））?P（Q），則Q是閉格．

證 由于f為滿映射，則對任意的y∈Q，存在x∈L，使得f（x）＝y(tǒng)．

顯然∨（P（Q）∩↓f（x））≤f（x）．又L是閉格， 則f（x） ＝f［ ∨（P（L）∩↓x）］＝∨ff（P（（L））∩↓x） ．

對于任意的z∈P（L） ∩↓x，則z≤x，由于f是保任意并的映射，則f（z）≤f（x）．由f（P（L））?P（Q），則f（z）∈P（Q）．從而f（z）∈P（Q）∩↓f（x），即f（P（Q）∩↓x）?P（Q）∩↓f（x），

故f（x）≤∨（P（Q）∩↓f（x）），

所以f（x）＝∨（P（Q）∩↓f（x）），

即Q是閉格．

定義11［3］設P為偏序集，映射c：P→P稱為P上的閉包運算，若對于P中的任意元x，y都有：

（1）x≤c（x）．

（2）x≤y?c（x）≤c（y）．

（3）c（c（x））＝c（x）．

若c（x）＝x，則元素x∈P稱為閉元，P上的所有閉元組成的集合記為Pc．

引理3［3］設P是完備格，c是P上的閉包算子，則Pc是完備格且對任意的子集S?Pc，有∧PcS＝∧pS和∨PcS＝c（∨pS）．

定理9 設L是閉格，c：L→L是閉包算子，且對任意的a，b∈L，有c（a∨Lb）＝c（a）∨Lc（b），則c（L）是閉格．

證 定義c1：L→c（L），其中c1（x）＝c（x），顯然c1是單調的滿射，現(xiàn)證c1保任意并．令ai（i∈I）是L的一組元，由引理3可知c（L）＝c1（L）為完備格，則c（L）中 ∨i∈Ic（ai）存在，易知c（∨ai）≥∨i∈Ic（ai）成立．又因為c是閉包算子，則∨i∈Ic（ai）≥∨i∈Iai，從而c（∨i∈Ic（ai））＝∨i∈Ic（ai）≥c（∨i∈Iai），

故c1（∨ai）＝c（∨ai）＝∨i∈Ic1（ai）＝∨i∈Ic（ai），由定理8可知只需證c（P（L））?P（c（L））．對任意的x∈P（L），若存在a，b∈c（L）滿足c（x）≤a∨c（L）b，則a∨c（L）b＝c（a∨Lb）＝c（a）∨Lc（b）＝a∨Lb所以x≤c（x）≤a∨Lb．由并素元的定義可知，x≤a或x≤b，因此c（x）≤c（a）＝a或c（x）≤c（b）＝b，所以c（P（L））?P（c（L））得證，故c（L）為閉格．

［1］RANEY G N．Completely distributive complete lattice［J］．Proc Amer Math Soc，1952，3：677－680．

［2］RANEY G N．A subdirect－union representation for completely distributive complete lattice［J］．Proc Amer Math Soc，1953，4：518－522．

［3］DAVEY B A，PRIESTLEY H A．Introduction to lattice and order［M］．Cambridge：Cambridge University Press，2002．

［4］GUO Lan－kun，LI Qing－guo．The categorical equivalence between algebraic domains and F－augmented closure spaces［J］．Order，Doi：10．1007／s11083－014－9318－8．

［5］GUO Lan－kun，ZHANG Guo－qiang，LI Qing－guo．Fuzzy closure systems on L－ordered sets［J］．Mathematical Logic Quarterly，2011，57（3）：281－291．

［6］ERNE M C，MYNARD F，PEARL E，etal．Beyond topology，contemporary mathematics［J］．American Mathematical Society，Providence，2009．

［7］楊田，李慶國．閉格與拓撲交結構［J］．湖南大學學報：自然科學版，2007，34（3）：250－258．

YANG Tian，LI Qing－guo．On closed lattice and topological intersection structure［J］．Journal of Hunan University：Natural Sciences，2007，34（3）：250－258．（In Chinese）

［8］BIRKHOFF G．Lattice theory［M］．Revised Ed．Amer Math Soc Colloquium Publication，1948，25．

［9］GIERZ G，HOFAMANN K H，KEIMEL K，etal．Continuous lattice and domains［M］．Cambridge：Cambridge University Press，2003．

［10］鄭崇友，樊磊，崔宏斌．Frame與連續(xù)格［M］．北京：首都師范大學出版社，2000：44－106．

ZHENG Chong－you，F(xiàn)AN Lei，CUI Hong－bin．Frame and continuous lattice［M］．Beijing：Capital Normal University Press，2000：44－106．（In Chinese）