退化線性橢圓方程非常弱解的存在唯一性＊

晏華輝，顧廣澤

（湖南大學(xué) 數(shù)學(xué)與計量經(jīng)濟學(xué)院，湖南 長沙 410082）

Quittner 與Reichel在［1］中研究了帶非線性Neumann邊界條件的問題：

Ω ∈RN有界．定義了一類非常弱解的概念，并且證明了只要函數(shù)f滿足增長條件：

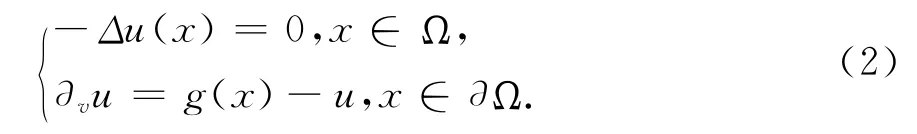
他們需要得到上面問題非常弱解的存在唯一性結(jié)果．

性質(zhì)1 令g∈L1（?Ω）．則問題（2）存在唯一弱解u∈L1（Ω）×L1（?Ω），且存在常數(shù)C＞0，使得：

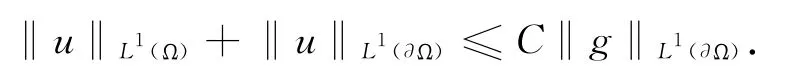
而且，若g在?Ω 上g≥0幾乎處處成立，則解u在Ω 內(nèi)與?Ω 上均幾乎處處成立u≥0．

1 預(yù)備知識和幾個引理

自然想到將上面橢圓方程非常弱解的問題推廣到退化橢圓方程非常弱解的問題．為此，我們需要在如下一類特別的區(qū)域內(nèi)考慮問題．

定義1 令H＝｛（x′，xN）：xN＞0｝為上半空間．H中的一個有界光滑區(qū)域Ω 稱為具有一片平的邊界的區(qū)域，若它滿足：

（ⅰ）?Ω＝Σ1∪Σ2，Σ1??H，且0∈int（Σ1）；

（ⅱ）int（Σi）＝Σi（i＝1，2），且int（Σ1）∩int（Σ2）＝φ．

我們將研究在一片平的邊界Σ1的區(qū)域Ω 內(nèi)的如下退化橢圓問題：

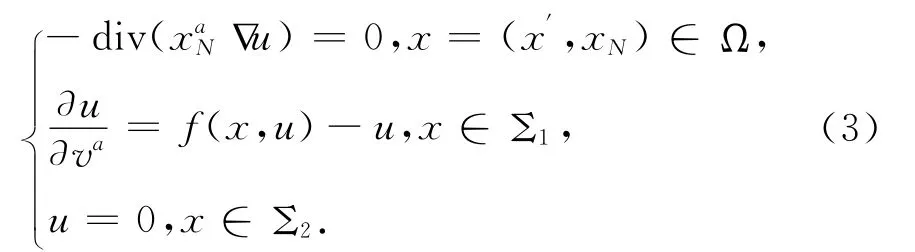
其中參數(shù)a∈（－1，1），

注 當(dāng)a＝0 時，退化橢圓問題（3）即為問題（1）．

要研究問題（3），也需要研究它對應(yīng)的線性邊界條件的問題非常弱解的存在唯一性：

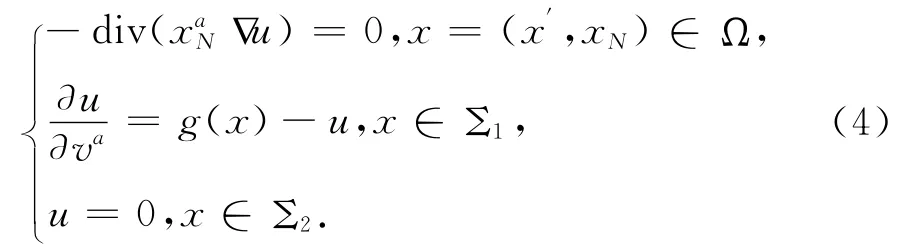
類似［1］，定義問題（4）的非常弱解的概念．

定義2 令g∈L1（Σ1），函數(shù)u∈L1（Ω）稱為問題（4）的一個非常弱解，若它滿足：

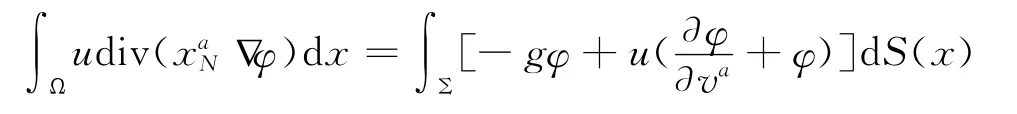
首先用變分方法得到：當(dāng)g∈L∞（Ω1）時，問題（4）非常弱解的存在唯一性．需要用到如下的退化橢圓算子對應(yīng)的極值原理．

引理1［8］若u弱滿足

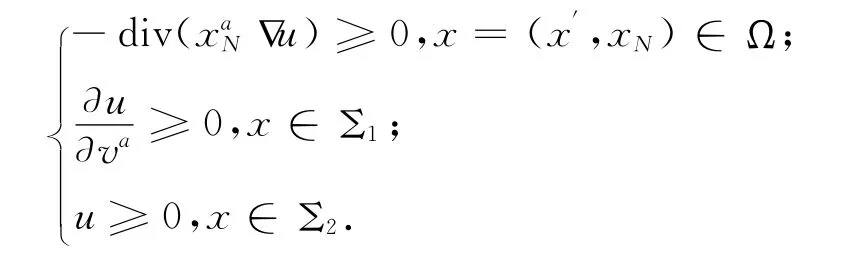
則在Ω 中u≥0．

引理2 令g∈L∞（Σ1），則問題（4）存在唯一弱解

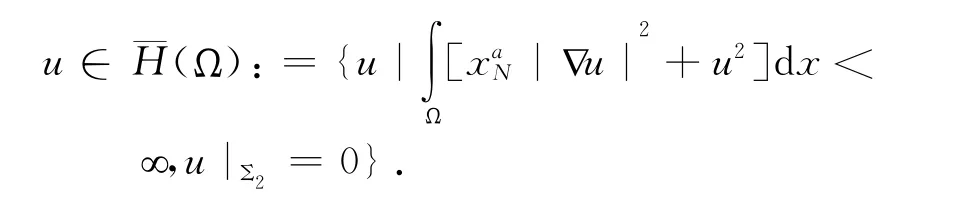
證 問題（4）對應(yīng)的能量泛函為

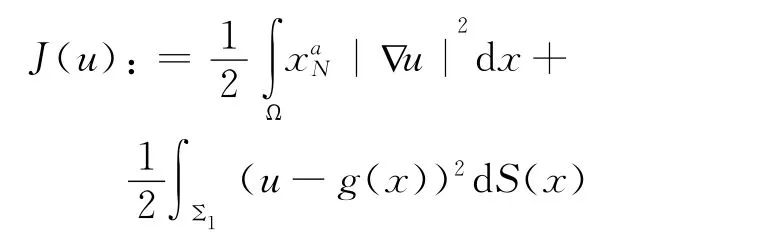
顯然，能量泛函J存在極小化子序列u｛k｝ 使得

易得

由Poincare不等式與已知條件g∈L∞（Σ1）知

其中C與k無關(guān)．

從而存在一個子列，仍記作使得：

uk→u在ˉH（Ω）的意義下，由范數(shù)的弱下半連續(xù)性及（Ω）空間的弱閉性質(zhì)知

從而u即為問題（4）的弱解．

再證唯一性．設(shè)有兩個解u1，u2，則它們的差w：＝u1－u2滿足：

由引理1可得w≡0，所以u1≡u2．

證畢．

2 主要結(jié)果

本文的主要結(jié)果如下：

定理 令g∈L1（Σ1），則問題（4）有唯一非常弱解u∈L1（Ω），且存在C＞0，使得

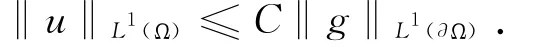
而且若在?Ω上g≥0幾乎處處成立的話，則在Ω 內(nèi)幾乎處處成立u≥0．

證 先證明存在性．由分解g＝g＋－g－，其中g(shù)＋＝max｛g（x），0｝，g－＝－min｛g（x），0｝．只需對函數(shù)g≥0的情形證明非常弱解的存在性即可．

令gk（x）＝min｛g（x），k｝，k∈N．則

gk→g在L1（Σ1）意義下，當(dāng)k→∞，

令uk∈ˉH（Ω）為如下問題的弱解

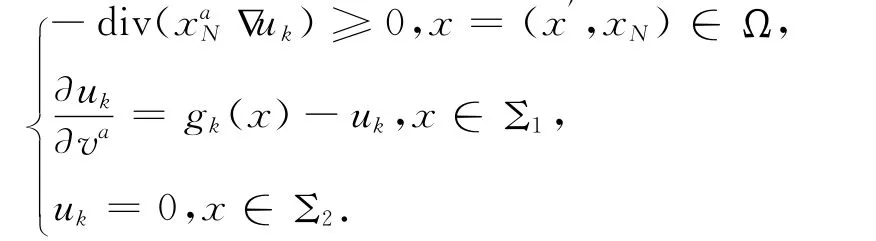
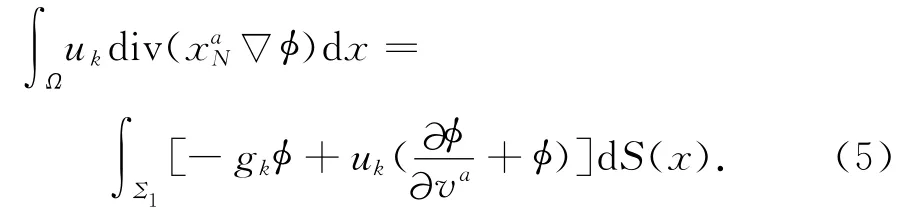
由（5）式可得

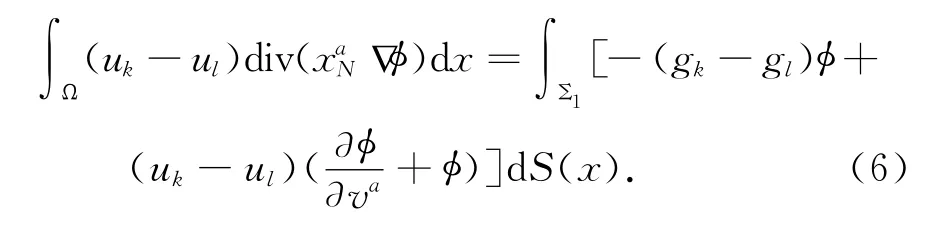
由引理2可知，如下問題存在古典解ψ

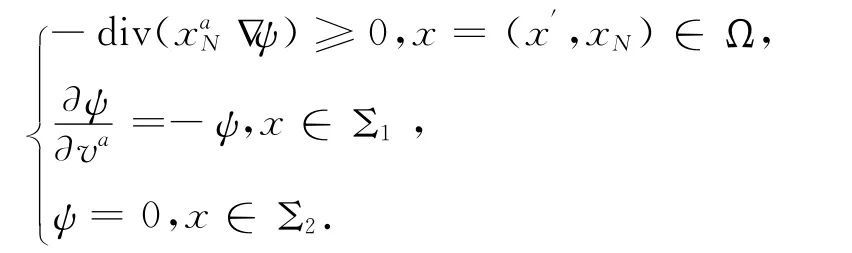
將（6）中的實驗函數(shù)取上面問題的解ψ，則有

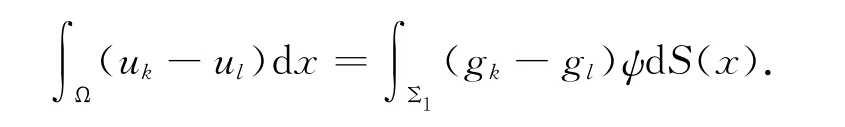
由引理1知，在Ω中ψ≥0及uk－ul≥0，當(dāng)k＞l．所以｛uk｝為L1（Ω）中的一個基本列．從而在L1（Ω）中uk→u．在（5）式中，取極限，令k→∞，得到結(jié)論：u為原問題（4）的非常弱解．存在性得證．

唯一性的證明同前面引理2，略去．

證畢．

推論 方程組

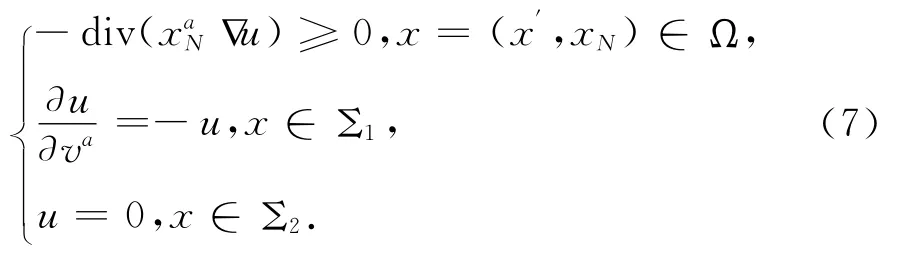
只有零解．

證 顯然u≡0是方程組（7）的解，由定理可知方程組（7）的解唯一，故方程組（7）只有零解．

證畢．

［1］QUITTNER P，REICHEL W．Very weak solutions to elliptic equations with nonlinear Neumann boundary conditions［J］．Calc Var Partial Diff Equ，2008，32（4）：429－452．

［2］BIDAUT－VERON M F，PONCE A，VERON L．Boundary singularities of positive solutions of some nonlinear elliptic equations［J］．C R Acad Sci Paris Ser I Math，2007，344（2）：83－88．

［3］HU B．Nonexistence of a positive solution of the Laplace equation with a nonlinear boundary condition［J］．Differential Integral Equations．1994，7（2）：301－313．

［4］MCKENNA P J，REICHEL W．A priori bounds for semilinear equations and a new class of critical exponents for Lipschitz domains［J］．J Funct Anal，2007，244（1）：220－246．

［5］PACARD F．Existence de solutions faibles positive de dans des ouverts bornes de［J］．C R Acad Sci Paris Ser．I Math，1992，315（7）：793－798．

［6］PACARD F．Existence and convergence of positive weak solutions of in a bounded domains of［J］．Calc Var Partial Diff Equ，1993，1（3）：243－265．

［7］QUITTNER P，SOUPLET PH．A priori estimates and existence for elliptic systems via bootstrap in a weighted Lebesgue spaces［J］．Arch Ration Mech Anal，2004，174（1）：49－81．

［8］CABRE X，SIRE Y．Nonlinear equations for fractional Laplacians I：regularity，maximum principles，and Hamiltonian estimates［J］．Ann Inst H Poincar’｛e｝Anal NonLin’｛e｝aire，2014，31（1）：23－53．