2014年江蘇省鹽城市數學中考試題類型及解題思路研究

張玉祥

摘 要： 初中數學畢業考試是義務教育階段的最后一次檢測性的考試，雖然不如高考那般可以直接決定一個人的命運，但是在學生生涯中也是十分重要的，它關乎學生升學。對于初中生來說，這也是一次非常重要的考試。本文針對2014年江蘇鹽城的數學中考試卷進行了詳細試題類型及考試思路的分析，希望對中考學子有幫助。

關鍵詞： 數學中考試題 試題類型 解題思路

隨著新課改在我國的逐漸推行，我國初中教學有了一定的改善，在中考的考試試題中就有所表現。江蘇省作為我國的一個中考大省，是我國新課程標準改革的前沿，面對新課改的要求，2014年江蘇省鹽城市的數學中考在一些方面也進行了一些改革，取得了一定成效。本文著重研究了2014年江蘇省鹽城市的中考數學試題，希望對江蘇省乃至全國的中考學子的考試有所幫助。

一、2014年江蘇省鹽城市數學中考試題類型

1.試題綜述

總體來說，2014年江蘇省鹽城市的數學中考試題具有綜合性、實用性及基礎性的特點，試題難度適中，主要注重考查學生的綜合能力，尤其是對于知識的靈活運用能力，體現了新課改的一些理念。

2.試題結構

2014年江蘇省鹽城市的數學中考試題包括三部分內容。第一部分是填空題，共有8小題，滿分24分；第二部分是填空題，共有10小題，滿分30分；第三部分是解答題，共有10小題，滿分是96分。這樣就對數學中考試題的整體結構進行了解析，希望有助于江蘇省的中考學子“知己知彼”，做好數學中考的心理準備[1]。

3.試題類型

2014年江蘇省鹽城市的中考試題依然沿襲傳統，題目涉及的面比較廣，但是考查的內容以基礎性知識為主，同時試題具有梯度性，整個試題遵循由易到難、由淺入深的規律。另外，整套試卷涉及的數學內容比較多，范圍比較廣，既有函數又有幾何。

例如，填空題中1、2、4、5、6題是函數題，剩下的幾道題是幾何題，一般來說填空題的前面幾道題比較的基礎，后面的幾道題有著一定的難度，尤其是最后一道題，對于一般學生來說有一定的難度，需要學生具有堅實的基礎，靈活的思維才可以做出。2014年江蘇省鹽城市的數學中考試題的最后一個填空題考查的是一個重要的知識點——“反比例函數”。一般來說，反比例函數對于初中生來說有一定的難度，學生總是將反比例函數與函數混淆，另外在這道題中，將反比例函數與圖形進行結合更增加了一定的難度。

二、2014年江蘇省鹽城市數學中考試題的解題思路

1.選擇題

選擇題在數學試卷中占據了30分的分量，總體來說分值還是比較高的，但是較填空題及解答題來說，選擇題是較容易做的一種題型。選擇題給了四個選項，因此在做選擇題的時候，做完選擇題之后，要觀察四個選項，根據選項檢查自己做得是否正確，是否有落下的條件；我們做選擇題時，遇到實在不會的題目，例如選擇題的最后一題，可以憑借做題的經驗，選擇一個最有可能的答案，這樣也有25%做對的可能[2]。

例如，2014年江蘇省鹽城市數學中考選擇試題中的第6題，求不等式組的解集。在得出答案后，一定要根據選項進行檢查，是否有條件沒考慮到，當我們得出答案是A選項的時候，就要根據C選項考慮是否出現了差錯，這樣有助于提高做題的正確率。

2.填空題

填空題在整套試卷中占了30分，填空題較之選擇題有一定的難度，但是填空題一般是考查學生的基礎知識及綜合能力。填空題作為小題，不要求解題過程，因此雖然有一定的難度，但是只要細心、仔細，基礎知識足夠牢靠，填空題就比較容易對付的。

例如，2014年江蘇省鹽城市數學中考試題填空題的第10題，是求取值范圍，在做題的時候學生往往只是直接得出結論，忽視了題目本身的限制條件。由此可知，填空題主要考查學生的綜合能力及基礎知識，因此填空題的應對方法便是細心、認真、仔細。

3.解答題

解答題一般是學生最頭疼的題目卻也是占據分值最高的題目。中考的解答題呈現出綜合性的特點。因此，在解答題中一般都會對課本的主要知識點進行考查，涉及的范圍比較廣，內容比較復雜[3]。

例如，2014年江蘇省鹽城市數學中考試題，在解答題中不僅涉及了一次函數、不等式、幾何證明，還涉及了概率等課本的主要知識點。可見對于學生的綜合能力的考查十分注重。

解答題對于學生的要求更嚴格，不僅需要學生細心，還需要學生思維邏輯清晰。簡答題要求學生將解題思路寫下來，這樣就對學生做題的思路有了清晰的要求。在做簡答題的時候，學生不僅僅要得出結論，過程也是十分重要的。

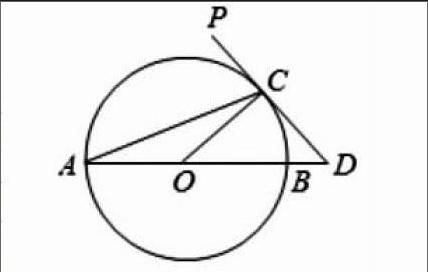
例如，江蘇省2014年鹽城市數學中考試題的24題。如圖，AB為⊙O的直徑，PD切⊙O于點C，交AB的延長線于點D，且∠D=2∠CAD.

（1）求∠D的度數；

（2）若CD=2，求BD的長.

不僅要求我們求得結果， 更要求我們注重過程，在求解過程中思路要清晰，對于邏輯思維能力的要求非常高，因此對于解答題的解題思路是，不僅要細心，注重審題，而且要對基礎知識牢固掌握，并能夠靈活運用，將知識綜合起來。

結語

從2014年江蘇省鹽城的數學中考試題中我們可以看出試題更注重學生對于基礎知識的掌握及靈活運用，同時注重學生綜合能力的考查。分析中考試題讓我們知己知彼，在中考中掌握主動權，探究解題思路讓我們在解題中少走彎路，提高解題效率，從而有助于提高成績。

參考文獻：

[1]喻平.數學問題解決認知模式及教學理論研究[D].南京師范大學，2010，（09）：10-11.

[2]李善良.現代認知壓觀下的數學概念學習與教學理論研究[D].南京師范大學，2010，（11）：14-15.

[3]曹一鳴.數學教學模式的重構與超越[D].南京師范大學，2011，（03）：15-16.endprint