數字分析法在消防統計中的應用
●趙步逵,劉東海
(武警學院 a.研究生隊;b.消防指揮系,河北 廊坊 065000)
隨著社會經濟快速發展,我國每年由火災所造成的財產損失和人員傷亡情況逐漸引起了社會各界的廣泛關注。以火災統計四項指標為主的消防統計數據質量的好壞直接影響著我國火災安全形勢的分析和未來公共消防政策的制定。同時,隨著《中華人民共和國統計法》的修訂實施和政府績效評價的推廣完善,消防統計數據的質量也不斷受到社會各界的關注。數字分析法是以Benford定律為基礎發展起來的一種根據數字分布規律來檢測異常的方法,它具有操作簡單,無需專業知識背景即可完成檢測任務的優點。本文擬利用我國2011年消防統計數據進行實證分析,對如何運用數字分析法來檢驗我國消防統計數據質量做出一些探討。
1 Benford定律的原理
Benford定律被稱為“第一位數分布規律”,該定律揭示了海量數據中第一位數字出現的頻率。通過對Benford定律中數字分布規律的應用研究,人們可以將Benford定律作為對統計數據進行質量檢驗的理論依據。在過去半個多世紀里,國內外學術界有關Benford定律的應用研究大部分都集中在財產審計和金融經濟領域,在消防統計領域中關于Benford定律的應用研究還處于空白階段。
2 Benford定律的應用
Benford定律要求被檢測數據的第一位數字應該為有效數字,所以在進行實證檢驗時首先運用測試工具對所有需要檢驗的數字進行提取和整理,保證第一位數字符合非零、非負的原則然后對各個數字出現的頻率進行計算分析。
2.1 測試工具
應用Benford定律在進行數據質量檢驗時可以借助計算機實現快速檢驗分析,通常各類統計分析軟件,如Excel、SPSS、SAS都滿足檢驗所需要的功能要求。考慮到Benford定律進行數據檢驗時需要提取各個數據的第一位數字,而Excel軟件對這項操作更為簡便易行,所以本文擬使用微軟辦公軟件的Microsoft Office Excel的2003版作為數據處理軟件。
2.2 測試方法
2.2.1 輸入樣本數據。將樣本數據全部導入或者拷貝到Excel電子表格的第A列,假定共有1 000個數據。
2.2.2 整理樣本數據。將數據拷入第B列,在B列中首先選擇菜單中“升序排列”,將數據按照從小到大依次排列。通過觀察,如果數據中有小于1的數據(如0.55)。可以直接在第B列第一行輸入公式[B1*10]或[B1*100]。通過下拉菜單拷貝公式至數據最后一行,對整個數據樣本乘以10或100(該項操作符合數據集比例不變性,篇幅所限不做贅述)。
2.2.3 截取樣本數據的首位數。在第C列的第一行,設置函數[LEFT(B1,1)]并下拉拷貝公式至數據最后一行,電腦自動將第B列的首位數選出并存儲顯示在第C列。
2.2.4 計算首位數(1~9)的出現頻數。在第D列的第n行輸入公式:[COUNTIF(Cn:C1000,n)];電腦就會自動在第D列出現樣本首位數字1~9的出現頻數。
2.2.5 計算首位數(1~9)出現的頻率。在第E列第一行輸入公式[D1/1000],下拉拷貝公式到第9行,在第E列中就會依次出現首位數(1~9)出現的頻率。
2.2.6 與Benford定律分布的比較。在第F列的前9行中輸入Benford定律的期望分布概率,在第G列的第一行中輸入公式[=E-F],求得所檢驗的數據分布和Benford定律分布的差異值。
2.2.7 進行檢驗。通過 Excel軟件的統計函數Pearson函數可以計算出相關系數的數值。
3 實證分析
3.1 數據來源
本文以公安部消防局編制的《中國消防年鑒》(2012)[1]中 2011年我國 31個省、自治區、直轄市(不包含新疆生產建設兵團)的火災起數、火災直接損失(萬元)和火災燒毀建筑(m2)這三類重點統計數據為實證分析的樣本。消防統計數據中沒有最大值和最小值的限制,也不存在人為賦值的影響,符合Benford定律的檢驗要求。為保證分析過程的準確性,對以上樣本數據進行整理,剔除含0的數據4條,共得到有效數據1 415個,基本可以滿足Benford定律對數據集規模的要求。
3.2 第一位數字
將樣本數據按照火災起數、火災直接損失(萬元)和火災燒毀建筑(m2)劃分成三項統計數據。其中火災起數包含473個數據,火災直接損失(萬元)包含471個數據,火災燒毀建筑(m2)包含471個數據。運用Excel軟件求出上述三項統計數據中第一位數字的個數和頻率(精確到0.000 01),然后將各項統計數據的數字頻率與Benford定律中第一位數字分布的頻率在一起進行觀察比較,如圖1所示。可以看出,火災起數,火災直接損失(萬元)和火災燒毀建筑(m2)三項統計數據的第一位數字頻率分布基本與Benford定律的第一位數字頻率分布相一致,所存在的差別是否顯著還需要進行進一步檢驗分析。
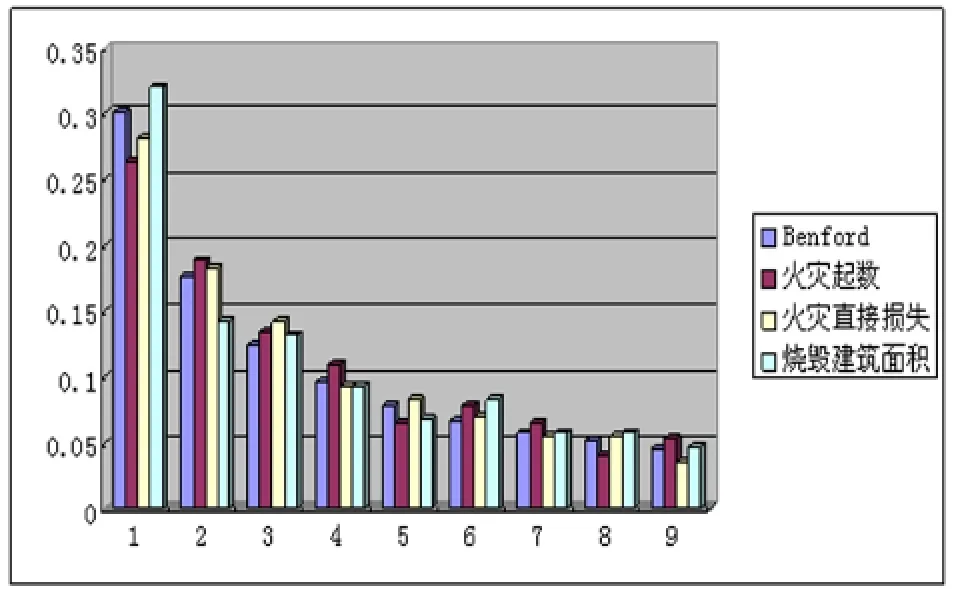
圖1 三項統計數據與Benford定律的頻率分布3.3 檢驗分析
本文采用Pearson相關系數進行檢驗分析,Pearson相關系數是用來反映兩個變量線性相關程度的統計量,公式如下:
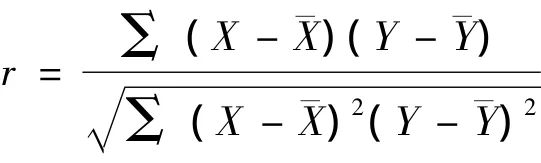
式中,r表示相關系數,描述的是兩個變量間線性相關強弱的程度。r的取值在 -1與+1之間,絕對值越大表明相關性越強。若r﹥0,表明兩個變量是正相關;若r﹤0,表明兩個變量是負相關;若r=0,表明兩個變量間不是線性相關[2]。
本文通過計算2011年我國火災起數、火災直接損失(萬元)和火災燒毀建筑(m2)的統計數據中第一位數字頻率分布與Benford定律的期望頻率分布的Pearson相關系數,來判斷這三項統計數據與Benford定律分布之間是否存在顯著差異[3],判斷標準見表1。

表1 Person相關系數的判斷標準
通過Excel軟件計算,上述三項統計數據的Pearson相關系數檢驗結果如表2所示,可以看到各項統計數據的Pearson相關系數都在0.98以上,基本可以認為2011年我國消防統計數據中火災起數、火災直接損失(萬元)和火災燒毀建筑(m2)的數據質量較好,不存在明顯的可疑情況。但是在三項統計數據中除了火災直接損失(萬元)的Pearson相關系數大于0.99,表現為完全符合Benford定律,其余兩項統計數據的Pearson相關系數都在0.98左右,也就是說火災起數和火災燒毀建筑(m2)的統計數據質量需要我們加以關注,對這兩項統計數據還要進一步分析確認。
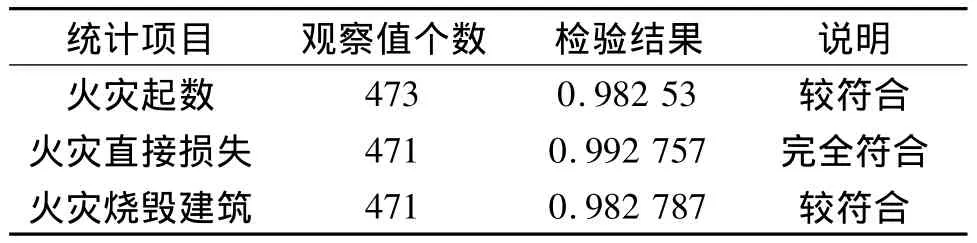
表2 統計數據檢驗結果
4 結論
我國每年的消防統計數據種類較多,覆蓋范圍較大,隨著國家經濟快速發展,各個地區的消防統計數據也呈現出不同的變化。這也是要尋找一種能夠對我國消防統計數據質量進行快速簡便分析的重要原因,本文經過實證研究,表明Benford定律可以較好的滿足上述要求。在數據質量檢驗中引入Pearson相關系數進行數據分析,通過驗檢結果應該相信《中國消防年鑒》(2012)所公布的2011年全國31個省、自治區、直轄市(不包含新疆生產建設兵團)的火災起數、火災直接損失(萬元)和火災燒毀建筑(m2)的統計數據可靠性較高,沒有明顯的質量問題。
[1]公安部消防局.2012中國消防年鑒[M].北京:中國人事出版社,2012.
[2]程廣華.利用 Benford定律在海量數據中篩選非法商戶研究[J].探索論壇,2010,(4).
[3]許存興,王大江,張芙蓉.上市公司審計意見實證分析——基于Benford定律的造假檢測[J].南京大學財經學報,2009,(4).
- 中國人民警察大學學報的其它文章
- 電氣火災統計分析研究
- 淺析聽證制度在消防行政執法中的應用
- 高層建筑利用電梯安全疏散的問題與對策

