彈道修正彈落點預報方法研究

史金光，劉 猛，曹成壯，王中原

（1.南京理工大學 能源與動力工程學院，南京210094；2.海軍駐沈陽彈藥專業軍事代表室，沈陽110045；3.遼沈工業集團有限公司 研發中心設計二所，沈陽110045）

精確打擊技術是彈箭技術重點發展方向之一，為此世界各國均在開展各種大口徑彈箭的彈道修正，對目標實現精確打擊。通常彈道修正彈的修正原理是在彈箭發射前根據觀測的目標坐標等信息預先裝定方案彈道參數，彈箭發射后由探測系統實測空中飛行彈丸的實際彈道，將實測的飛行彈道參數與預先裝定的方案彈道參數進行比較，獲得彈道偏差，根據偏差的大小和方向形成修正指令，控制彈上的執行機構進行距離和方向修正［1－3］。這種修正原理過多依賴實測飛行彈道參數和預先裝定方案彈道參數的精度，對于大口徑彈箭，通常采用衛星定位裝置或跟蹤雷達等進行飛行彈道參數的測量，其測試誤差較大，如目前衛星定位裝置的坐標和速度測量精度分別約為σx≤10m，σy≤15m，σz≤10m 和σv≤0.2m／s，同時預先裝定的方案彈道易受各種因素的影響，這樣就會造成最后計算得到的彈道偏差誤差較大，影響其修正效果。

為此，本文針對上述情況，對大口徑彈道修正彈，不采用預先裝定方案彈道的途徑，而是利用探測系統對空中飛行彈丸實測的一段飛行彈道參數進行彈道濾波，辨識出其實際阻力和升力符合系數，然后利用外推彈道模型預報出實際彈丸落點，與觀測的目標坐標信息比較，獲得彈道偏差，為修正指令的生成提供了依據。該方法一方面未使用方案彈道參數，避免了一些隨機因素（如風等）對方案彈道的影響，另一方面利用空中飛行彈丸的一段實測彈道參數進行了空氣動力參數的辨識，通過外推彈道模型預報彈丸落點，是理論模型與實測數據相結合的一種動態預報方法。

1 彈道修正彈飛行原理

彈道修正彈發射后，探測系統對其一段飛行彈道參數進行測量；信息處理系統利用實測飛行彈道參數進行彈道濾波，辨識出其實際阻力和升力符合系數，然后利用外推彈道模型預報出實際彈丸落點，獲得與目標坐標的偏差修正量，形成修正控制指令，在飛行彈道適時位置處控制執行機構動作，調節彈道，實現彈道修正，提高其射擊精度。其彈道原理圖如圖1所示。

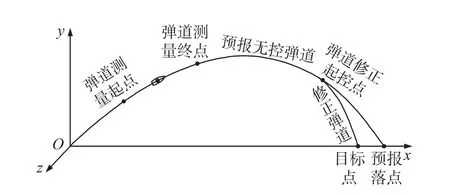
圖1 彈道原理圖

2 外推彈道解算模型

根據彈道修正彈的飛行原理，信息處理系統需對測量彈道參數進行彈道濾波，辨識出其實際阻力和升力符合系數，并對其后續飛行彈道進行預報，因此在上述過程中需要用到理論彈道模型，考慮到彈道修正彈落點解算的快速性、實時性和探測系統可提供的測量參數，及其預報的彈道落點要同時滿足射程和側偏精度等因素，需選取合適的簡化彈道模型。由外彈道理論知［4－5］，當彈軸運動形成攻角時立即產生升力和馬格努斯力，升力和馬格努斯力都垂直于速度，前者在攻角平面內，后者與攻角平面垂直。在彈道彎曲時右旋彈產生了向右的動力平衡角δ2p和向上（或向下）的動力平衡角δ1p。由δ2p產生向右的升力和向上的馬格努斯力，由δ1p產生向上（δ1p＞0時）或向下（δ1p＜0時）的升力和指向左（δ1p＞0時）或向右（δ1p＜0時）的馬格努斯力。它們將使質心速度方向改變，進而使彈道發生扭曲，產生側偏并影響射程。由于向右的動力平衡角δ2p?δ1p，故相應地升力主要指向右方，從而使彈道右偏，形成偏流。因此，彈丸的側向運動（偏流）主要是由動力平衡角δ2p形成的升力產生的，為此，本文采用考慮動力平衡角影響的質點彈道模型作為彈道濾波和外推彈道的狀態方程。

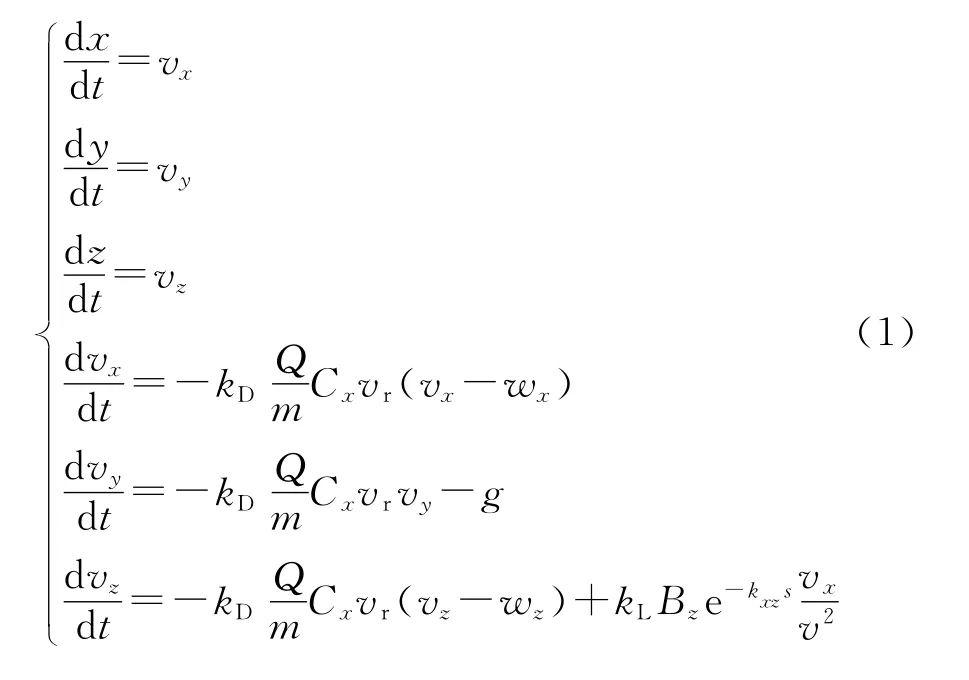
式中：x，y，z，vx，vy和vz分別為彈丸在地面坐標系中的坐標分量和速度分量；kD和kL為阻力和升力符合系數；m，Cx，g，wx和wz分別為彈丸質量、空氣阻力系數、重力加速度、縱風和橫風；Q＝ρπd2／8，ρ為空氣密度，d為彈徑；為彈丸速度和相對速度。

3 擴展卡爾曼氣動參數辨識彈道模型

由彈道修正彈的飛行原理可知，探測系統需測量空中彈丸的一段飛行彈道參數，通常可以直接（如采用衛星定位裝置）或間接（如采用跟蹤雷達，由實測的斜距離、高低角和方位角換算得到）測得彈丸在空中飛行的3個坐標分量x、y、z和3個速度分量vx、vy、vz。利用這6個量測參數和式（1）要辨識出空中飛行彈丸的主要氣動參數，即阻力和升力符合系數kD和kL。為此，需利用測量的一段彈道參數（即量測值）和理論彈道模型式（1）構造氣動參數辨識彈道模型。

取x、y、z、vx、vy、vz、kD、kL作為彈道濾波的狀態變量。令：

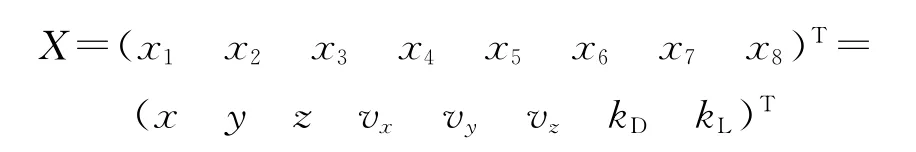
于是方程組（1）可寫成：

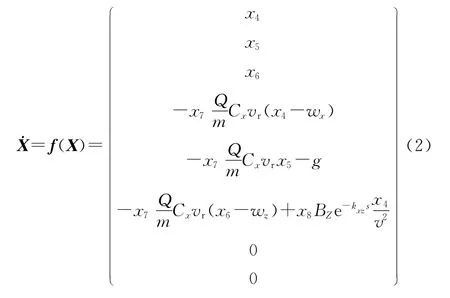
由式（1）和式（2）可見，解算該質點彈道模型屬于非線性估計問題，而擴展卡爾曼濾波正是針對非線性系統，并結合標準卡爾曼濾波算法提出的一種次優估計算法［6－7］。根據擴展卡爾曼理論，對該質點彈道模型的狀態方程和量測方程進行線性化、離散化處理，可得到擴展卡爾曼氣動參數辨識彈道模型。

預測方程：

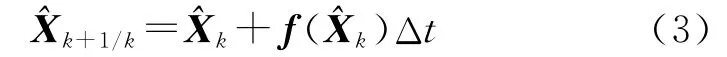
預測方差：

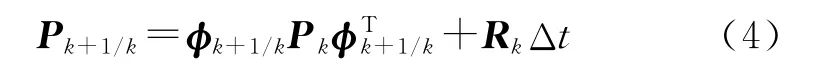
量測方程：

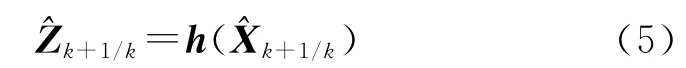
式中：h（）為量測參數矩陣。

濾波方程：

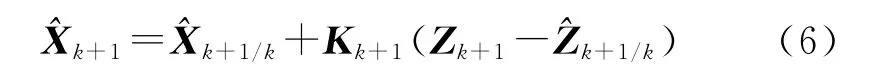
加權矩陣：

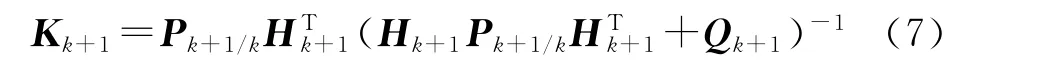
濾波方差：

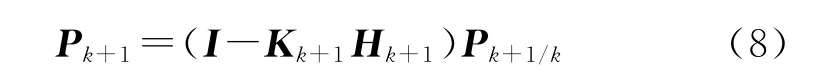
濾波初值：

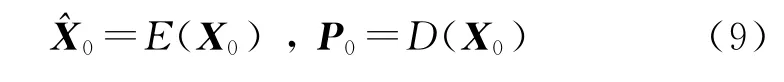
4 數值計算分析

本文以某大口徑彈道修正彈為算例，利用衛星定位裝置對算例實測的一段飛行彈道參數，采用文中所述方法進行氣動參數辨識，及進行后續飛行彈道落點（Xyc，Zyc）的預報，并與靶場實測彈丸落點（Xc，Zc）比較，獲得預報彈道落點誤差（ΔXc＝Xyc－Xc，ΔZc＝Zyc－Zc）。衛星定位裝置的坐標測量誤差約為σx≤10m，σy≤15m，σz≤10m，速度測量誤差約為σv≤0.2m／s。

圖2給出彈道側偏的實測值與濾波值，圖3給出擴展卡爾曼濾波過程中的坐標濾波方差，圖4、圖5給出彈道濾波過程中辨識出的阻力和升力符合系數。由圖2可知，探測系統測量的彈道參數具有較大的測量噪聲，但經擴展卡爾曼彈道濾波后，能有效剔除其測量噪聲，濾波值能很好地反映出測試的彈道規律。由圖3～圖5可知，在擴展卡爾曼彈道濾波過程中，坐標濾波方差衰減很快，阻力和升力符合系數逐漸收斂，經6s彈道濾波后坐標濾波方差、阻力和升力符合系數趨于穩定。

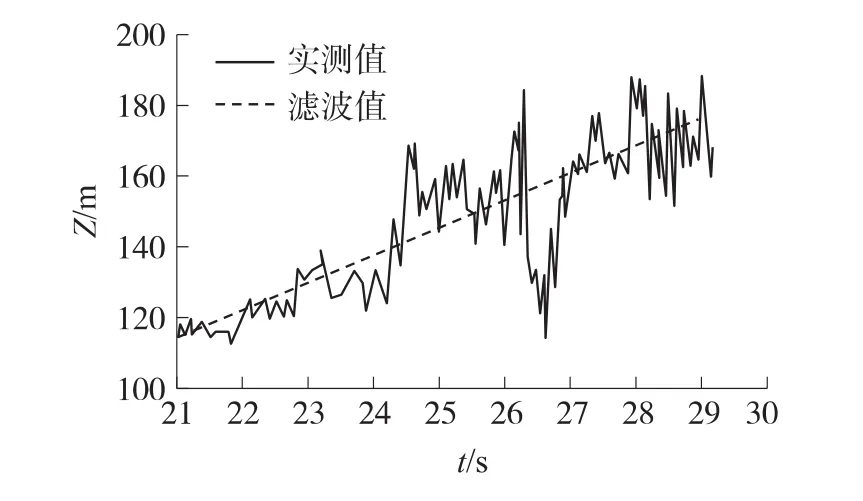
圖2 彈道側偏的實測值與濾波值

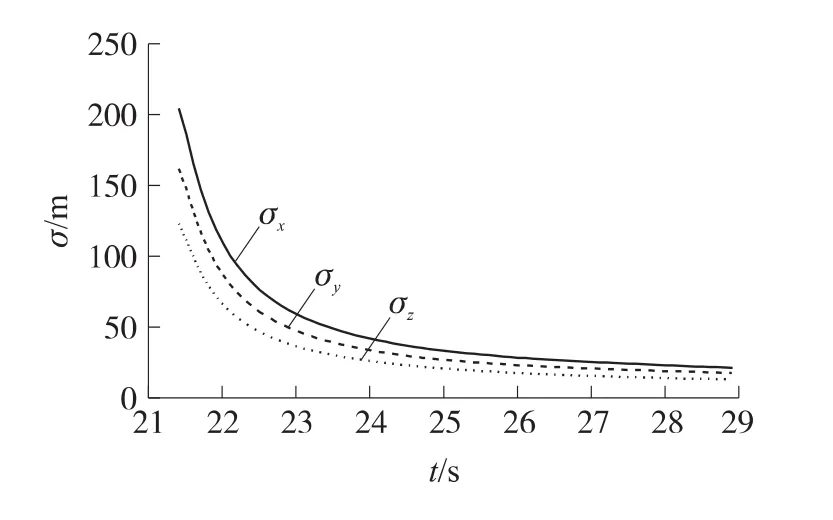
圖3 擴展卡爾曼濾波過程中的坐標濾波方差

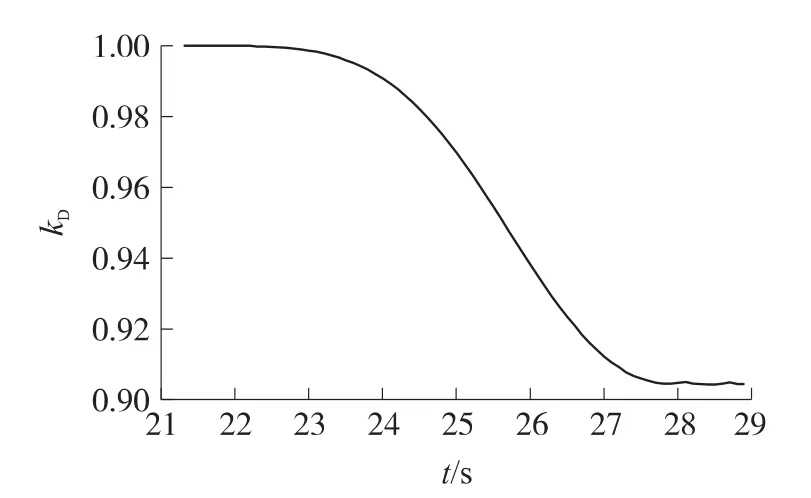
圖4 辨識的阻力符合系數kD

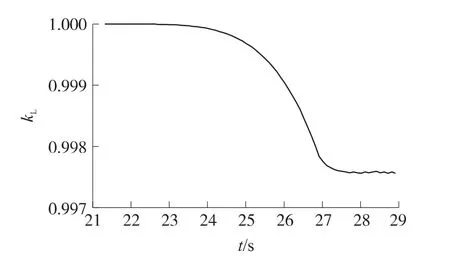
圖5 辨識的升力符合系數kL

表1給出預報彈道落點誤差隨飛行彈道參數測量時間的變化關系。由表可知，預報彈道落點精度隨著測量時間的增加而迅速提高，但經過一段測量時間后，這種趨勢逐漸變緩，當測量時間超過6s時，預報彈道落點已非常接近實測彈道落點，這主要是因為擴展卡爾曼氣動參數辨識彈道模型根據每一實測彈道點均進行彈丸的氣動參數辨識，當測量時間超過6s時，辨識的阻力和升力符合系數kD、kL已逐步收斂，并趨于某穩定值（如圖4和圖5所示）。因此，在滿足彈道修正彈的預報彈道落點精度條件下，不宜過分地增加飛行彈道的測量時間，因為測量時間的增加，將會帶來彈道解算時間的增加，而落點精度的提高卻有限。

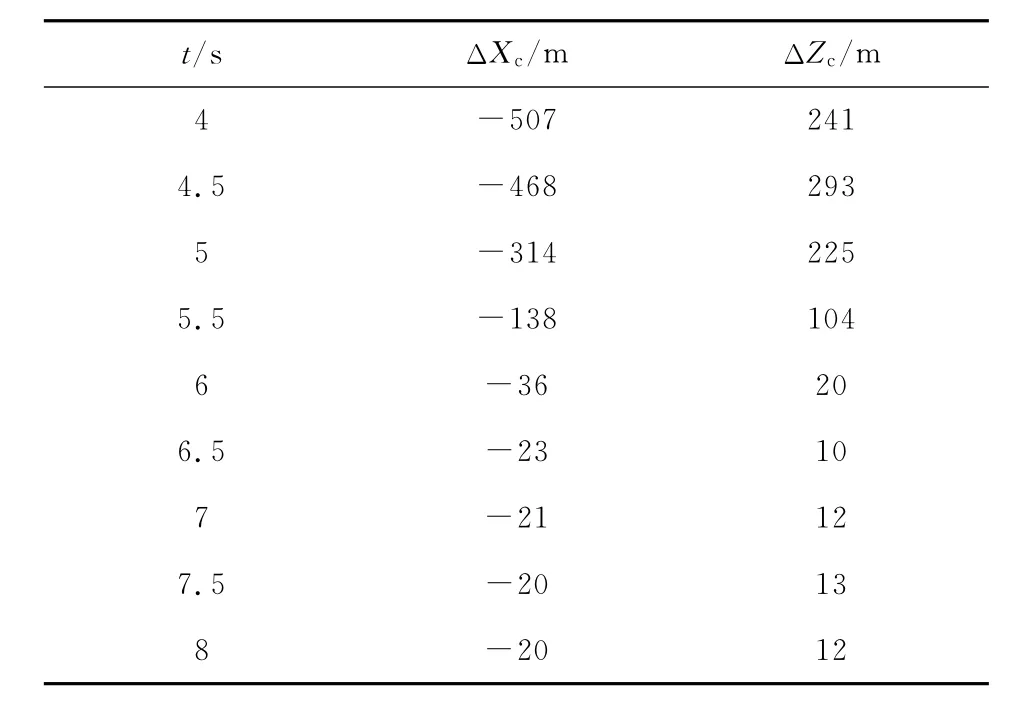
表1 預報彈道落點誤差隨飛行彈道參數測量時間的變化關系（Δt＝100ms）

表2給出預報彈道落點誤差與采樣時間間隔的關系。在一定的飛行彈道參數測量時間條件下，采樣時間間隔越小，測量的彈道參數點數越多。

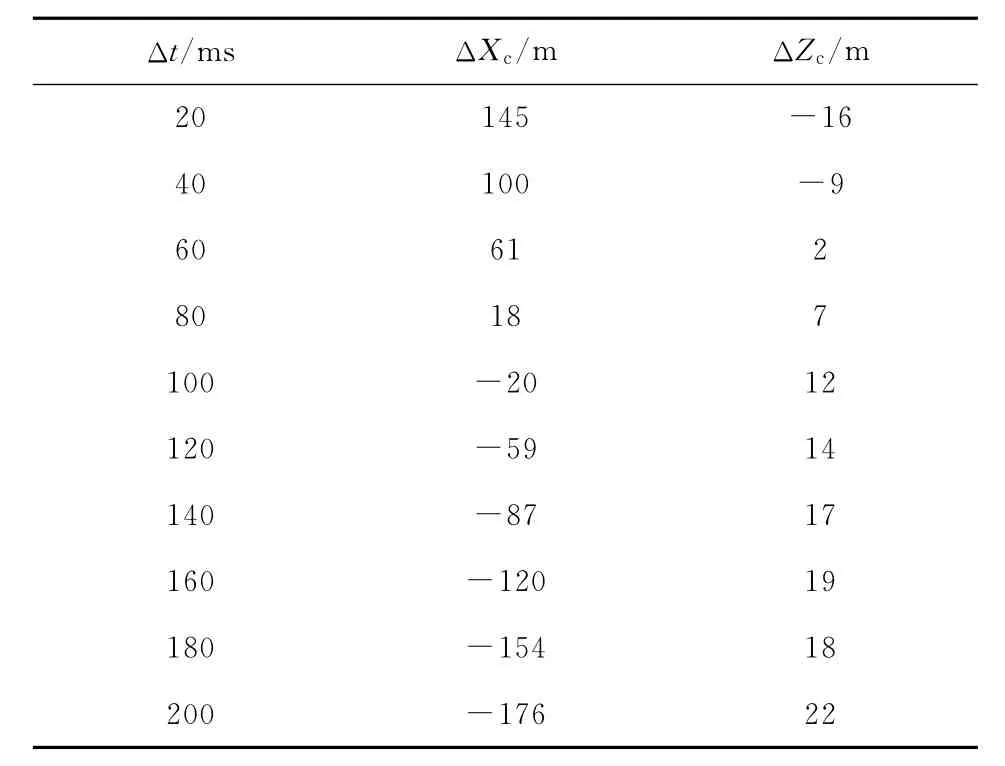
表2 預報彈道落點誤差與采樣時間間隔的關系（飛行彈道參數測量時間為8s）

由表2可知，并不是隨著采樣時間間隔越小和測量點數越多，預報彈道落點精度就越高，而是存在一合適的采樣時間間隔范圍（如60～120ms），這是因為擴展卡爾曼氣動參數辨識彈道模型根據每一實測彈道點進行氣動參數辨識時，過小的采樣時間間隔，盡管測量點數較多，但在每一小段上對飛行彈丸彈道特性的綜合影響不能很好地體現，辨識出的氣動參數誤差較大；過大的采樣時間間隔，盡管在每一小段上能較好地反映出彈丸在該測量段上的彈道特性，但由于測量點數較少，彈道濾波處理的有效彈道段數少，綜合辨識出的氣動參數誤差也較大。因此，對于確定的飛行彈道參數測量時間，選取合適的采樣時間間隔對預報彈道落點精度和彈道解算時間均是有利的。

5 結束語

本文針對彈道修正彈預裝方案彈道參數實施彈道修正可能存在的問題，提出利用實測的一段飛行彈道參數進行彈道濾波與氣動參數辨識，并預報后續彈道落點的實時彈道解算方法。數值計算結果表明，經擴展卡爾曼彈道濾波后，能有效剔除測量彈道參數的噪聲，且坐標濾波方差、阻力和升力符合系數逐漸收斂，經6s彈道濾波后坐標濾波方差、阻力和升力符合系數已趨于穩定；預報彈道落點精度隨著飛行彈道參數測量時間的增加而迅速提高，但經過一段測量時間后，這種趨勢逐漸變緩，考慮到實時彈道解算方法的預報彈道落點精度和彈道解算時間等，測量時間宜取6～8s；預報彈道落點精度并不是隨著采樣時間間隔越小，測量點數越多，預報精度越高，而是存在一合適的采樣時間間隔范圍。

［1］李東光，周國勇，馬寶華.一維彈道修正引信彈道敏感技術［J］.兵工學報，2003，24（3）：309－312.LI Dong－guang，ZHOU Guo－yong，MA Bao－hua.Trajectory susceptivity for a one－dimensional trajectory correction fuze［J］.Acta Armamentarii，2003，24（3）：309－312.（in Chinese）

［2］吳日恒，郭澤榮.射程修正引信彈道辨識方法及精度分析［J］.彈道學報，2008，20（1）：43－47.WU Ri－heng，GUO Ze－rong.Method and precision analysis of the trajectory identification of range correction fuze［J］.Journal of Ballistics，2008，20（1）：43－47.（in Chinese）

［3］申強，李世義，李東光.一維彈道修正引信基于速度－時間序列的彈道辨識［J］.探測與控制學報，2004，26（1）：41－44.SHEN Qiang，LI Shi－yi，LI Dong－guang.A method of ballistic trajectory identification for CCF based on sequence of velocitytime［J］.Journal of Detection and Control，2004，26（1）：41－44.（in Chinese）

［4］韓子鵬.彈箭外彈道學［M］.北京：北京理工大學出版社，2008：175－180.HAN Zi－peng.Exterior ballistics of projectiles and rockets［M］.Beijing：Beijing Institute of Technology Press，2008：175－180.（in Chinese）

［5］史金光，王中原，常思江.基于減旋控制的側向彈道修正技術研究［J］.彈道學報，2010，22（3）：81－85.SHI Jin－guang，WANG Zhong－yuan，CHANG Si－jiang.Technology of lateral trajectory correction based on spin velocity reduction control［J］.Journal of Ballistics，2010，22（3）：81－85.（in Chinese）

［6］徐明友.高等外彈道學［M］.北京：高等教育出版社，2003：152－178.XU Ming－you.Advanced exterior ballistics［M］.Beijing：High Education Press，2003：152－178.（in Chinese）

［7］巫春玲，韓崇昭.用于彈道目標跟蹤的有限差分擴展卡爾曼濾波算法［J］.西安交通大學學報，2008，42（2）：143－146.WU Chun－ling，HAN Chong－zhao.Finite－difference extended Kalman filtering algorithm for ballistic target tracking［J］.Journal of Xi’an Jiaotong University，2008，42（2）：143－146.（in Chinese）