FSC賽車車架結構有限元分析

孫博文，韓忠浩，王曉怡，胡振凱

（遼寧工業大學，遼寧 錦州 121001）

FSC賽車車架結構有限元分析

孫博文，韓忠浩，王曉怡，胡振凱

（遼寧工業大學，遼寧 錦州 121001）

車架是汽車的重要組成之一，它必須滿足在各種工況下的強度和剛度要求，車輛才能正常行駛。對賽車而言更是如此。本文首先建立了遼寧工業大學2014年賽車車架的三維模型；然后導入到ANSYS workbench軟件中，建立有限元模型，通過對有限元模型進行約束、加載，來模擬賽車在各工況下的運行情況；最后查看計算結果，判斷車架是否滿足要求。因此，各工況的強度、模態分析結果，對賽車的安全以及保證正常行駛具有重大意義。

FSC賽車車架；強度及剛度分析；模態分析；有限元分析

CLC NO.: U463.3 Document Code: A Article ID: 1671-7988(2015)03--

引言

中國大學生方程式汽車大賽（簡稱FSC）是由各高等院校汽車專業的在校學生組隊參與設計與制造的比賽。所設計的賽車需滿足大賽規則要求。

賽車車架作為各部件的安裝載體，其安全性是賽車能否行駛的保證，也是保護車手安全的前提。本文利用Ansys workbench對車架模型進行有限元分析。

1、賽車車架模型的建立

賽車車架是按照FSC大賽規則設計的空間桁架，是由壁厚不同、長短不同的鋼管焊接而成的。所設計的車架結構需要滿足兩方面的要求：（1）車架要有一定的強度和剛度來裝配賽車上的其他總成；（2）車架的固有振動頻率需要能避開各種激勵頻率，得到合理的動態特性，避免發生共振[1]。本文利用CATIA軟件建立車架模型（如圖1）。

2、賽車車架有限元模型的建立

2.1 模型修復

將已建立的車架模型導入到ANSYS workbench軟件中，可以看到有的連接桿件之間產生了縫隙（如圖2），這將導致劃分的網格出現節點不共享的現象（如圖3），從而影響接下來的分析。

這樣的連接關系與實際不符，應對模型進行修改。利用Joint工具可將桿件連接起來。對修復后的模型進行分網，發現模型中網格節點共享（如圖4），符合實際。

2.2 材料選擇以及網格劃分

由于4130鋼具有高強度和高韌性，所以本車架采用此材料。4130鋼材料屬性主要有密度7.85×103kg/m3，彈性模量211GPa，泊松比0.279，屈服極限785MPa。

考慮到網格精度和計算時間的平衡問題，所以在劃分網格時，單元尺寸選定為5mm，單元類型選用殼單元進行分網。單元形態是以大量四邊形網格為主，以少量三角形網格為輔組成的。并根據桿件設定厚度。最終得到了車架的有限元模型（如圖5）。整個車架的共劃分為112540個單元及110081個節點。

劃分好的網格需要對它的質量進行檢查，高質量的網格會得到高質量的結果。Workbench中對網格質量的檢查項目主要有：Element Quality、Skewness、Aspect Ratio。這些檢查項目代表的意義如表1。查看本車架的網格質量檢查項目（圖6），可以看出所劃分的網格滿足各檢查項目的要求。

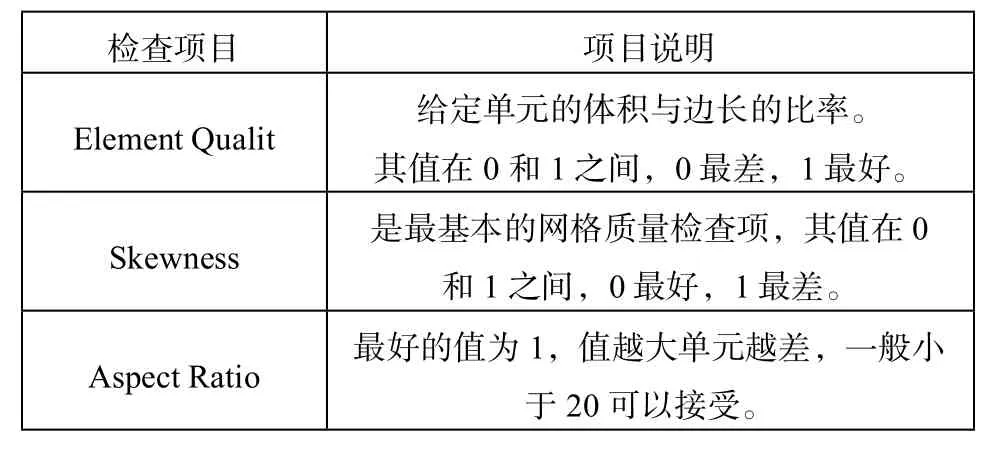
表1 [2]work bench中網格檢查項目及說明

3、車架的強度分析

根據國家標準 GB/T 13043—1991 中規定∶ 樣車必須以一定車速在各種道路上行駛一段里程。 典型工況是高速道路、強扭轉道路和一般道路及彎曲道路上的彎曲、扭轉、緊急制動和急轉彎等 4 種工況[3]。本文將對上述4種工況進行模擬，驗證車架的強度是否符合要求。

3.1 車架的靜態載荷

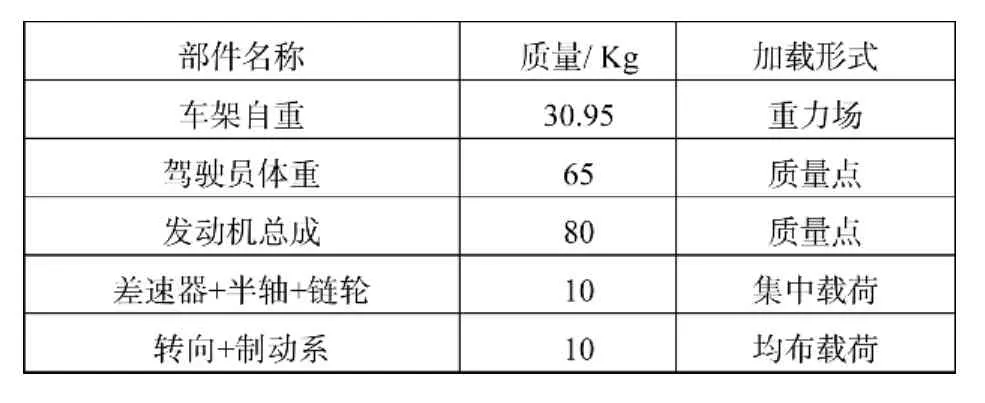
表2 各部件的質量及加載形式

車架所受到的靜態載荷指的是作用到車架上各部件所產生的重力。主要包括車架自重、駕駛員體重、發動機總成質量等。將所有質量換算為重力，施加到車架的相應位置上。各部件的質量及加載形式如表2所示。

3.2 彎曲工況

彎曲工況指的是賽車在水平良好路面上勻速直線行駛或靜止狀態。為更好的對工況進行模擬，需將靜載荷乘上一個動載系數，一般為2.0～2.5，本文取2.0。

約束情況：以賽車前進方向為X軸，橫向為Y軸，垂直方向為Z軸。對前懸架右連接點進行固定約束，對前懸架左連接點進行X、Z方向的約束，對后懸架左、右連接點處進行Z方向的約束。

經過加載和約束后，運行程序進行計算，并得到相應的應力云圖和位移云圖。結果如圖7、圖8所示。從圖7中可以看出最大應力為169MPa，發生在車架前環底部多桿焊接處，小于屈服極限。從圖8可以看出最大位移量為1.26mm，發生在座艙底部交叉桿處。因此，彎曲工況下的車架強度滿足要求。

3.3 扭轉工況

扭轉工況指的是一側車輪懸空時，所受到的扭矩使車架產生扭轉現象。本文模擬前懸架左側連接點施加向上647N的集中力，前懸架右側連接點施加向下647N的集中力。實踐表明，車架承受最劇烈的扭轉工況是在汽車低速通過崎嶇不平路面時發生的。由于車速較低，故取動載系數為1.5[4]。

約束情況：對后懸架左連接點進行固定約束，對后懸架右連接點進行X、Z方向的約束。釋放前懸架的連接點。

計算得到扭轉工況下的應力、位移云圖。結果如圖9、圖10所示。

從圖9可以看出最大應力為119MPa，發生在座艙底部多桿連接處。從圖10可以看出最大位移量為0.94mm，發生在座艙底部的交叉桿上。因此，車架在扭轉工況下滿足要求。

3.4 制動工況

制動工況指的是剎車的情況。賽車在行駛過程中需要頻繁的制動，駕駛員和發動機除了受到垂直方向的載荷外，還受縱向慣性力的作用[5]。此慣性力通過設置慣性加速度a=1.4g方式進行加載，其方向沿縱向向前。

約束情況：對前懸架左、右連接點進行固定約束，對后懸架左、右連接點的Y、Z方向進行約束。

從圖11可以看出最大應力為164MPa，發生在主環座艙底部多桿相交處，小于屈服極限。從圖12可以看出最大位移量為0.81mm，發生在座艙底部相交桿處。因此，車架在制動工況下強度滿足要求。

3.5 急速轉彎工況

賽車在轉彎行駛時，車架除了受到靜態載荷的作用外，還會受到由于轉彎產生的離心力作用。本文模擬賽車向左轉彎，離心加速度為10.9m/s2，沿橫向向右。

約束情況：對前懸架左、右連接點進行固定約束，對后懸架左、右連接點的X、Z方向進行約束。

從圖13可以看出，最大應力為205.69Mpa，發生在座艙底部交叉桿與側防撞桿的交叉位置。圖14中最大位移為0.99mm，發生在座艙交叉處。滿足要求。

4、剛度分析

剛度表示車架在外力下抵抗變形的能力，也是衡量車架性能的重要指標。

4.1 車架的彎曲剛度

為了節約計算時間，可將車架簡化成圖15所示簡單的梁結構。把集中載荷1471.5N分別作用到車架兩側的縱向中點位置，方向垂直向下。約束情況與彎曲工況相同。通過計算得到位移云圖（圖16），從中找到最大位移量。

從圖16中得到Z方向的最大位移量為0.48mm。將所有數據帶入下列公式（1）中，就可算出車架的彎曲剛度。

F—集中載荷，N

L—車架前后懸架間的距離，m

f—加載點的撓度，m

本車架的彎曲剛度為2.37× 105Ng m2，查閱相關資料發現本車架的彎曲剛度合理。

4.2 車架的扭轉剛度

將車架前艙視為如圖17的梁結構，左懸架連接點施加-647N的集中載荷，右懸架連接點施加647N的集中載荷。約束同扭轉工況相同。運行程序，從位移云圖可以查看到最大位移量為0.39mm（圖18）。

根據扭轉后的最大位移量和前艙寬度B可以求出扭轉角θ

根據施加集中載荷F和前艙寬度B可求出轉矩T

根據轉矩T和扭轉角θ可求扭轉剛度E

本車架的扭轉剛度為1302.7Ng m/°，查詢國外賽車設計資料可知，大多是扭轉剛度在1000～4000Ng m/°[3]。本車架的扭轉剛度在此范圍內，因此合理。

5、車架的模態分析

賽車在行駛時，會受到來自路面不平度、發動機振動以及輪胎動態不平衡的激振。如果這些激振的頻率與車架的固有頻率相接近，則會發生共振，導致車架破壞。因此，分析車架的固有頻率和振型是有必要的。

利用modal模塊對車架進行模態分析，首先對模型進行分網，然后設置所要分析的階數，運行程序得出所需要的頻率和振型。車架的固有頻率及振型特點如表3所示，第一階的固有頻率接近0，記錄非零頻率開始的六階頻率。

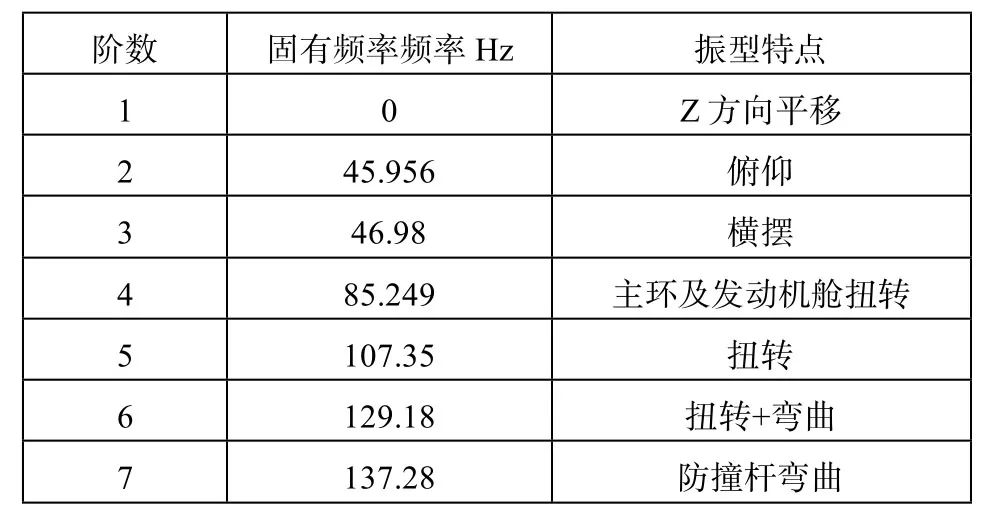
表3 模態分析固有頻率及振型特點

激振中由于路面不平的頻率一般為1～20HZ，車輪不平衡引起的頻率一般低于11HZ。本賽車采用的發動機最高轉速為12500r/min，常用轉速為5000～7000r/min，怠速為2000r/min。根據發動機頻率計算公式

z——發動機缸數；

τ——發動機沖程數

n——發動機轉數。

由公式（5）可知常用發動機引起的激振頻率為167～233HZ，怠速頻率為66.7HZ。發動機怠速頻率介于第三階與第四階頻率之間，而所有頻率都小于發動機常用頻率范圍。因為車架的振動頻率避開了激振的頻率，所以本車架安全可靠，不會有引起共振的危險。

6、結論

通過對遼寧工業大學2014年賽車車架進行強度、剛度和模態分析，得到了車架在4種工況下的應力、位移云圖與彎曲、扭轉剛度，以及車架的前6階固有頻率。結果表明，本車架在強度方面，能夠抵抗破壞，滿足安全要求；在剛度方面，能夠抵抗變形，保證性能良好；在模態分析方面，車架的頻率避開了激振的頻率，避免了車架發生共振破壞的危險。同時可在結果中找出強度、剛度的富裕部位，為車架的優化設計提供理論依據。

[1] 周永光，陽林，吳發亮.FSAE 賽車車架結構優化和輕量化[J].農業裝備與車輛工程,2012.

[2] 賀紹華.賽車輕量化系統方法與車架優化[D].廣東：廣東工業大學,2013.

[3] 趙帥，隰大帥，王世朝，陸善.FSAE賽車車架的強度和剛度分析[J].計算機輔助工程,2011.

[4] 刁秀永,魯植雄，鐘文軍，謝鵬.基于ANSYSWorkbench的FSAE車架有限元分析[J]. 農業裝備與車輛工程,2013.

[5] 喬邦. 基于有限元分析的大學生方程式賽車車架結構強度優化[D].河南：河南科技大學.

The Finite Element Analysis of FSC Racing Frame Structure

Sun Bowen, Han Zhonghao, Wang XiaoYi, Hu Zhenkai
（Liaoning University Of Technology, Liaoning Jinzhou 121001）

A frame is the main component of a vehicle. It must meet the requirements of strength and stiffness under driving conditions.the vehicle can be driven normally. Thus, it is also important to the racing car. In this paper, the author firstly established the three-dimensional frame model of the racing car of Liaoning University of Technology in 2014. Then establishing the finite element model by importing the frame model to ANSYS workbench software and simulating the racing car under different conditions by adding constrain and loads to the model. At last, determining the frame whether the simulation result fulfills its purpose. Therefore, the analysis of the strength and modal under different conditions is very meaningful for the safety and normally driving of the car.

FSC Racing Frame; strength and stiffness analysis; modal analysis; finite element analysis

U463.3

A

1671-7988(2015)03--

孫博文，就職于遼寧工業大學，汽車與交通工程學院。