三體滑行艇縱向運動穩定性的數值模擬
鄒 勁 王瑞宇 孫寒冰 蔣 一
(哈爾濱工程大學 船舶工程學院 哈爾濱150001)
引 言
高速三體滑行艇是常規滑行艇、高速多體船和氣膜減阻船的組合船型,綜合以上幾種船型的優點,在高速滑行時,片體底部與水面接觸,艇體產生的興波與噴濺迅速被吸入槽道內,槽道內會形成氣相區域、液相區域、氣液二相混合區以及噴濺水層,在一定程度上減小了滑行阻力而且還提供了減震、緩沖的作用[1],但也使其運動機理變得較為復雜,尤其是在高速航態下的“海豚運動”。目前,對于常規滑行艇縱向運動穩定性的理論判定方法是通過研究運動微分方程解的穩定性來判斷系統的穩定性[2],但是三體滑行艇底部復雜的結構使求解其在時域內任意時刻艇底的水流體動升力及力矩變得極為困難。而在CFD 領域,由于主要解決兩相流問題,要求在自由液面附近的網格具有很高的分辨率,這一特殊性使商用軟件在船舶六自由度運動具有較大航態變化的高性能船舶,如快艇、高速復合船方面的模擬具有局限性。然而重疊網格的出現使結構網格的自動化成為可能,也使得以上難題獲得解決[3],尤其是在非結構重疊網格技術推廣到包含任意單元類型子網格重疊的情況之后,非結構重疊網格方法可以既具有非結構網格的靈活性,又具有結構重疊網格的計算精度[4]。
借助商業CFD軟件STAR-CCM+,運用結構化背景網格與非結構子域網格相結合的重疊網格方法對某三體滑行艇在高航速下的“海豚運動”現象進行模擬,隨后比照船模試驗結果制定不同重心位置的計算工況,借助二分法對縱向運動穩定性界限曲線進行逼近,計算結果與試驗結果相符,為類似船型的運動預報以及設計優化提供了一定參考。
1 船型簡介
計算船型為某超高速三體滑行艇,主要參數如表1所示。圖1為模型剖線示意圖,縮尺比為1∶5.625,運用CATIA軟件進行建模。

表1 模型參數
2 數值方法
借助商業CFD軟件STAR-CCM+進行仿真計算,使用改進型的Realizablek-ε湍流模型來封閉RANS方程,該方法可較好地模擬存在流動分離和逆壓梯度的復雜流動問題。自由液面處用VOF法進行追蹤。
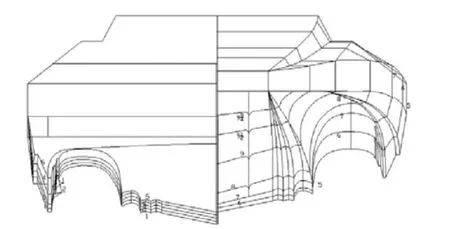
圖1 模型橫剖線示意圖
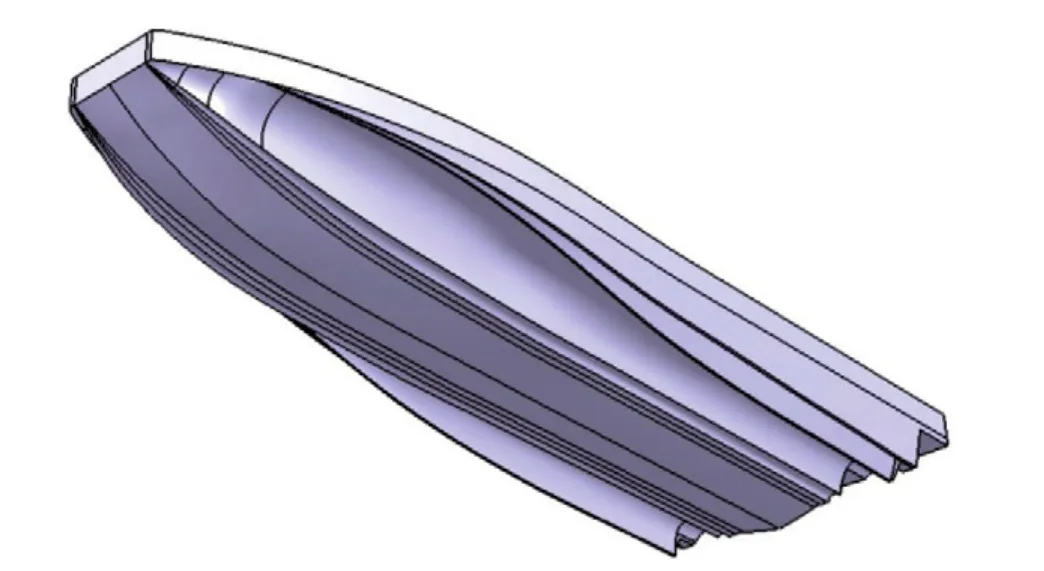
圖2 CATIA模型
運動模擬中采用自由模方法,釋放船舶的升沉和縱搖兩自由度,完全模擬船模在靜水中的直航狀態。船模在拖曳前進時,會對其周圍流場產生影響,使壓力場和剪應力場發生變化,也使船模所受的力和力矩發生變化:
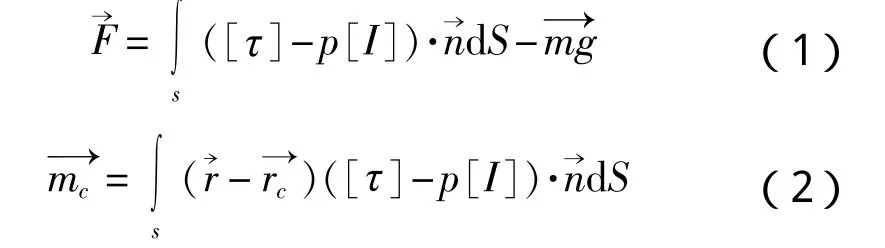
船模剛體的六自由度控制方程為:
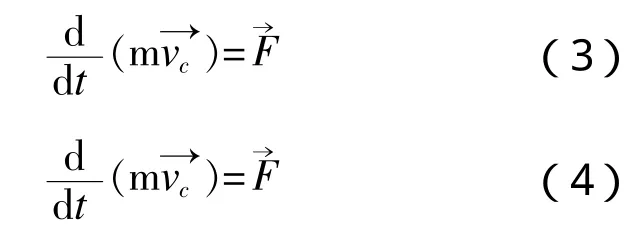
3 網格劃分
采用重疊網格技術,將控制域劃分為主域與子域兩部分,在計算中每迭代一次都需重新記錄交叉在一起的不同兩種網格的信息并讓數值在其中傳遞,雖耗時較長,卻保證了計算對象網格形態的穩定,有利于實現姿態大幅變化的運動模擬[5-6]。
控制域尺寸為:寬為3L,入口距離船尾為3L,出口距離船尾為4L,氣相、液相區各為1.5L。背景網格采用正交結構化網格,子域網格選擇切割體網格(Trimmer),在自由液面處、船體運動范圍內進行網格加密,且加密處網格尺寸與子域網格大致相當。背景網格基準尺寸為0.12倍船長,子域以及加密區域網格基準尺寸為0.012倍船長。
由于三體滑行艇航行速度極快,當越過阻力峰之后雷諾數Re達到107,因此壁面第一層網格厚度會在一定程度上影響計算機結果,邊界層網格的最小尺度可由以下公式[7]求出:
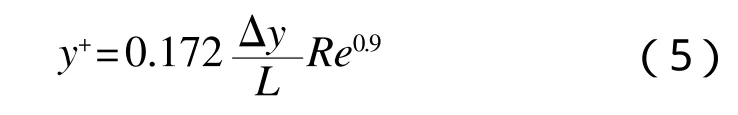
式中:y+代表壁面無量綱距離;Δy表示壁面第一層網格厚度;L為船長;Re表示雷諾數。
以=4,Re=2.79×107為例,邊界層層數設為三層,增長率取1.1,選取不同的y+并且生成四套網格,將平衡后得到縱傾角相對于試驗值的誤差作為依據,以此來確定網格方案。在表2中可以看到方案3誤差較小,因此選擇第三套方案。
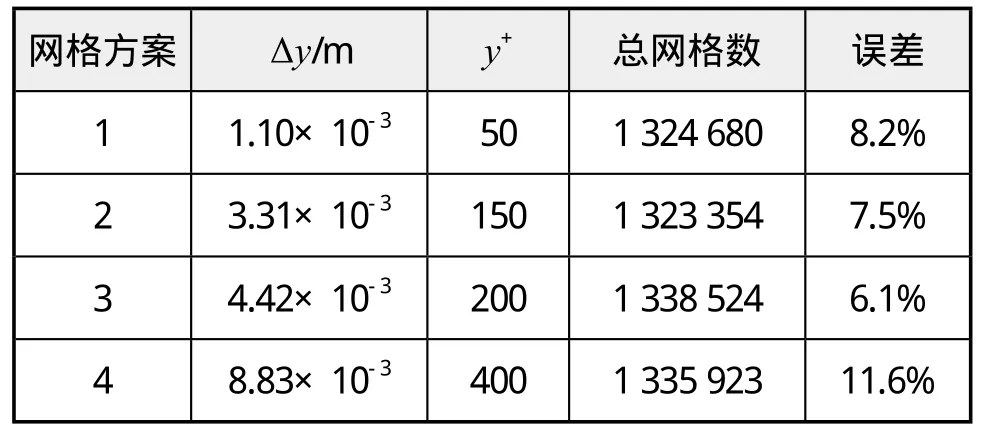
表2 網格方案
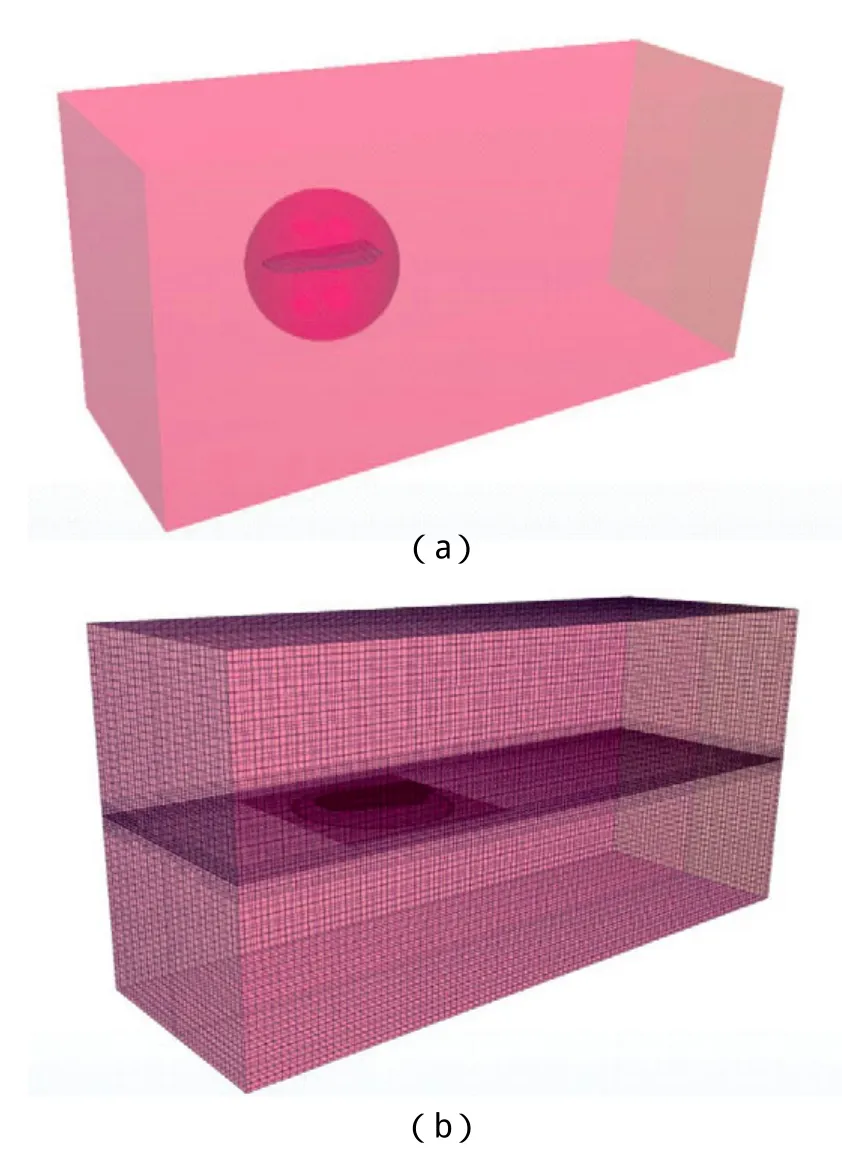
圖3 控制域
4 數值計算與結果分析
4.1 “海豚運動”現象數值模擬
常規滑行艇在靜水中航行時,隨著速度不斷增加,會出現一種周期性、有界的垂直平面內的運動,這是一種垂蕩和縱搖的耦合運動,稱為“海豚運動”[8]。其產生原因主要是隨著速度的增大,滑行艇尾部單位長度上的負荷逐漸加大。盡管垂蕩及縱搖的小幅度變化只引起浸濕長度的微小改變,但是由于速度較大,所以整個水動壓力的變化很大,使得滑行艇難以維持原有平衡。
下頁圖4為當xg= 0.561 5 m,速度v= 10.5 m/s時,不同時刻的艇底壓力分布圖。由圖4(a)可以看到,t= 1.35 s時,水動升力集中在艇尾的一小部分區域,使浸濕長度減小,整體動升力下降,艇體開始下沉并伴隨著埋首。當動浮力點不斷前移并達到平衡時,由于慣性作用,運動并不停止,直到動浮力集中在船艏附近并形成小范圍高壓區,如圖4(b)所示,此時艇體又開始抬首。這一過程循環往復,就形成了周期性的垂蕩與縱搖組合——“海豚運動”現象。

圖4 艇底壓力分布圖(xg = 0.561 5 m,v = 10.5 m/s)
4.2 縱向運動穩定性界限的求解
三體滑行艇的這種縱向不穩定性與 和重心位置xg有關。王慶旭等[9]通過修改重心縱向位置xg、改變航速v對該三體滑行艇的船模進行靜水直航試驗,并將得到的縱向失穩點進行曲線擬合,得到關于的曲線函數,即縱向穩定性界限曲線,其表達式為:

式中:CB=Δ/(ρV2B2/2),表示動負荷系數。
由式(6)可見,若單純增加重心距離尾板的距離xg,失穩的臨界會變大,也就是失穩速度會加大。為了驗證數值計算結果,將數值計算工況與船模試驗對應(文中所有實驗數據均參照文獻[9]),運用“二分法”對四種不同重心縱向位置處的失穩點進行逼近:速度相隔1 m/s,在試驗值附近選取三個工況分別計算,若在所選工況中不存在未失穩點則將工況向下調整0.5 m/s;若包含,則對未失穩點和下一個與其相鄰的工況進行二分繼續計算,精度為0.5 m/s。初始工況如表3所示。
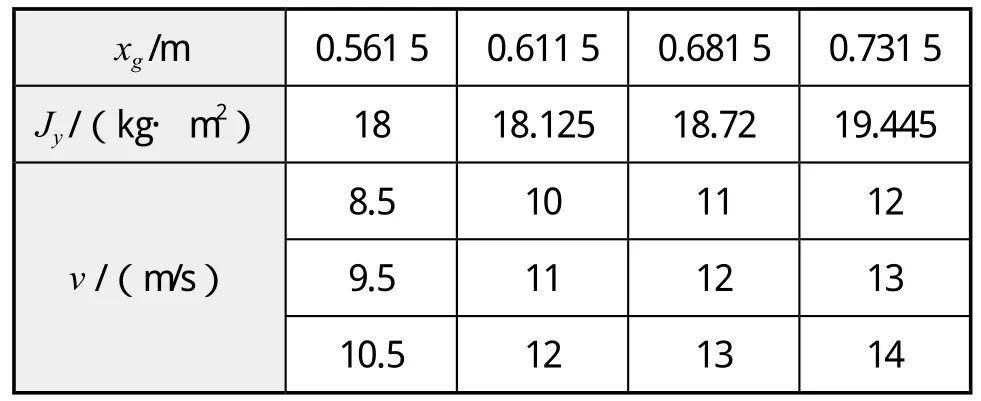
表3 數值計算工況
圖5為垂蕩時歷曲線,下頁圖6為縱搖時歷曲線。
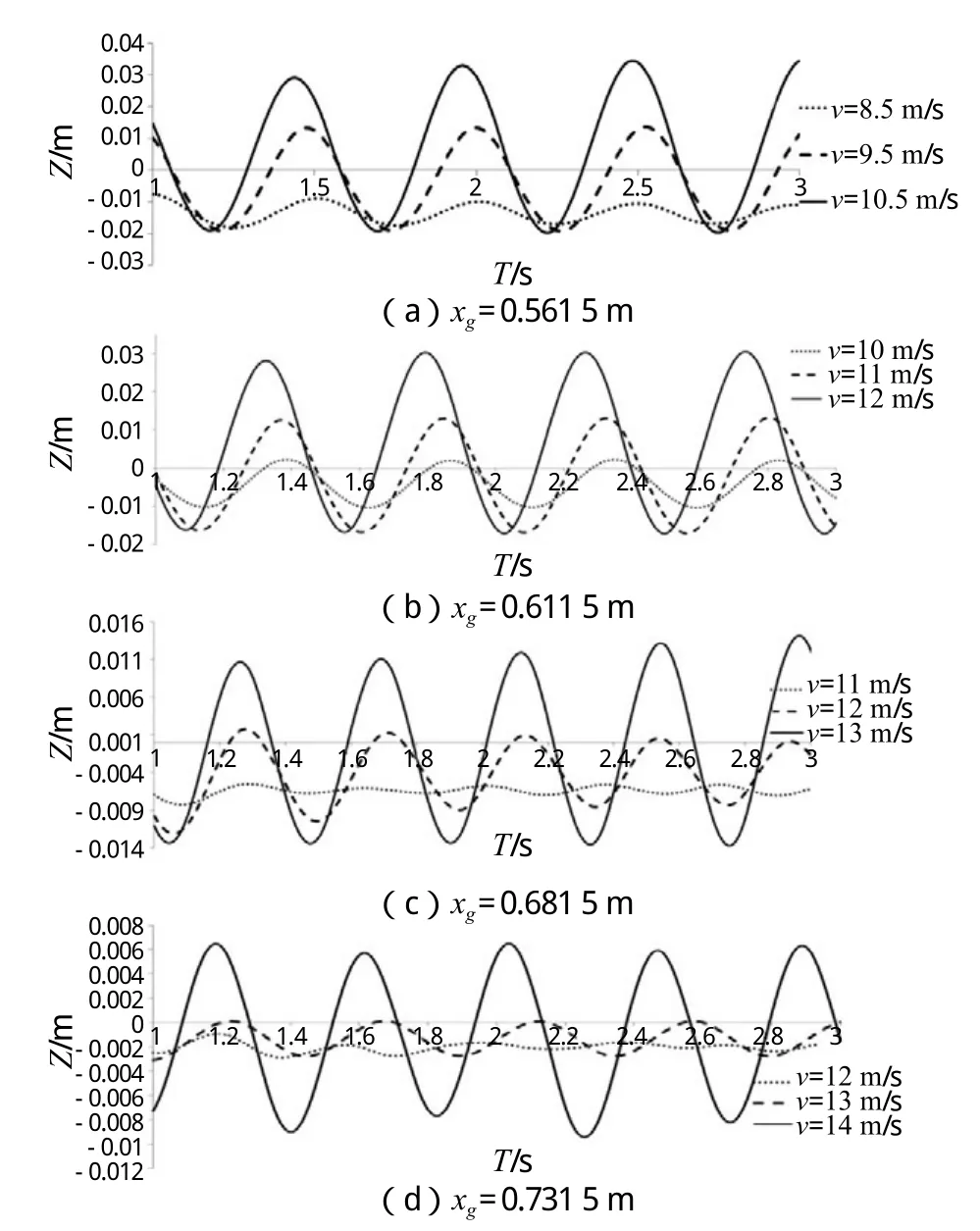
圖5 垂蕩時歷曲線
在圖5(a)、6(a)中可以看到,xg= 0.561 5 m、速度在8.5 m/s時,縱向運動雖有規律,但幅度微小,升沉幅度不足0.01 m,縱搖幅度不到0.5°;當速度從8.5 m/s提升到9.5 m/s時,升沉以及縱搖幅度明顯加劇,升沉幅度達到0.03 m,縱搖2.5°左右。不難看出,xg= 0.561 5 m時,縱向運動失穩點在8.5 m/s之前且就在附近。事實上,將速度降到v= 8.0 m/s時,“海豚運動”消失。同樣,xg= 0.611 5 m時,v= 10 m/s依然失穩;當速度降到9.5 m/s時,海豚運動消失。因此,xg= 0.561 5 m、xg= 0.611 5 m時的臨界失穩速度分別在8.0~8.5 m/s、9.5~10 m/s之間。而另外兩個重心位置,在預先選取的最小速度點處均未出現“海豚運動”,對最小速度點與相鄰速度點進行二分,繼續計算,分別得到未失穩點v= 9.5 m/s、v= 12.5 m/s,將數值結果與實驗結果比較,得到表5。
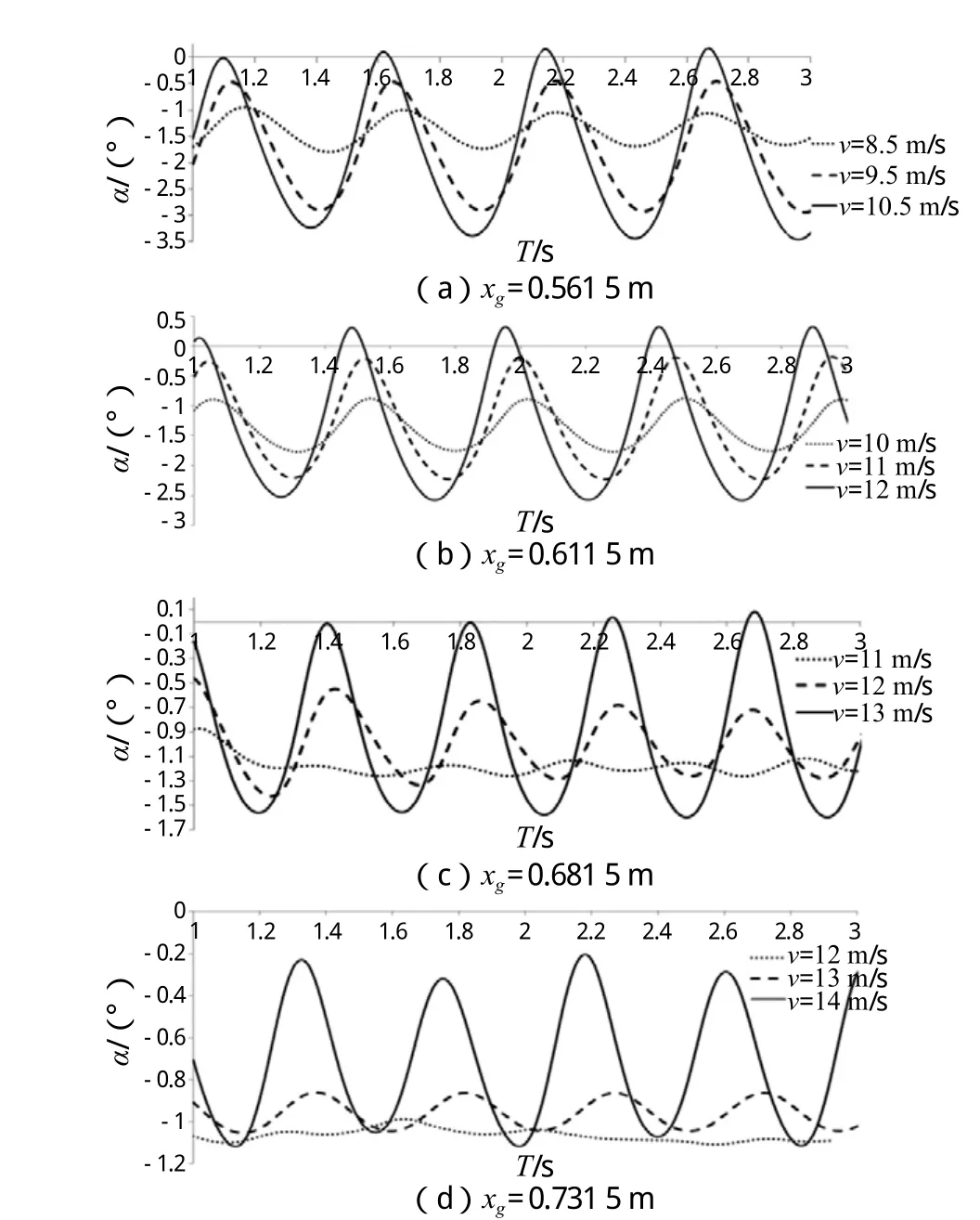
圖6 縱搖時歷曲線
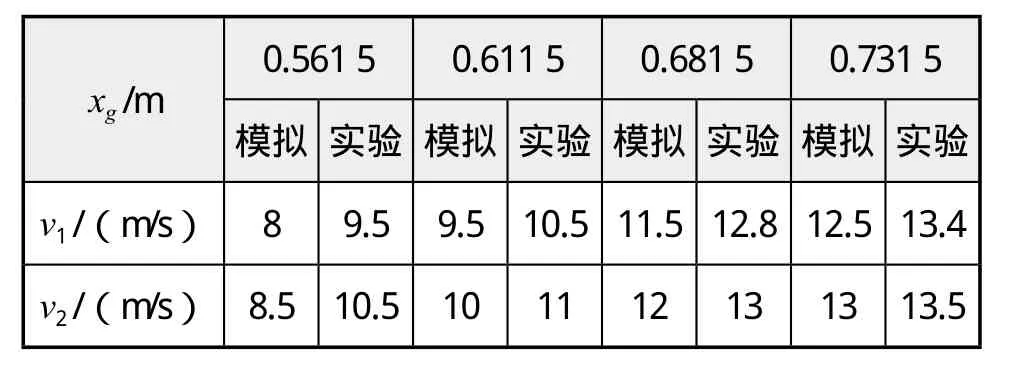
表5 模擬結果與實驗結果
在表5中,v1表示穩定速度上限、v2表示失穩速度下限。從計算結果中看到,隨著重心位置的前移,縱向失穩速度變大,趨勢與實驗結果相吻合。與實驗結果相比,xg= 0.561 5 m時的v2誤差最大,為19%;xg= 0.731 5 m時的v2誤差最小,為3.7%;在其他結果中,除xg= 0.561 5 m時的v1之外,誤差均小于10%。圖7為縱向穩定性界限。
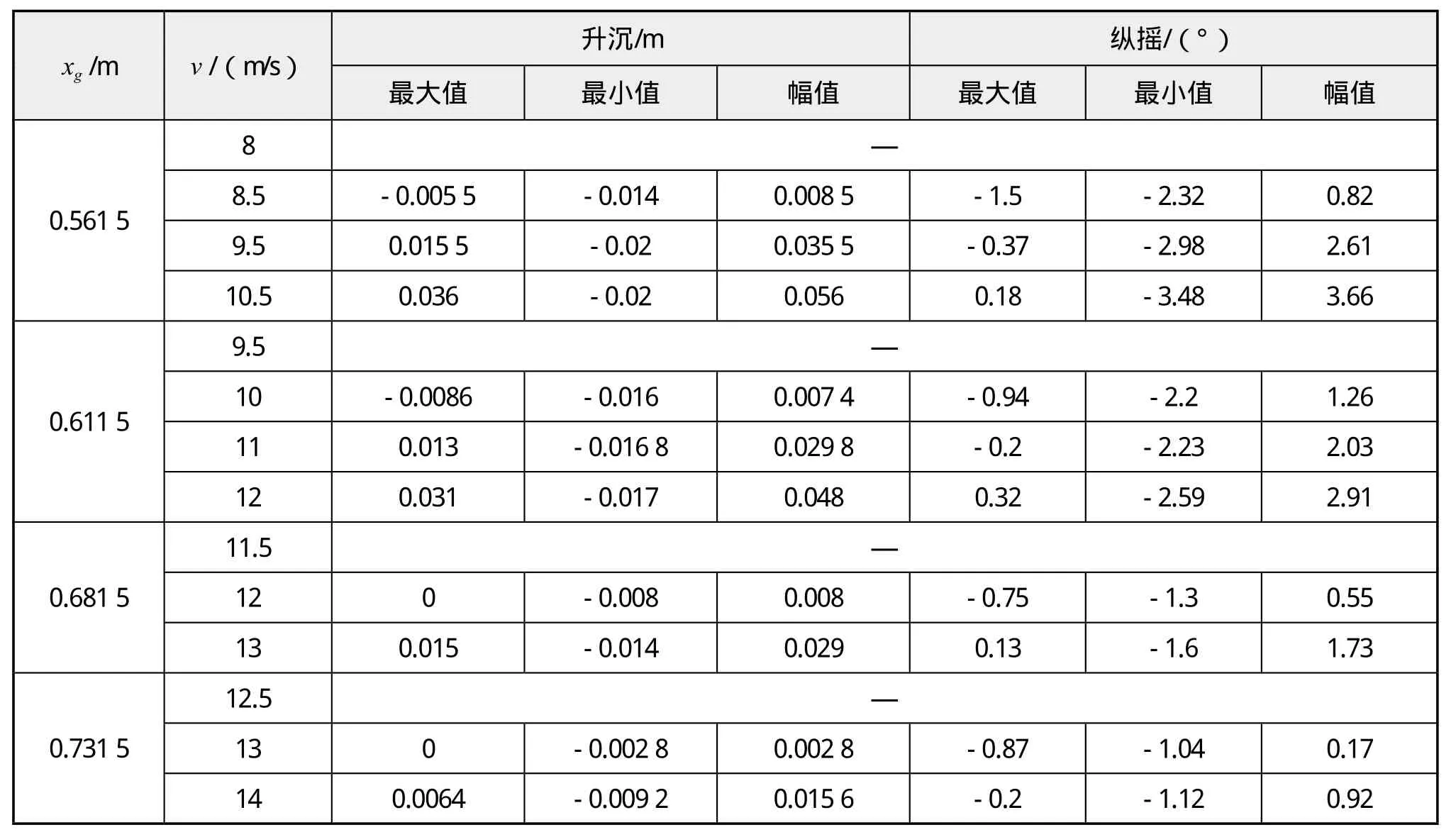
表4 數值計算結果
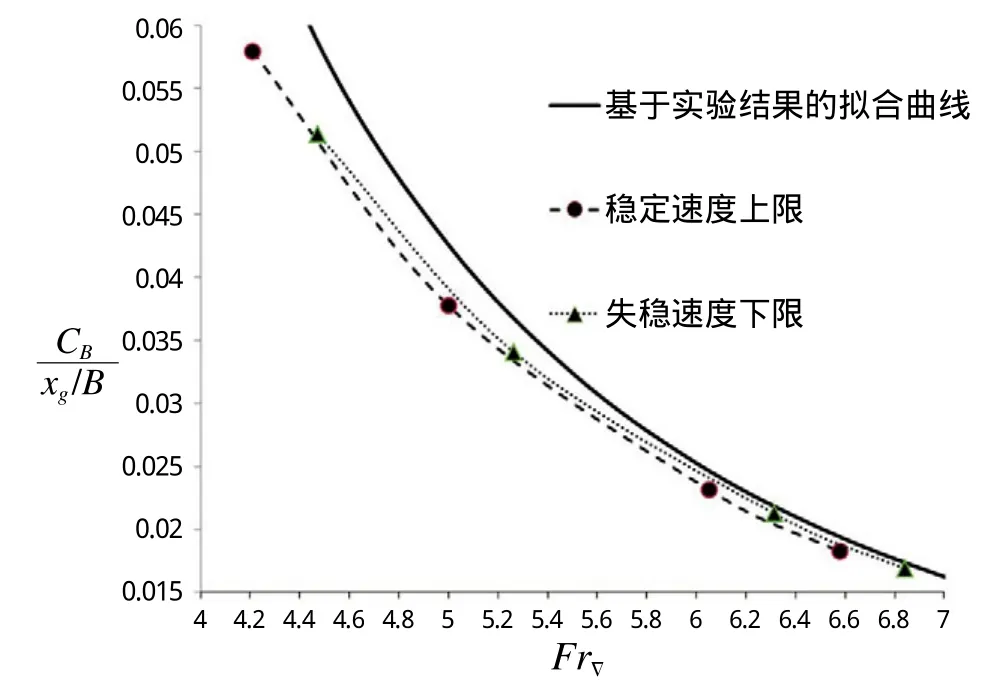
圖7 縱向穩定性界限
如圖7所示,實曲線以上區域為試驗得到的縱向失穩區域(“海豚區”),以下為穩定區,而通過模擬得到的穩定性上限曲線與失穩下限曲線的中間地帶即為縱向運動穩定性界限曲線所在位置。不難看出與實驗值相比較,模擬值的穩定區域較小,失穩區域較大,隨著體積傅汝德數的增加誤差減小,模擬值曲線更加貼近實驗值。
5 結 論
本文運用重疊網格技術對三體滑行艇在高速航行時產生的“海豚運動”進行CFD仿真計算,并結合二分法對縱向穩定性界限進行逼近計算。結果顯示:
(1)隨著重心縱向位置的前移,失穩臨界速度隨之變大,趨勢與試驗結果相吻合。
(2)二分法逼近得到的縱向穩定性界限位于實驗值下方,即失穩區大于實驗結果。
(3)在高傅汝德數條件下,計算結果更加貼近實驗值,誤差極小。
綜上所述,結果顯示文中運用的數值計算方法可以較好實現對三體滑行艇縱向失穩運動的模擬,且失穩速度較為準確,相比于船模試驗具有高效能、低成本等優勢,可為類似船型的設計與優化等工作提供可信的參考數據。
[1] 孫華偉.三體滑行艇船型與阻力性能研究[D].哈爾濱:哈爾濱工程大學,2010:1-51.
[2] Azcueta R,Caponnetto M,Soding H.Planing boats in waves[C]// Proceedings of IWSH’ 2003.Third International Workshop on Ship Hydrodyamics,Wuhan :Wuhan University of Technology Press,2005,2.
[3] 趙發明,高成君,夏瓊.重疊網格在船舶CFD中的應用研究[J].船舶力學,2011(4):332-341.
[4] 田書玲.基于非結構網格方法的重疊網格算法研究[D].南京:南京航空航天大學,2008:56-80.
[5] Thomas P D,Middlecoff J.F.,Direct Control of the Grid Point Distribution in Meshes Generated by Ellipitic Equations[J].AIAA Journal.1980,18 :652-656.
[6] Royk,Bharats,Rajkeshar S A.Comprehensive Generalized Mesh System for CFD Application[J].Mathe and Computers in Simulation,2008,78:605-617.
[7] 鄧銳.阻流板對雙體船水動力性能影響的數值研究[D].哈爾濱:哈爾濱工程大學,2010:31-38.
[8] 趙連恩.高性能船舶水動力原理與設計[M].哈爾濱:哈爾濱工程大學出版社,2007:195-199.
[9] 王慶旭,鄒勁,史圣哲,等.高速型三體滑行艇簡介及縱向穩定性初步研究[A].第十五屆中國海洋(岸)工程學術討論會論文集,2011:226-230.

