振動錘沉樁計算方法

胥新偉，時閩生，劉亞平

（1.中交天津港灣工程研究院有限公司，天津 300222；2.中交第一航務工程局有限公司，天津 300461）

振動錘沉樁計算方法

胥新偉1，時閩生1，劉亞平2

（1.中交天津港灣工程研究院有限公司，天津 300222；2.中交第一航務工程局有限公司，天津 300461）

振動沉樁過程中由于樁周動摩阻力的影響，樁身振動加速度隨著入土深度的增加而逐漸減小，動摩阻力隨著入土深度的增加而逐漸增大，當振動錘激振力能夠克服樁側動摩阻力及端阻力，同時樁端產生的最大振幅能夠克服土處于彈性階段的最大位移后樁可繼續下沉。通過對樁身劃分單元的方法，確定樁側動摩阻力與樁身振動加速度之間的關系，計算得到不同入土深度位置的樁側振動加速度，同時考慮應力波在樁身的傳遞，最終獲得樁在不同時刻的動摩阻力，并通過樁端單元的振動加速度計算得到樁端最大振幅。

振動錘；振動沉樁；動摩阻力；波動方程

0 引言

振動錘沉樁作為一項成熟的技術在國內外應用非常普遍，隨著振動錘技術的發展，振沉能力更高的振動錘及多臺聯動振動錘組的應用成功，使大直徑鋼管樁或鋼圓筒的振動下沉成為現實。然而振動沉樁的理論研究落后于工程實踐[1]。

對于振動沉樁可行性分析，通常在工程經驗的基礎上采用力平衡模型進行分析，例如Jonker提出了β法預測鋼管樁的可打入性公式[2]，β即為管樁內外側阻力的經驗系數。Warrington則根據標貫試驗結果及工程經驗，提出了不同標貫擊數土的動摩阻力。法國PTC公司以及美國ICE公司均在工程經驗的基礎上提出了不同土質的動摩阻力值。

日本建調株式會社介紹了一種計算樁側動摩阻力的方法[3]，利用樁側摩阻力降低系數μ來代表樁側靜摩阻力降低為動摩阻力的程度，認為μ的大小與樁的振動加速度有關，樁身振動加速度越大μ越小，且不同土質擁有不同的最小μ值。本文認為μ除和土質有關，還隨著樁入土深度的增加逐漸增大，通過劃分單元的方法計算得到不同深度處樁側土的μ值，獲得樁側動摩阻力，從而對沉樁可行性進行判斷。

1 動摩阻力的計算

1.1 日本經驗公式

當樁靜止存在于土體中，它與土之間存在著靜摩阻力。通過對樁進行強制振動，樁將振動傳遞給與樁接觸的土壤顆粒使其發生土體液化，造成摩阻力急劇下降[3-4]。以Qsv代表通過振動后降低了的摩阻力，以μ代表摩擦力Qs變為Qsv時的降低系數，Fmax為振動錘最大激振力，則振動沉樁所需滿足的條件如下：

式中：Fmax為振動系統激振力；μ為摩阻力降低系數；Qsv為樁的動摩阻力；Qs為樁的極限靜摩阻力。

μ的大小由振動加速度決定。當振動加速度超過10g以后，即使把振動加速度無限加大，也不會把μ降至0，因此樁的動摩阻力存在一個極限值Qsvmin。

用η表示最大振動加速度與重力加速度的比值，判斷振沉可行性的公式如下：

式中：η為振動加速度比；G0為振動體系重力。

μ=μmin+（1-μmin）e-βη（3）式中：μmin為摩阻力降低系數最小值，該值與土的性質有關，日本經驗推薦：沙質土：μmin=0.15，淤泥質黏土：μmin=0.06，黏土：μmin=0.13；β為與材料有關的比例系數，日本經驗取鋼材的β值為0.52。

根據式（2）及式（3）得到的μ-η關系曲線見圖1。

圖1 μ-η曲線Fig.1 Curve ofμ-η

1.2 公式的改進

1.2.1 樁側動摩阻力計算

在日本經驗公式基礎上，將樁進行單元劃分。假設采用振動錘將長為L的樁沉入土中，入土深度為Z，將樁劃分為n個長度為ΔL的單元組成的模型，如圖2所示。

圖2 振動沉樁計算模型Fig.2 Calculationm odelof vib ration piling

由圖2，假設振動錘及樁組成的振動系統總重力為G0，劃分的每個單元重力為Gi，則有：G0=振動錘的激振力為F。沉入土中的單元，每個單元承擔的動摩阻力為Qsv（ii=1，2，…，n）。單元i在激振力F的作用下的加速度比ηi：

振動沉樁過程中，激振力實際是隨著時間變化的正弦函數，振動錘激振力的表達方式為：

F=Fmaxsin（ωt+φ0） （5）式中：ω為振動錘偏心質量塊旋轉角速度；φ0為振動錘偏心質量塊的初相位角；Fmax為振動錘最大激振力。

假設激振力以沉樁方向為正，拔樁方向為負。當激振力方向為拔樁方向時，取ηi=0，即Qsvi= Qsi，同時考慮應力波在樁身中的傳播速度c=則式（4）可修正為：

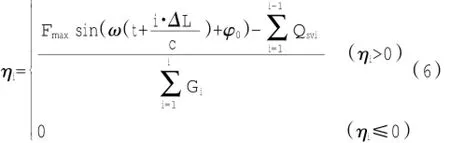
根據式（6）可以求得每個單元的動摩阻力降低系數μi以及相應的Qsvi。

式中：Qsi為單元i承擔的靜摩阻力。

1.2.2 樁端振幅驗算

樁側若產生土體液化，進而由極限靜摩阻力轉化為動摩阻力，則樁身在振動荷載作用下產生的最大位移必須克服土處于彈性階段中的最大位移，否則振幅較小，樁身無法擺脫土壤，就不會有動摩阻力的產生。

樁在振動下沉過程中，首先要將樁端附近的土壤液化，將樁端的極限靜阻力轉化為動摩阻力，因此需要對樁端所產生的最大振幅進行計算。根據式（6），可以求得任一時刻樁端所產生的加速度比ηn，在某一時刻可以使ηn達到最大，得到ηnmax，假設樁端單元n在周期荷載的作用下發生簡諧振動，則振動過程中能產生的最大位移計算公式如下：

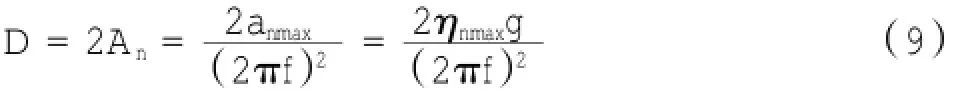
式中：An為樁底部編號為n的單元所產生的最大振幅；anmax為樁底部編號為n的單元所產生的最大振動加速度；f為鋼管樁或鋼圓筒振動主頻率。

2 算例

2.1 鋼圓筒算例

港珠澳大橋東、西人工島島壁結構采用直徑22.0 m的大型鋼圓筒結構組成，利用8臺APE600液壓振動錘聯動的方式振動下沉，最大激振力38 640 kN，振動頻率23.3 Hz。分別于東西人工島選取2個土質相對較好，承載力相對較高的鉆孔資料進行分析。對東西人工島鋼圓筒振動下沉可行性進行計算如表1，得到的振動加速度分布及摩阻力降低系數分布見圖3、圖4。

表1 鋼圓筒計算參數及結果Tab le1 Calcu lating parameter and resultsof steel cylinder

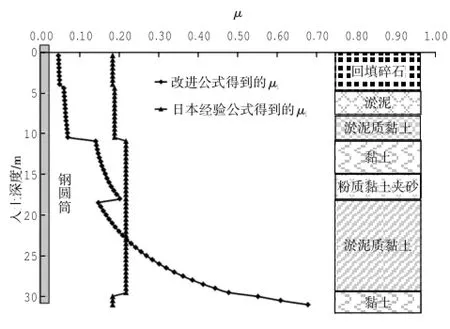
圖3 東人工島μ隨入土深度變化曲線Fig.3 Curve ofμchangesw ith embedded depth of east artificial island

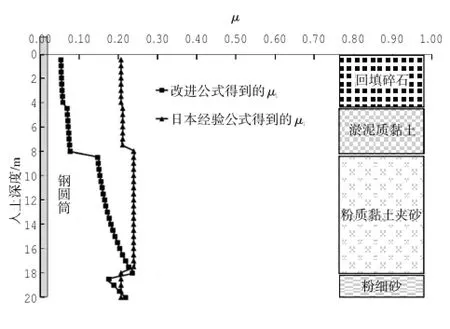
圖4 西人工島μ隨入土深度變化曲線Fig.4 Curveofμchangesw ith embedded depth ofwest artificial island

實際工程中，東人工島鋼圓筒振沉施工過程與西人工島相比，較為困難，自沉完成后振動下沉所需時間較長。西人工島位置的土阻力相對較差，鋼圓筒在自沉完成后很容易振沉到位，振沉時間僅需要幾分鐘便可沉至設計筒底高程。

2.2 大直徑鋼管樁算例

江蘇如東150 MW潮間帶風電場一期示范工程樁基采用1.7 m直徑鋼管樁。振動錘型號DZP500，最大激振力3 000 kN，振動頻率11.3 Hz。根據地質勘查報告對該工程的振動沉樁過程進行分析，計算結果見表2。

經實際工程驗證，實際下沉深度遠不能滿足設計要求，實際下沉深度約為33.0 m。通過改進后的公式對下沉進行驗算，得到的計算結果較接近實際情況。

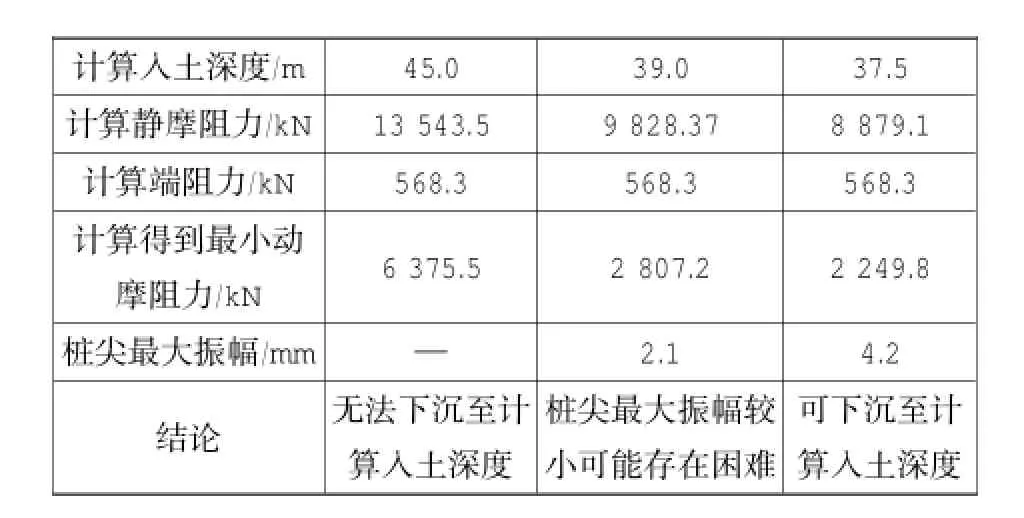
表2 計算結果匯總Table 2 Summ ary of calculation results

3 結語

改進后的計算方法認為樁在動摩阻力的影響下，樁身振動加速度隨著入土深度的增加逐漸減小。通過對樁身劃分單元，求得不同單元動摩阻力隨時間的變化，匯總單元動摩阻力可以得到樁的總動摩阻力隨時間的變化。樁受到動摩阻力的影響樁身的振幅隨著入土深度的增加逐漸減小。假設樁端的振動為簡諧振動，其振幅受到樁端單元振動加速度以及振動頻率的影響。

在進行振動沉樁可行性計算過程中，樁靜土阻力計算的準確性也是尤為重要的，因此在進行振動沉樁可行性分析之前，需要獲得盡可能準確的地質資料，同時在計算樁的靜土阻力過程中，根據樁徑的不同需要對土塞效應、擠土效應以及樁內壁土阻力進行準確的估計[6-7]。

[1]騰云楠，李小彭，楊鐸，等.基于振動沉樁機的振動摩擦系統動力學分析[J].東北大學學報：自然科學版，2010（7）：1015-1018. TENGYun-nan,LIXiao-peng,YANGDuo,etal.Dynamic analysis of vibration-friction system on a vibrating pile driver[J].Journal ofNortheastern University:Natural Science,2010(7):1 015-1 018.

[2]汪金衛，陳福全，簡洪鈺.高頻液壓振動錘打樁的可打入性分析模型[J].福建工程學院學報，2009（1）：9-15. WANG Jin-wei,CHEN Fu-quan,JIAN Hong-yu.Themodels for vibratory drivabilityofpilesby vibratoryhammer[J].Journalof Fujian University of Technology,2009(1):9-15.

[3]王胤.振動打樁機下沉鋼管樁實用計算方法[J].河港工程，1996（3）：11-22. WANGYin.Practical calculationmethod of steel piles drivability by vibratory hammer[J].River and Harbor Engineering,1996(3): 11-22.

[4] 劉寶河，邊強，袁孟全.振動沉樁錘的選型及應用[J].中國港灣建設，2008（3）：38-41. LIU Bao-he,BIAN Qiang,YUAN Meng-quan.Selection and application ofvibratory piling hammers[J].China Harbour Engineering,2008(3):38-41.

[5]謝曉娟.振動沉樁過程中的樁-土相互作用的動力學分析[D].沈陽：東北大學，2010. XIE Xiao-juan.Dynamic analysis of the pile-soil interaction in process of vibratory sinking piles[D].Shenyang:Northeastern University,2010.

[6] 陳波，李向秋，閆澍旺.動力打入鋼管樁中的土塞研究現狀[J].中國海上油氣工程，2003（1）：24-27. CHEN Bo,LIXiang-qiu,YAN Shu-wang.Studies on soil plug in driving open-ended steel pipe pile[J].China Offshore Oiland Gas: Engineering,2003(1):24-27.

[7]劉潤，禚瑞花，閆澍旺.大直徑鋼管樁土塞效應的判斷和沉樁過程分析[J].海洋工程，2005（2）：71-76. LIURun,ZHUORui-hua,YAN Shu-wang.Plug effecton drivability of large-diameter steel piles[J].The Ocean Engineering, 2005(2):71-76.

Calculation method of pile drivability by vibratory hammer

XUXin-wei1,SHIMin-sheng1,LIUYa-ping2
（1.CCCCTianjin PortEngineering Institute Co.,Ltd.,Tianjin300222,China;
2.CCCCFirstHarbor Engineering Co.,Ltd.,Tianjin 300461,China）

While the pile was subsiding,because of the effect of dynam ic friction around piles，the vibratory acceleration of the pilebodywasdecreased along the depth into soil,and the dynamic frictionwas increased along the depth into soil.When the vibratory hammer exciting force is greater than the sum of dynam ic friction and the pile end resistance，and if themax amp litude at the bottom of the pile is greater than the elastic deformation of the soil,the pile could submerge continuously.Through themethod for dividing the pile into unit,we determined the relationship between the friction and acceleration of the pile,calculated the accelerations ofdifferentunit,considered the stresswave passed in piles and then got the dynamic friction of the pile in different time.Themax amp litude at the end of the pile could be obtained by calculating the vibration acceleration of the unit.

vibratory hammer;vibration piling;soil friction force;wave equation

U655.553

A

2095-7874（2015）05-0041-04

10.7640/zggw js201505011

2015-03-05

胥新偉（1981— ），男，河北張家口人，碩士，工程師，結構工程專業。E-mail：xxw.350@163.com