自動裝箱控制系統的設計

周建洪，賈衛東，張玉龍，李澤明

（遼寧科技大學 遼寧 鞍山 114051）

自動裝箱碼垛機械手在現代碼垛包裝線上占有重要的地位，用人工來完成這項工作，存在著勞動強度大、效率低等諸多的弊端，也無法滿足包裝線發展的需求，采用自動化的操作手段已經成為必然的趨勢[1]。自動裝箱碼垛機械手在日本、德國等發達國家在上個世紀九十年代已經在推廣搬運、碼垛的自動化和機器人化方面取得了顯著進展，最近幾年我國的機械手搬運技術取得了突飛猛進的發展，應用十分廣泛[2]。

1 自動裝箱系統的組成及工作原理

現在產品包裝線上的裝箱碼垛作業主要依靠人工搬運來完成，為了節省人力成本，減少勞動強度，提高工作效率，設計了此自動裝箱系統，本設計是針對包裝完畢的小型電器包裝盒進行自動裝箱工作[3]。根據現場的實際需要，自動裝箱系統的機械結構設計示意圖如圖1所示。自動裝箱系統有碼垛機械手部分、包裝盒定位部分、紙箱定位輸送3部分組成。圖中1、2、3、4軸構成了機械手的主體部分，主要實現對包裝盒的抓取、搬運與裝箱等的動作。底座的作用是固定機械手，與地面用螺栓連接，是機械手穩定工作的關鍵。1軸在底座水平方向上做軸向轉動，由伺服電機M1驅動，實現機械手臂朝向運動，使機械手爪運動到包裝盒或紙箱方向。2軸在水平方向做徑向運動，由伺服電機M2驅動，實現機械手臂徑向運動，使機械手夾爪運動到包裝盒或紙箱的中心位置正上方。3軸在豎直方向做高程運動，由伺服電機M3驅動，實現機械手高程直線運動，使機械手爪運動到包裝盒或紙箱位置，抓取或放置包裝盒。4軸在水平方向做軸向運動，由伺服電機M4驅動，實現機械手腕部軸向運動，調整手爪的姿態，以便于準確的抓取和放置包裝盒[4]。

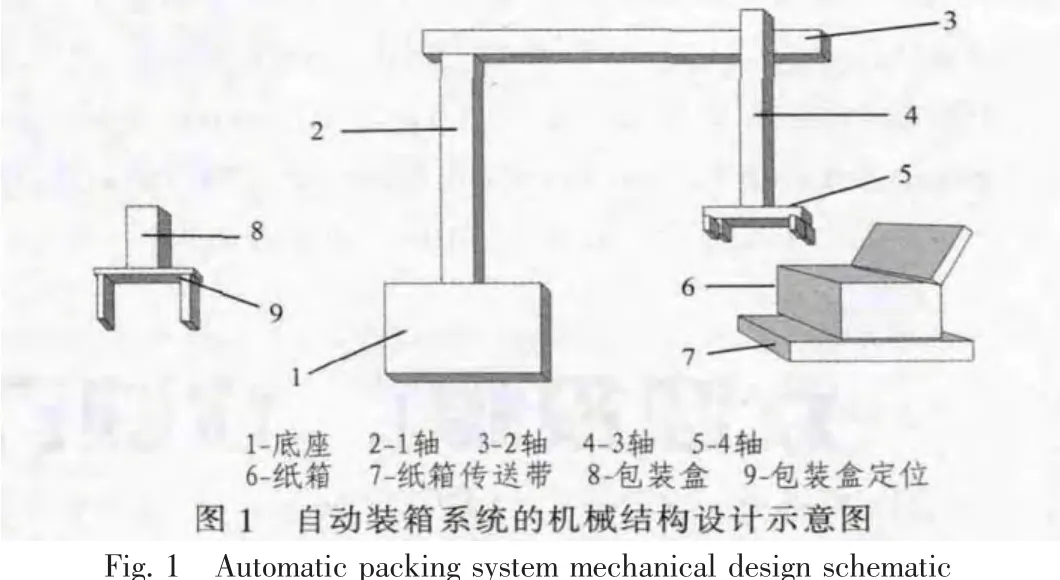
啟動機械手后，當包裝盒定位處的光電開關檢測到有包裝盒，單片機通過USART串口處的條碼掃描儀獲得包裝盒上的條碼信息，記錄下包裝盒的類型；紙箱定位處的光電開關檢測到紙箱定位好時，單片機通過USART串口處的條碼掃描儀獲得紙箱上的條碼信息，記錄下紙箱類型，系統會查表確定裝箱方案。然后機械手運動到包裝盒放置處抓取包裝盒、運送、裝箱，直到箱子裝滿，傳送走后，等待下一個箱子到來繼續裝箱。

2 控制系統硬件電路設計

圖2為控制系統硬件電路原理圖。系統采用STM32F103XX系列單片機作為控制核心，由它通過RS-485總線與伺服電機驅動器進行通訊，從而實現各種機械動作，圖2中1#～4#伺服電機分別對應機械手的四個運動軸電機，由對應的4個伺服驅動器驅動，用于完成對包裝盒的抓取、運送、裝箱等操作。單片機通過IO接口與外部開關量輸入輸出信號相連，開關量輸入部分負責獲取各個機械運動的極限位置信號和各個工位狀態的限位開關信號。包括極限位置的檢測信號，伺服驅動器備妥狀態信號，以及各個工位狀態信號。系統的開關量輸出部分包括夾爪電磁鐵的吸合和松開，以及聲光報警功能的控制。單片機通過USART串口處的條碼掃描儀讀取包裝盒和紙箱上的條碼信息，通過查表確定裝箱方案。工業計算機用來顯示和存取數據，通過RS-232串口通訊與單片機進行通訊。

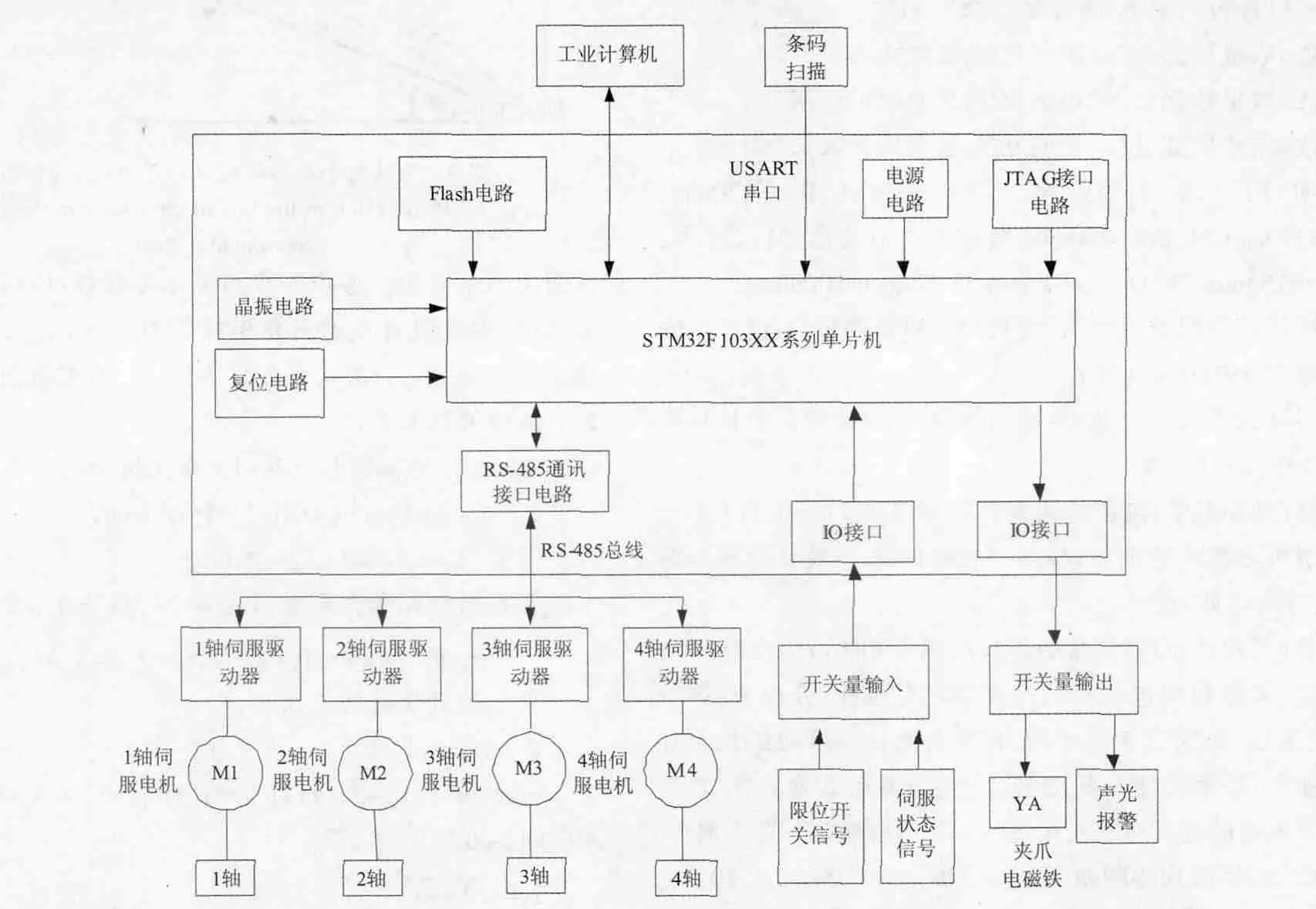
圖2 控制系統硬件電路原理圖Fig.2 Control system hardware circuit diagram

3 控制系統軟件設計

本設計主要完成對小型電器產品包裝盒的抓取和裝箱操作，啟動機械手后，系統開始自檢，自檢完成后，檢測包裝盒是否就位，紙箱就位后記錄紙箱的類型，包裝盒就位后記錄包裝盒的類型，系統查表確定裝箱方案。然后自動裝箱系統完成對包裝盒的抓取、運送、裝箱操作，直到紙箱裝滿，傳送走后，等待下一紙箱到來繼續裝箱[5]。

3.1 紙箱內包裝盒擺放方式的計算

根據任務要求，小型電器產品包裝盒共有3類，1類包裝盒的規格為 155×77×100 mm；2類包裝盒的規格為 150×70×100 mm，3類包裝盒的規格為140×70×100 mm。紙箱共3類，1 號紙箱規格為 470×370×260 mm，2 號紙箱規格為 470×370×360 mm，3號紙箱規格為560×430×350 mm。則裝箱方案如表1所示。

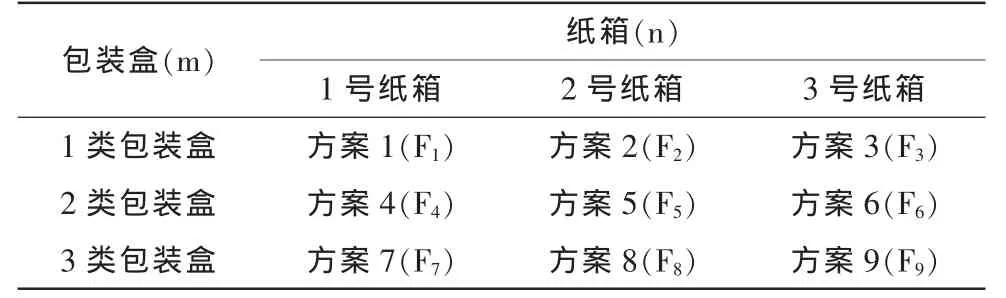
表1 裝箱方案Tab.1 Packing scheme

為了確定每個方案的具體裝箱方案，建立抽象的數學模型，機械手系統為4軸運動系統，建立三維坐標系來表示各個點的位置。坐標中各個點坐標為（θ，r，h），機械手抓的轉動角度設為β，各坐標參量的物理意義如下：

θ：1#軸的相對轉動量，表示機械手朝向運動，其范圍是θ∈（－170°，170°）；

r：2#軸的相對位移量，表示機械手臂展徑向運動，其范圍是 r∈（－50 mm，1050 mm）；

h：3#軸的相對位移量，表示機械手高程直線運動，其范圍是 h∈（－50 mm，550 mm）；

β：4#軸的相對轉動量，表示機械手腕部軸向運動，其范圍是 β∈（－170°，170°）。

已知紙箱左下角一點坐標為 OB（θB，rB，hB），紙箱尺寸為L_Box、W_Box、H_Box，包裝盒工位上的包裝盒中心坐標為OM（θM，rM，hM），包裝盒尺寸為 L_Object、W_Object、H_Object。

計算出每箱的層數，每層的行數和列數。

層數=取整數部分（紙箱的高/包裝盒的高）

行數=取整數部分（紙箱的長/包裝盒的長或寬）

列數=取整數部分（紙箱的寬/包裝盒的寬或長）

例如：F1方案，1號紙箱，其尺寸為：L_Box=470mm、W_Box=370mm、H_Box=260mm；放置1類包裝盒，其尺寸為：L_Object=155mm、W_Object=77mm、H_Object=100mm

該紙箱可以擺放層數為：層數=取整（紙箱的高/包裝盒的高）=取整（260/100）=2（層）

每層可以擺放的行數=取整 （紙箱的長/包裝盒的長）=取整（470/155）=3（行）或

取整（紙箱的長/包裝盒的寬）=取整（470/77）=6（行）

每層可以擺放的列數=取整 （紙箱的寬/包裝盒的寬）=取整（370/77）=4（列）或

取整（紙箱的寬/包裝盒的長）=取整（370/155）=2（列）

所以，該紙箱中包裝盒的擺放方式有兩種，分別為：第一種方案，三層，每層分3行4列，包裝盒的長與紙箱的長所在的直線相平行；第二種方案，三層，每層分6行2列放置，包裝盒的長與紙箱的寬所在直線相平行。我們選擇第一種方案。

因此，相鄰兩列的間距為：dC＝（370－4*77）/5=12.4＞10

相鄰兩行的間距為：dL＝（470－3*165）/4=1.25＜10

當間距dC和dL大于10 mm時，按10 mm計算，當間距小于10 mm時，按實際所求計算，但當間距小于1 mm時，認為方案不成立。

3.2 各包裝盒中心坐標計算算法

計算出包裝盒的擺放方式后，就可以根據其對應關系求得各個包裝盒中心在紙箱內的相對位置，其中紙箱左下角一點 OB（θB，rB，hB）的各個坐標為已知的。 共分為兩層，每一個包裝盒的中心坐標設為 OX（θX，rX，hX），其中 X=12（i－1）+4（j－1）+k，i=1，2 表示層數，j=1，2，3 表示行數，k=1，2，3，4，表示列數。 因此 OX也可以表示為 O（i，j，k），其坐標表示為（θ（i，j，k），r（i，j，k），h（i，j，k）），機械手爪轉角為 β（i，j，k）。 根據包裝盒在紙箱內擺放 的 方 式 可 知 ，h（i+1，j，k）=h（i，j，k）－H_Object，θ（s+1，j，k）=θ（i，j，k），r（i+1，j，k）=r（i，j，k），β（i+1，j，k）+12=β（i，j，k）。 在 同 層 中 任 意 兩 包 裝 盒 的 中 心 坐標，都有：h（i，j1，k1）=h（i，j2，k2）。

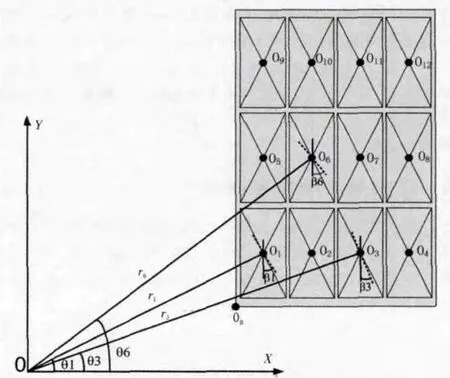
圖3 包裝盒中心在機械坐標系內的平面示意圖Fig.3 Plan sketch of the box in the center of the machine coordinate system

包裝盒中心在機械坐標系內的平面示意圖如圖3所示，從圖中不難看出，各點的直角坐標關系都可以從OB坐標推導 而 得 ，因 此 設 各 點 的 直 角 坐 標 為 O（i，j，k）（X（i，j，k），Y（i，j，k）），它 的極坐標就是 O（i，j，k）（θ（i，j，k），r（i，j，k）），同時設 OB的直角坐標為（XB，YB），具體關系如下：

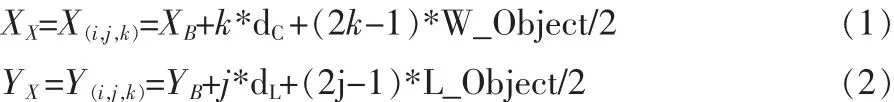
其中：XB=rB*cosθB，YB=rB*sinθB

根據極坐標和直角坐標之間的轉換關系，求得：

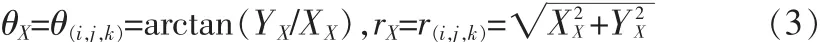
最后整理變換公式如下：

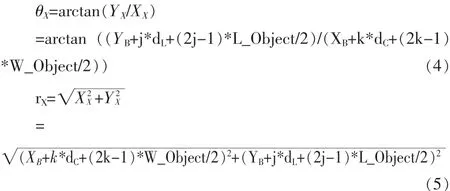
而從圖 3 中可知，4# 軸伺服電機的轉角 β（i，j，k）與 1# 軸伺服電機的轉角 θ（i，j，k）相等。 這里認為當 4# 軸使得機械手爪與臂展 r垂直時，其 β（i，j，k）=0，那么不難求出：β（i，j，k）=θ（i，j，k）

至此，我們可以通過已知的OB點坐標，以及紙箱、包裝盒的尺寸，計算出將要擺放到紙箱內的每一包裝盒的中心OX的坐標。

例如方案 F1，已知 OB在 XY 坐標系中的坐標 OB（XB，YB）為 OB（365，350），hB=780 mm， 則 OB（θB，rB，hB） 為 （43.80°，505.69，780），由于第一層和第二層包裝盒的中心坐標除了高度 h（i+1，j，k）=h（i，j，k）－H_Object 外 ，θ（i+1，j，k）=θ（i，j，k），r（i+1，j，k）=r（i，j，k）， 機 械手爪的旋轉角度 β（i，j，k）=θ（i，j，k），表 2 中只列出第一層各個點的中心坐標，其余方案中包裝盒的中心坐標也是按照此方法計算[6]，則方案F1中裝有包裝盒的紙箱內第一層各點中心位置的坐標如表2所示。

3.3 自動裝箱控制系統程序設計

當計算出了紙箱內各個包裝盒將要擺放的位置的坐標之后，對機械手的運動控制策略也就迎刃而解了。首先機械手裝箱的流程如下。

表2 方案1紙箱內第一層各點中心位置的坐標Tab.2 Cartons each point center position coordinates of the first layer in Plan 1

1）啟動機械手后，系統自檢，機械手復歸到起點（機械零點或任意已知的初始位置）

2）機械手運動到 OM（θM，rM，hM）點抓取包裝盒；

3）機械手運送包裝盒到紙箱內指定的包裝盒位置裝箱；

4）判斷紙箱是否已經裝滿，如未滿，則重復 2）、3），直至紙箱裝滿。

5）裝箱完畢，運走紙箱，等待裝下一箱。

在這個過程中，每一次運動都是從一個已知點運動到下一個已知點，比如從取包裝盒點

OM（θM，rM，hM）運動到 OX（θX，rX，hX），只需要計算各個坐標的差，就可以得到對應軸的相對位移量，如 ΔθX=θX-θM，為 1#軸的相對轉動速度，Δr=rX-rM為2#軸的相對位移。同理，當機械手臂需要從 OX點再到 OM點抓取時，Δθ=θM-θX為 1#軸的相對轉動角度，只是此時的方向與原來相反而已。因此，機械手的運動路徑其實就是計算每次運動的偏移向量Offset（Δθ，Δr，Δh），程序流程圖如圖 4 所示。

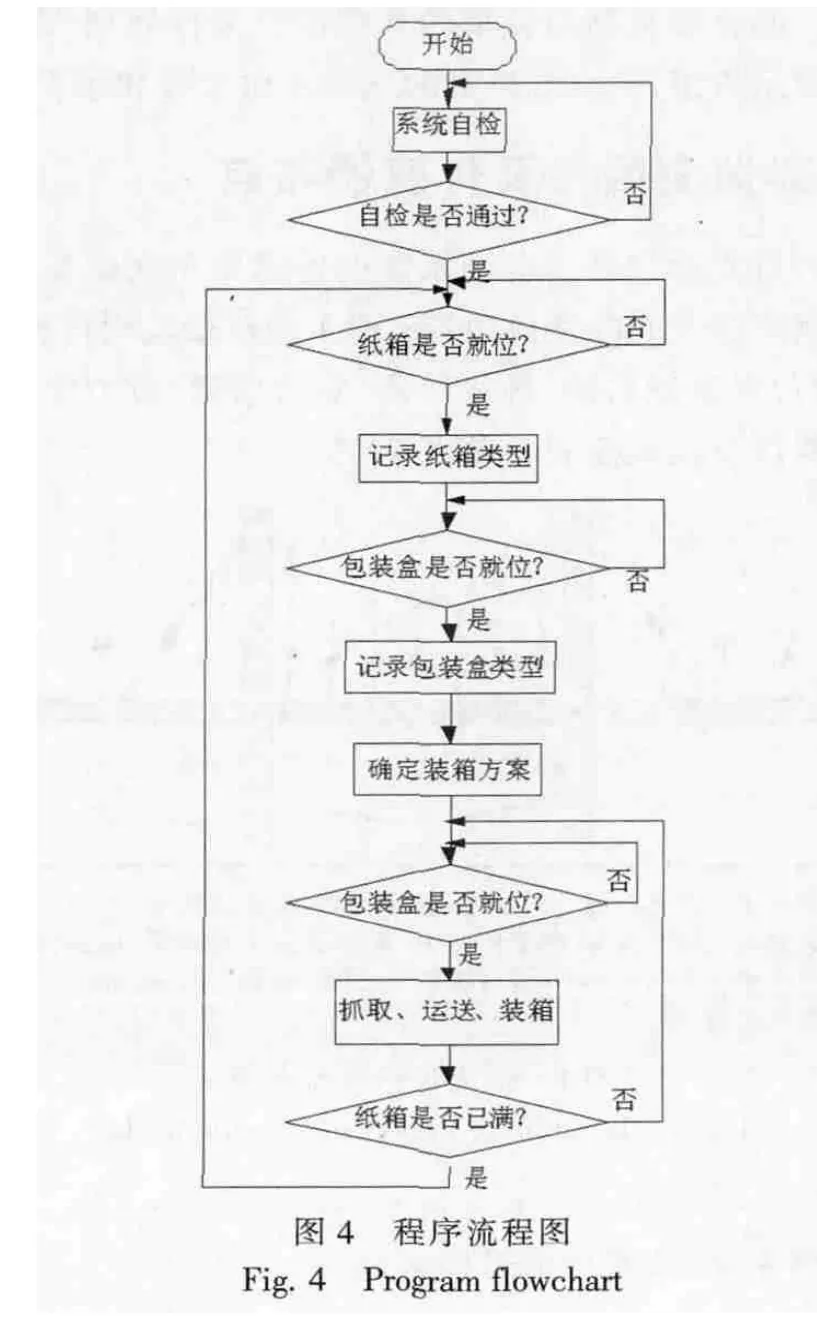
4 結 論

本文是針對某小型電器產品生產企業生產線的實際需求，設計了一個自動裝箱系統，該自動裝箱系統機械結構設計合理，是針對生產線上電器產品的包裝盒，實現自動裝箱系統機械手抓取、運送、裝箱的功能。本自動裝箱系統還可以用于對藥盒、食品盒、塑料盒等的搬運碼垛，因此本設計研究的自動裝箱系統還可以廣泛應用于物流自動化行業中的物料搬運、碼垛等領域，具有廣闊的市場前景。

[1]周鵬云.機械手碼垛技術在大米加工企業中的應用[J].糧食與飼料工業，2011（1）:8-11.ZHOU Peng-yun.Robotic palletizing technology applications in rice processing enterprises[J].Food and Feed Industry，2011（1）:8-11.

[2]張有良.碼垛機械手的設計及電氣控制[J].包裝與食品機械，2007，25（5）:23-25，36.ZHANG You-liang.Palletizing robot design and electrical control[J].Packagingand Food Machinery，2007，25（5）:23-25，36.

[3]馬綱，王之櫟，韓元松.一種新型搬運碼垛機械手的設計[J].機械設計與制造，2000，8（4）:26-27.MA Gang，WANG Zhi-li，HAN Yuan-song.A new handling palletizing robot design[J].Mechanical Design Andmanufacturing，2000，8（4）:26-27.

[4]毛立民，鄒劍.關節型碼垛機械手運動學分析及仿真[J].組合機床與自動化加工技術，2010，9（8）:44-47.MAO Li-min，ZOU Jian.Articulated palletizing robot kinematics analysis and simulation[J].Modular Machine Tool&Automatic Manufacturing Technique，2010，9（8）:44-47.

[5]張敏，石秀華，杜向黨，等.三自由度機械手運動學分析[J].機械與電子，2005（1）:65-67.ZHANG Min，SHI Xiu-hua，DU Xxiang-dang，et al.Three degrees of freedom manipulator kinematics analysis[J].Fourth Edition.Mechanical and Electronic，2005（1）:64-67.

[6]李成偉，朱秀麗，贠超.碼垛機器人機構設計與控制系統研究[J].機電工程，2008，25（12）:81-85 LI Cheng-wei，ZHU Xiu-li，DAI Chao.Palletizing robot mechanism design and control system research[J].Mechanical Engineering，2008，25（12）:81-85.