一維熱方程邊界值識別問題的一種優化算法

李昭敏/武漢東湖學院基礎課部數學教研室

一維熱方程邊界值識別問題的一種優化算法

李昭敏/武漢東湖學院基礎課部數學教研室

本文主要研究了一維熱方程邊界值識別問題。該問題在工業中有很廣泛的應用，對這類問題的研究方法已有很多。本文主要是用一種新的方法——遺傳算法來求解反演邊界值問題。首先將本問題轉化為一個最優化問題，然后通過遺傳算子即交叉算子和變異算子的作用來計算此最優化問題。遺傳算法是一種智能算法，它的應用非常廣泛。到目前為止，已經有很多文獻研究了遺傳算法的全局收斂性。它比一般的優化算法具有更高的收斂速度。本文通過數值例子驗證了遺傳算法在解決熱方程邊界值問題中的有效性。

反邊界值問題； 不適定問題；遺傳算法；遺傳算子

一、引言

數學物理反問題的簡介

在應用數學研究日常生活中具體的自然現象和自然規律時，我們首先要給出自然現象或物理現象的數學描述，即數學模型。而是正確的模型應具備一下三個條件：（1）該模型的解是存在的，即該模型確實時描述了一類自然現象或規律；（2）該模型的解是唯一的；（3）該模型的解對輸入數據是穩定的，即解對數據的誤差是連續的。這也是數學模型必需具備的三個條件，也是我們經常提及到的解的存在性、唯一性和穩定性。若這三個條件中的任何一個不滿足，我們都稱此問題是不適定問題。隨著科學技術的不斷發展，這類不適定問題在實際應用中出現的越來越多，我們把這類不適定問題稱之為數學物理反問題。在很多應用領域都出現了這類反問題。像在資源勘探，大氣測量，海洋工程，遙感技術，控制與識別等領域中出現了大量的反問題。這引起了數學家的廣泛重視和深入研究。使數學物理反問題的研究越來越受到很多人的關注，也使它稱為現代數學領域中發展最快的方向之一。

遺傳算法簡介：

遺傳算法是根據自然界中的生物對其生存的環境根據自己的適應性選擇適合自己的生存環境，特別是在各物種相互競爭的環境中生存。根據達爾文的自然選擇和孟德爾遺傳變異理論，通過生物的繁殖、變異、競爭和選擇等基本形式來實現，使適應環境的變異個體留下來，不適應環境的變異個體被淘汰，通過一代代生物對生存環境的選擇作用，物種變異被定向為向著適應環境的方向發展，最后演變為適應環境的個體，遺傳算法是建立在模擬生物進化過程的基礎上的隨機搜索的優化算法，

在最優化方面的應用就是根據上面的原理，將所求問題轉化為一個優化問題，即確定目標函數。經過一系列的編碼、遺傳、變異、交叉、選擇和解碼等操作，然后利用“適者生存，優勝劣汰”的原理得到問題的近似最優解或最優解。

二、問題描述

本文考慮一下熱傳導問題

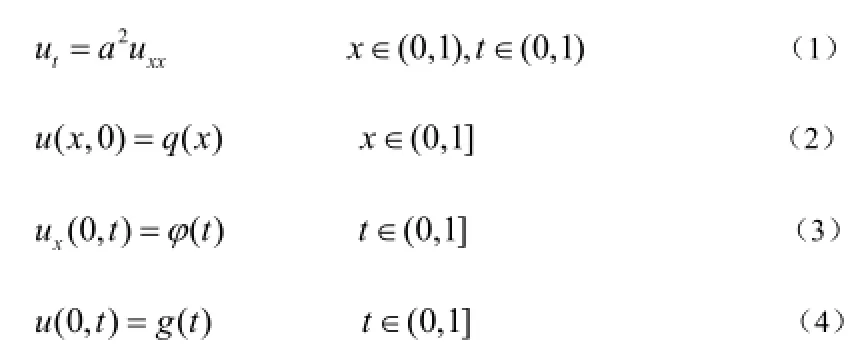
為了求解該問題，本文將用遺傳算法來求解，按照遺傳算法的要求，先將所求問題轉化為一個優化問題即

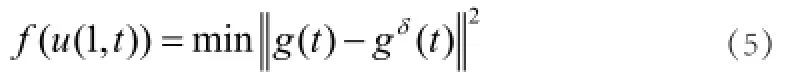
其中上式中大范數為L2范數。G(t)是對應隨機產生的u(1,t)解正問題邊界x=0時的溫度的計算值。gδ(t)是邊界x=0時解正問題時得到的溫度計算值。

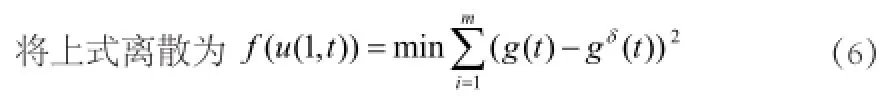
其中m為時間的節點數。

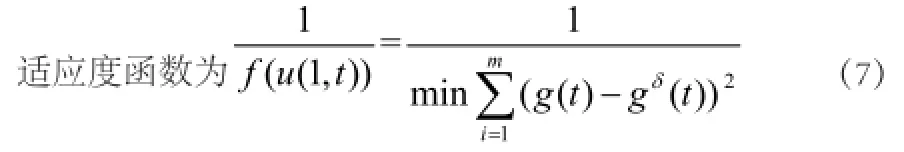
下面將按照上面介紹的遺傳算法來求解該問題。其具體步驟如下：

（1）首先產生一個初始種群u(1,t)，初始種群的大小設置為20.

（2）將產生的初始種群帶入到目標函數（6）中，看是否滿足目標函數的精度要求，若滿足則停止計算，否則進行遺傳操作。

（3）將產生的初始種群帶入到適應度函數（7）中，計算每個個體的適應度值，然后根據輪盤賭方法選擇優良個體。

（4）利用實數編碼的交叉算子和變異算子對所選個體進行變異操作產生新個體，新個體產生后轉入（2）計算。

反復操作以上步驟，直到找到所需要的解為止。

三、數值試驗

本文將通過數值例子來驗證用遺傳算法在求解這類問題時是有效的。

在下面所給的例子中，方程（1）中的a2=1。所得的測量數據是帶有誤差的數據。

例1：已知精確解 u(x,t)=1+2x （8）

則邊界x=1上的溫度為u(1,t)=3此時邊界溫度是一個關于時間t的常熟函數。均可有精確解得到。當分別給加上δ=0.001,0.01,0.05時的擾動量時反演數值結果見圖（1）.從圖中可以看出隨著擾動量的增加實驗結果與精確解之間的偏差越來越大。遺傳算法關于時間t的常數函數是有效的。

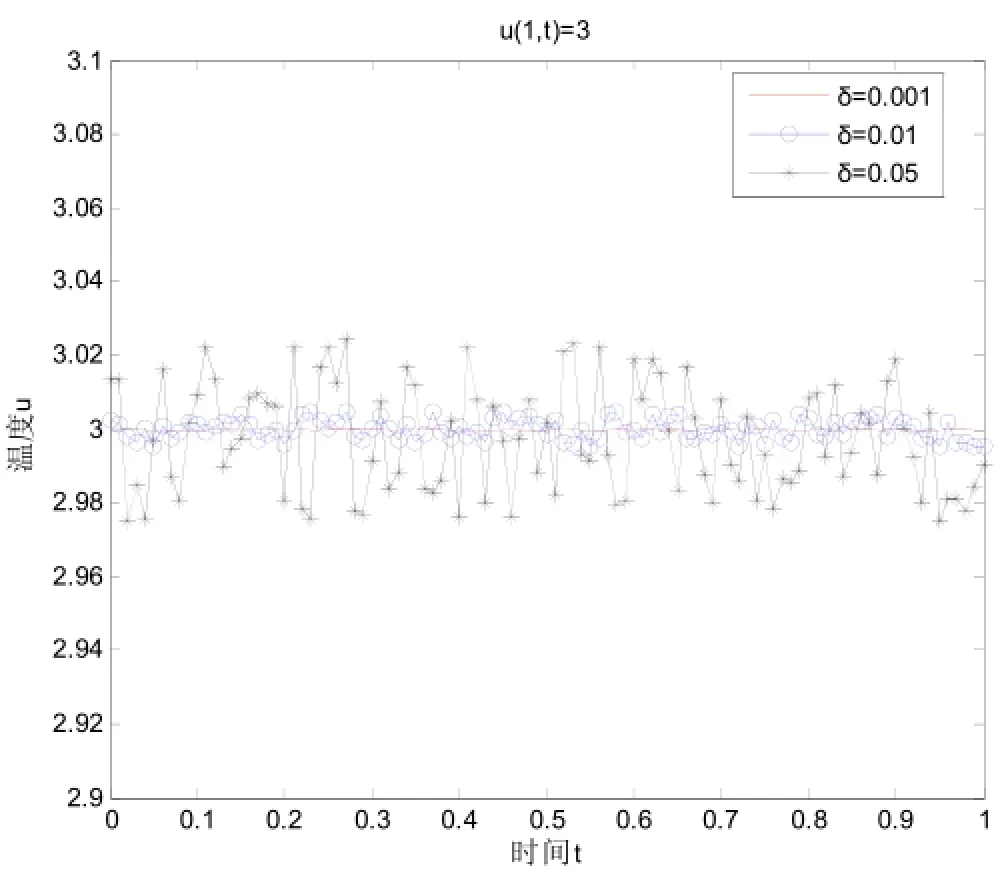
圖1

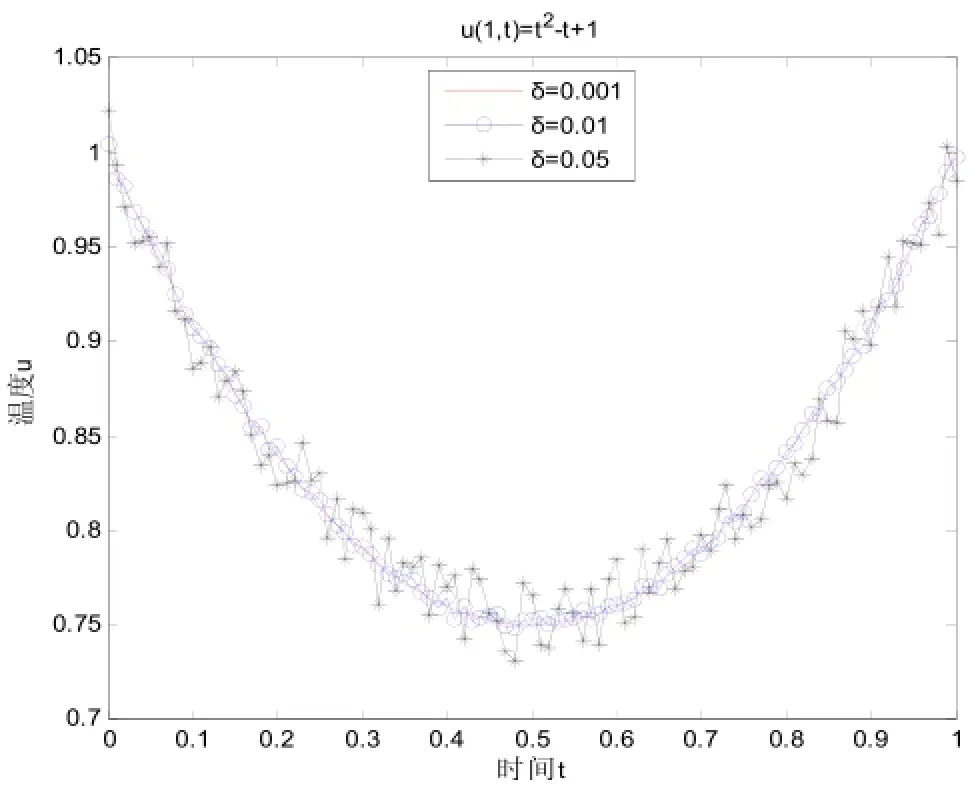
圖2

例3：：假設邊界溫度是由分段函數給出的

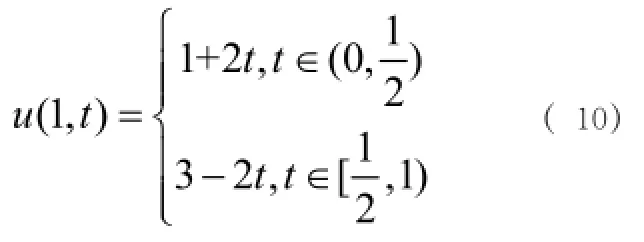
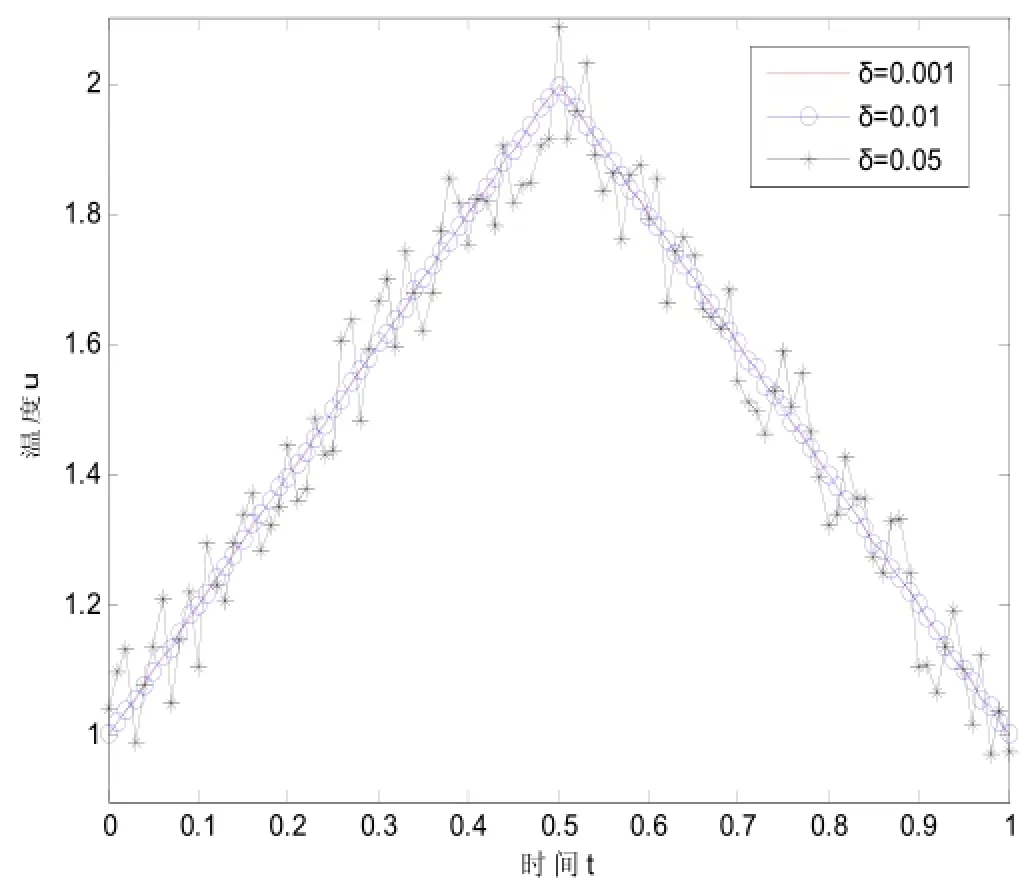
圖3

則邊界給出 ，在邊界x=0時的溫度g(t)由解正問題得到。利用例2的方法可以得到。從圖（3）中可以看出隨著擾動量的增加實驗結果與精確解之間的偏差越來越大。遺傳算法關于時間t的分段函數是有效的，只是在t=0.5時的結果相對差些，其他點與精確解基本吻合。

四、結論

本文中，我們分別研究了邊界值關于時間t的不同函數的識別問題，在數值實驗時，我們分別加上不同的誤差水平，都得到合理的數值結果。也驗證了遺傳算法對邊界值反演問題是有效的。

[1]姜禮尚，陳亞浙等。數學物理方程講義（第二版）；北京：高等教育出版社，1996.

[2]劉繼軍。不適定問題的正則化方法及應用。北京：科學出版社，2005.

[3]肖庭亭，于慎根，王彥飛。反問題的數值解法。北京：科學出版社，2003.

[4] N. Ansari, E. Hou, Computational intelligence for optimization, KluwerAcademic,1997.

[5] C. Bierwirth, D. Mattfeld, Production scheduling and rescheduling with genetic algorithms, Evolutionary computation 7 (1) (1999) 1-17.