不同截面形式鋼桁架承載能力分析

張 懿 婷

(東北林業大學，黑龍江 哈爾濱 150040)

不同截面形式鋼桁架承載能力分析

張 懿 婷

(東北林業大學，黑龍江 哈爾濱 150040)

為研究不同截面形式對鋼桁架承載能力的影響，根據重力相等原則，運用ANSYS對空心圓形、空心矩形以及工字形三種截面形式鋼桁架進行有限元分析，并得到了不同截面形式的鋼桁架應力以及變形規律，指出不同截面形式下的鋼桁架結構的承載能力有很大的差異。

鋼桁架，截面形式，結構應力，結構變形

0 引言

鋼桁架梁由于其充分發揮鋼材的拉力以及壓力，能夠節省材料，減輕結構自重等特點，因此被廣泛用于工業建筑的屋架，橋梁以及輸電塔當中。因此對鋼桁架的承載能力研究是十分重要的。本文立足于探討不同截面形式對鋼桁架結構承載能力的影響，研究了鋼桁架在圓形、空心矩形以及工字形三種截面形式下的應力以及變形的不同，并通過鋼桁架的位移云圖以及應力云圖中得到了相關承載能力。

1 有限元模型

對鋼桁架結構進行有限元分析，首先應該建立精確的有限元計算模型。本文以一個跨度為10 m的鋼桁架結構為例，結構梁高1.5 m，主要由上弦桿、斜腹桿以及下弦桿構成，結構的材料為鋼材，設置相應的材料參數，其中彈性模量為210 GPa，泊松比為0.27，鋼材密度設置為7 850 kg/m3，鋼桁架結構所用單元為材料庫中的Beam189。對于結構橫截面，為了消除自重作用對最后承載能力的影響，采用重力相等原則，設置三種橫截面，分別為空心圓形截面、空心矩形截面以及工字形截面，其中空心圓形的內徑為8 cm，外徑為10 cm；空心正方形的外徑10 cm，內徑8.47 cm；工字形截面的翼板長10 cm，厚1 cm，腹板長8.26 cm，厚1 cm。本例采用由下至上的建模方式，建立的有限元模型以及相關節點號如圖1所示。

建立好鋼桁架結構的有限元模型后，需要對模型進行網格化劃分并且施加邊界條件約束。本例結構對其做簡支鋼桁架梁處理，

對整體結構施加重力作用，并在8～10節點上施加3 000 N向下的集中荷載。

2 不同截面鋼桁架結構應力分析

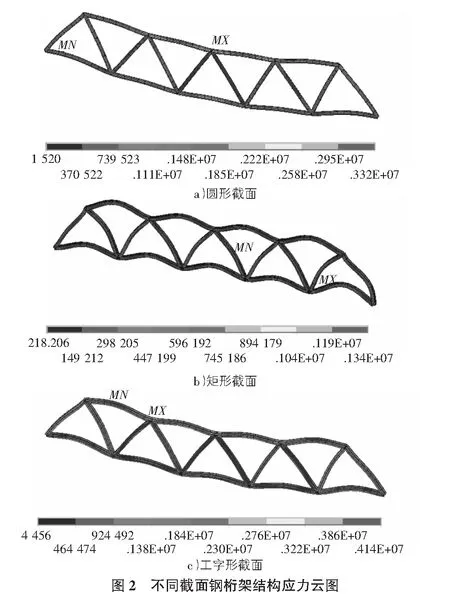
通過對所建立的有限元模型進行加載，加載以后可以得到鋼桁架結構的應力以及變形情況，對結構求解以后可以通過通用后處理中看到不同截面鋼桁架應力云圖如圖2所示。

根據圖2可以看出，鋼桁架結構在不同的截面形式下的應力云圖差別較為巨大，由于結構為對稱型結構，因此應力云圖也基本呈現出對稱型。其中圓形截面桁架結構以及工字形截面桁架結構的應力分布不太均勻，矩形截面桁架結構各個桿件的應力分布較為均勻。對于圓形截面桁架結構，應力最大值出現在對稱軸中點的上弦桿節點處，產生的最大應力為1.33 MPa，最小應力值產生在支點附近，產生的最小應力為1 520 Pa；空心矩形截面桁架結構的應力最大值出現在11節點處，最大應力值為1.13 MPa，應力最小點出現在6節點與10節點之間的斜腹桿處，最小應力值為218.2 Pa；對于工字形截面桁架結構，其應力最大值出現在5節點處，最大應力值為4.14 MPa，最小應力值出現在3節點與5節點之間的上弦桿處，產生的應力值為4 456 Pa。

3 不同截面鋼桁架結構變形分析

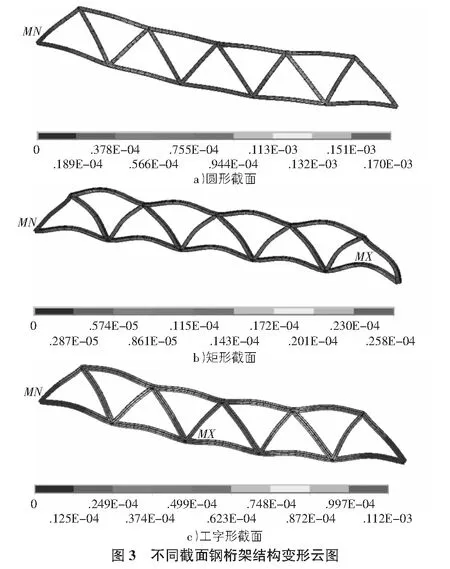
對鋼桁架結構進行求解后，通過通用后處理對鋼桁架結構有限元模型進行查看，所得到的結構變形云圖如圖3所示。

從圖3可以得到不同截面的鋼桁架結構變形特性，三種不同截面形式的鋼桁架結構的變形有較大的差距，結構變形均為對稱型變形，由于結構施加了簡支梁的約束，因此三種截面的鋼桁架變形的最小值均在支點處，變形量為零。空心圓形截面桁架結構與空心矩形截面桁架結構的變形云圖較為相似，并且變形分布很不均勻，其中處于靠近軸中心桿件與節點的變形量較大，處于支點附近的桿件與節點的應力變形較小。圓形截面桁架結構的最大變形處于軸中心的6節點處，最大變形值為1.7 cm，工字形截面桁架結構的最大變形值出現在9節點處，最大變形值為1.12 cm；根據空心矩形結構桁架結構的變形云圖可以看出，此種結構的各桿件變形分布較為均勻，變形較大的點主要出現在上、下弦桿的跨中處，其中最大變形值出現在2節點與11節點的下弦桿跨中處，出現的最大變形值為0.258 cm。

4 結語

通過有限元計算軟件ANSYS對空心圓形、空心矩形以及工字形三種不同截面的鋼桁架結構進行有限元分析，根據計算得到的應

力云圖以及位移云圖可以看出三種結構的承載能力有較大的差異。其中圓形截面結構和工字形截面結構的應力以及變形分布很不均勻，矩形截面結構的應力以及變形分布相對均勻。三種截面的應力極值大小順序為：工字形截面>圓形截面>矩形截面，矩形截面的應力極值要遠小于其余兩種截面；其中三種截面的變形極值大小順序為：圓形截面>工字形截面>矩形截面，矩形截面結構的變形極值較其余兩種截面結構形式的變形極值要小得多。

鋼桁架結構在工程中發生破壞的原因除了承載能力不足以外，還與其動力特性、溫度應力，設計合理性以及施工技術的成熟性有關，在實際設計和施工中應當加以注意。

[1] 王 洋,郝志軍.ANSYS在土木工程應用實例.北京：中國水利水電出版社,2010.

[2] 李眾徹，孟慶超，何鈺龍，等.溫度變化對人字形鋼桁架的應力及變形分析.建材發展導向，2014(2)：78-79.

[3] 朱志斌.某工程大型鋼桁架節點試驗與分析.安徽建筑,2015(3):215-216.

[4] 蘭盛磊.基于SAP2000的轉換桁架的鋼節點有限元分析.四川建材,2015(4):35-36，39.

[5] 王洪濤.高強鋼—混凝土組合梁靜力性能研究.北京：北京工業大學,2013.

Analysis of bearing capacity of steel truss in different section

Zhang Yiting

(NortheastForestryUniversity,Harbin150040,China)

In order to study the influence of different section forms on the steel truss bearing capacity, according to the principle of equal gravity, using ANSYS of hollow circular, rectangular hollow and the Ⅰ-shaped three section of a steel truss by finite element analysis, and get different section forms of steel truss stress and deformation, points out that the different section forms of steel truss structure bearing capacity has great difference.

steel truss， cross section form， structural stress, structural distortion

2015-09-13

張懿婷(1995- )，女，在讀本科生

1009-6825(2015)33-0052-02

TU312

A